Couleur science
La science de la nature pour les curieux Voir les Non lu | Plus vieux en premierComment fonctionnent les cierges magiques ?
Couleur science par Anonyme le 01/01/2026 à 05:21:00 - Favoriser (lu/non lu)

Parmi les quelques composés pyrotechniques d’intérieurs qui existent, figurent les cierges magiques. Ce sont des petites tiges que l’on enflamme comme une bougie, et cela produit ensuite des étincelles jaillissant sur les côtés. L’ensemble est sans réel danger : les étincelles ne brûlent pas, bien qu’une fois consumée, la tige métallique qui subsiste reste très chaude, chauffée au rouge en réalité.
Dans cet article on va voir la science qui se cache dans ces petits accessoires utilisées lors des fêtes.
Les cierges magiques sont constitués de plusieurs ingrédients responsables de la combustion et de la production d’étincelles :
- Un combustible : généralement de la poudre de charbon, de l’amidon, ou un sucre (dextrose, glucose).
- Un oxydant : habituellement du salpêtre (ou nitrate de potassium).
- Les composés métalliques responsables de la production d’étincelles : typiquement de l’aluminium, du magnésium, du titane ou du fer en poudre fine.
Ces ingrédients sont mélangés au sein d’une pâte, qui est ensuite enrobée autour d’une tige métallique puis séchée.
Lorsque l’on allume le cierge magique, le combustible et l’oxydant vont réagir. L’oxygène provient de l’oxydant et pas de l’air comme pour une bougie. Ceci favorise la combustion, car tous les ingrédients sont déjà en place. Et comme il n’y a pas besoin d’air, ils pourraient fonctionner sous l’eau (comme une arme à feu peut elle aussi fonctionner sous l’eau).
Durant cette combustion, les particules métalliques sont également enflammées. Ces dernières brillent très vivement : ce sont les étincelles. En général, on utilise des particules d’aluminium ou de magnésium pour les étincelles blanches et brillantes, et du fer pour celles qui sont plus orangées. D’autres couleurs peuvent être obtenues avec d’autres métaux : bleu-vert avec le cuivre, vert avec du baryum, violet avec du potassium…
Ce sont les mêmes que pour les feux d’artifices.
Les étincelles jaillissent à cause de la combustion très rapide qui provoque de micro-explosions en projettent ces particules tout autour. C’est aussi ce qui donne son bruit de crépitement.
Ces particules sont très fines : des poussières. Elles atteignent 1 000 à 1 500 °C, ce qui les rend visibles. Mais tout comme une étincelle d’une meuleuse par exemple, elles ne sont pas douloureuses sur la peau : leur température est peut-être très élevée, mais la chaleur qu’elles véhiculent (soit l’énergie thermique) est très faible à cause de leur petite taille.
Ces étincelles sont donc un autre exemple pour mettre en évidence la différence entre chaleur et température.
Il faut toutefois faire attention à ne pas les tenir trop près du visage, car elles peuvent toujours endommager les yeux.
En somme, ces cierges magiques sont de mini feux d’artifices et en comportent toutes les particularités chimiques : la présence d’un oxydant directement dans le matériau combustible (pour favoriser la combustion), et des inclusions de métaux pour produire des étincelles ou des flammes colorées !
Comment fonctionne une gomme ?
Couleur science par Anonyme le 04/12/2025 à 05:59:00 - Favoriser (lu/non lu)

On les utilise depuis la plus petite école, mais sait-on vraiment comment elles marchent ? Je parle des gommes, celles utilisées pour effacer du crayon à papier, et parfois du stylo.
Je distinguerais ici essentiellement trois techniques utilisées par les gommes pour effacer.
Les gommes tendres
La première méthode, est probablement la plus commune. Si l’on prend une gomme blanche, ou bien la partie rose des gommes mi-roses, mi-bleues bien connues, alors on a à faire à une matière souple et caoutchouteuse. Littéralement de la gomme.
Pour le crayon à papier, le fonctionnement d’une gomme en lui-même est lié au fonctionnement du crayon.
Une mine d’un crayon à papier est formé essentiellement de graphite, d’argile, et d’un liant plus ou moins gras. Plus il y a d’argile, plus la mine est claire et « grasse ». Le taux d’argile est alors soit haut, soit bas, sur une échelle qui a donné la nomenclature avec H/B (pour haut et bas : un 10H est fort en argile, fiable en graphite, clair et gras, alors qu’un 10B est au contraire riche en graphite, sombre et dur — le HB est au milieu).
Lors d’un tracé, la mine s’use sur le papier et se fixe dans les aspérités de ce dernier. La liaison entre le papier et la mine est essentiellement mécanique pour ce qui est des mines dures (donc « xB »). Pour les mines grasses, riches en argile et en liant, la mine subsiste aussi sur le papier par des liaisons moléculaires (forces de van der Waals…).
Une gomme blanche ou rose « caoutchouteuse » est à la fois poreuse et adhérente. Plus que le papier, en vérité. Grâce à cela, lorsque l’on frotte la gomme sur un dessin au crayon, le graphite se détache du papier et se colle alors à la gomme. La gomme, elle, est suffisamment tendre pour produire des sortes de « copeaux ». Ces copeaux sont alors éliminés avec le graphite collé dessus et la gomme reste propre, mais elle finit par s’user.
Ajoutons qu’avant l’invention de ces gommes, c’était de la mie de pain qui était utilisée pour retirer les traits du crayon. Et avant l’invention des mines de crayon à base de graphite et d’argile, c’était une pointe en métal qui était utilisée, typiquement du plomb (plomb, qui se dit “lead” en anglais, et qui est encore aujourd’hui le terme désignant une mine d’un crayon dans une partie des langues germaniques).
Ces gommes-là agissent donc par une action mécanique en détachant littéralement le tracé du papier. Aussi, elles fonctionnent très bien sur les mines sèches (crayon à papier), mais un peu moins sur les mines grasses, telles que les crayons de couleur : ces dernières finissent par s’étaler grassement sur le papier et à inhiber la formation des copeaux de la gomme, qui finit alors salie. De plus, si l’on a fortement appuyé lors de l’écriture au crayon, la mine se fixe trop profondément dans les aspérités du papier et la gomme ne peut plus la retirer.
Les gommes bleues, abrasives
La confection d’une gomme est un équilibre entre plusieurs paramètres :
- la dureté, pour mieux frotter ;
- la souplesse et l’élasticité, pour ne pas abîmer le papier ;
- adhérence, pour mieux accrocher le graphite se trouvant sur le papier.
Les gommes bleues sont-elles nettement moins souples, et également bien plus abrasives, à cause de l’inclusion de grains de sable (de la pierre ponce) comme sur du papier de verre.
Leur fonctionnement est identique à la partie rose de la gomme, mais ils servent alors à effacer du crayon sur des surfaces plus dures : carton, bois, murs… sur lesquelles on peut appuyer davantage. L’explication disant que cette partie de la gomme sert à effacer le stylo est une semi-légende, entretenue par par les fabricants de gommes elles-mêmes, par le marquage d’une pointe de stylo sur la partie bleue.
Pourtant, n’importe qui ayant essayé a vite remarqué que cela ne fonctionnait pas vraiment. Ceci pour une raison assez simple : l’encre du stylo a tendance à pénétrer profondément dans le papier, pas rester en surface comme le crayon, et donc pour effacer ça, il faut y aller bien plus durement, souvent jusqu’à détruire le papier lui-même, ce qui n’est pas but. Pas de problème cependant sur une surface assez solide (carton, bois, un mur) : ici on peut abraser le support pour retirer le crayon (ou l’encre, mais par abrasion du substrat plus que par retrait du tracé).
Il y a pourtant une méthode pour effacer le stylo ! Enfin… certains stylos. Et c’est avec un troisième type de gomme !
Les gommes FriXion® thermoréactives
FriXion est une marque du fabricant de stylos Pilot. Ce stylo est effaçable avec une gomme. Ici cependant, le principe est totalement différent des gommes pour crayons au graphite.
L’action pour les gommes pour crayons est mécanique, mais celui pour les stylos FriXion est thermochimique : l’encre utilisée dans ces stylos est thermosensible avec un fort phénomène d’hystérésis.
L’encre est visible à température ambiante et lorsqu’on achète le stylo, mais dès qu’on le chauffe autour de +60 °C, il réagit et devient invisible.
L’échauffement pour le rendre invisible (ie : l’effacer) est le rôle de la gomme : frotter la gomme sur l’encre réchauffe localement le papier et l’encre.
L’effet d’hystérésis signifie que l’encre ne réapparaît pas immédiatement en refroidissant à température ambiante. Il est possible de la faire réapparaître, mais il fait refroidir bien en dessous de la température ambiante, à des températures de l’ordre de −10 °C :
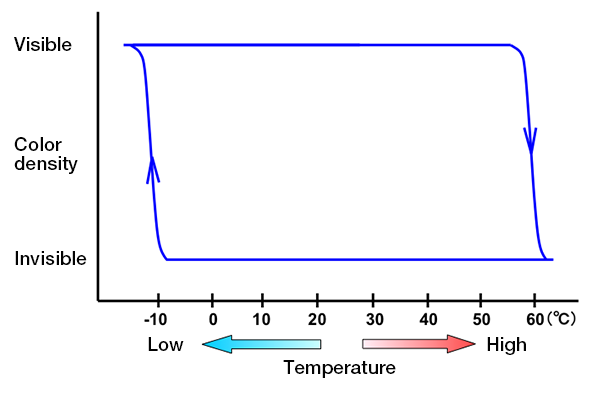
C’est donc différent des encres thermochromiques utilisées dans les tasses thermoréactives ou les bijoux d’humeur : là, l’encre change de couleur lorsqu’elle passe au-dessus d’une température donnée, mais reprend sa couleur initiale si la température repasse en dessous. Les deux transitions se font donc à la même température : il n’y a pas d’hystérésis.
Avec l’hystérésis, l’encre des stylos FriXion® transite d’une phase visible à une phase invisible à +60 °C, et d’une phase invisible à visible à −10 °C. Entre les deux températures, l’encre subsiste dans l’état dans lequel il se trouve, sans bouger. L’hystérésis c’est ça : les deux températures de transitions (dans un sens, puis dans l’autre) ne sont pas identiques.
Ceci signifie aussi deux choses, pour ces stylos :
- un texte écrit avec un stylo FriXion® deviendra invisible sur le papier est chauffé. Par exemple, si le document est laissé dans une voiture au Soleil.
- inversement, un texte effacé avec une gomme peut redevenir visible si on le place au congélateur.
Pour ces raisons, ces stylos ne sont pas recommandés pour des écrits sensibles ou que l’on vise à être pérennes dans le temps.
Si cela est votre besoin, je recommande plutôt les stylos Fisher Space Pen, que l’on peut utiliser sur une plage de température allant de −35 °C et +120 °C et dont l’encre est censée rester inaltérée durant au moins un siècle. Ces stylos sont également remplis de science, notamment pour être capables d’écrire à l’envers et en apesanteur !
Conclusion
Les gommes que l’on trouve dans une trousse d’écolier fonctionnent de différentes façons, en fonction de la gomme en question. La plupart sont faites de caoutchouc naturel (latex), ou synthétique, auxquelles on incorpore des additifs comme du soufre (pour le rendre plus durable, des abrasifs (pour les gommes bleues) ou divers pigments.
Les gommes molles, en caoutchouc, fonctionnent par adhésion : il « colle » au graphite du crayon, simplement accroché sur le papier et le décolle ainsi du papier pour l’effacer.
Les gommes plus dures, notamment les gommes bleues contiennent des particules abrasives, typiquement de la pierre ponce, de la silice (du sable) ou du carbonate de calcium (un abrasif plus doux pour ne pas trop abîmer le papier). Ici l’action mécanique consiste à limer la surface du papier pour en retirer les pigments que l’on a écrits dessus, que ce soit du crayon ou du stylo. Le stylo lui-même n’est pas retiré, comme l’est le crayon, mais c’est toute une partie du papier qui l’est. Ceci abîme inévitablement le papier, et c’est pour ça qu’il n’est prévu à la base que pour les surfaces plus résistantes, comme le bois ou le carton.
Certaines gommes sont là pour des encres spécialement étudiées pour s’effacer, ou du moins s’invisibiliser sous l’action de la chaleur. La chaleur est apportée par l’action de frotter la gomme sur le papier. C’est ce qui se passe pour les stylos FriXion®.
Ici l’action n’est donc plus mécanique, mais thermochimique.
Ressources et liens
- Crayon — Wikipédia ;
- How do erasers work? - McGill University ;
- The Two Types of Erasable Ink and Why One Is Much Cooler Than the Other | Office for Science and Society - McGill University ;
- PILOT FRIXION COLOURS ERASABLE FELT TIP PENS ;
- The Science Behind Frixion Erasable Pens | Nippon.com ;
- How do erasers erase?| HowStuffWorks ;
- Mais à quoi sert vraiment la partie bleue de cette célèbre gomme d’écolier ? — Edition du soir Ouest-France — 28/09/2022 ;
Autres articles sur ce blog
Que se passerait-il si l'on tombe dans un trou noir ?
Couleur science par Anonyme le 06/11/2025 à 05:37:00 - Favoriser (lu/non lu)

Il y a beaucoup de fascination qui entoure les trous noirs cosmologiques, mais aussi beaucoup d’incompréhension.
Un trou noir n’est pas un monstre aspirateur de planètes et d’étoiles qui gobe tout ce qui se passe à proximité. On verra pourquoi dans cet article, mais le sujet principal aujourd’hui sera de répondre à la question : que se passerait-il si l’on tombait dans un trou noir ?
L’essence de la question porte sur l’aspect de la déformation de l’espace-temps associé à la proximité d’un trou noir, et sur la perception de ces déformations par quelqu’un qui tomberait dedans mais aussi par quelqu’un d’autre qui le regarderait tomber.
Populairement, les textes répondant à cette question nous apprennent que le temps se mettrait à s’écouler plus vite pour une personne qui tombe, mais que quelqu’un qui la regarderait, verrait au contraire la personne ralentir.
Si l’on n’est pas trop familier avec l’aspect relatif(viste) de l’espace-temps, ces explications peuvent sembler déroutantes, voire renforcer la confusion régnant autour de ces astres. Si ceci comporte son lot d’exactitudes et d’imprécisions, cela n’explique rien.
Qu’est-ce qui fait qu’un trou noir est un trou noir ?
Pour commencer, rappelons ce qu’est un trou noir et ce qu’il n’est pas. Un trou noir n’est pas un aspirateur à matière. C’est avant tout un astre. Et comme tout astre, il a une masse. Généralement une grande masse (plusieurs masses solaires), mais ce n’est pas obligatoire.
Avoir une masse est suffisant pour attirer les autres objets vers soi au moyen de l’attraction gravitationnelle. Un trou noir n’a pas de mécanisme spécifique à lui pour tout « aspirer » : il se contente de l’attraction gravitationnelle, comme les étoiles et les planètes. On pourrait se placer sur une orbite autour, vivre à « proximité » et même trouver une série de planètes orbitant un trou noir.
La différence qui fait qu’un trou noir est un trou noir ne réside donc pas dans une capacité, une force, particulière. Elle réside plutôt dans sa densité. La densité traduit le fait de mettre une masse donnée dans un volume plus ou moins grand. Plus un objet est dense, plus cette masse occupe un volume petit. Et dans le cas d’un trou noir, une masse importante est réduite à un volume minuscule : on parle de la masse d’une étoile dans le volume d’un petit astéroïde.
Ceci a une importance fondamentale. Pour comprendre cela, prenons un astre quelconque, par exemple la Terre. La force d’attraction entre nous et la Terre est donnée par la relation :
$$F = G \frac{m \cdot M_🜨}{r^2}$$
Où :
- G : est la constante de gravitation universelle
- m : notre masse
- M🜨 : la masse de la Terre
- r : la distance vous séparant du centre de masse de la planète.
Si vous êtes debout sur Terre, alors vos pieds sont plus proches du centre de la Terre que votre tête. Pour notre tête, notre r est plus grand et donc la force plus faible : votre tête est donc moins attirée par la Terre que vos pieds. Bien-sûr, pour une Terre qui a un rayon de 6 400 km, et vous qui ne faites que 1,7 m (donc 0,001 7 km), cette différence est minime, totalement imperceptible.
Comprimons maintenant la Terre dans un volume de la taille d’une bille. Désormais, si l’on est debout sur sa surface, votre taille n’est plus du tout négligeable par rapport à la distance au centre de la bille. La différence d’attraction subie par vos pieds et votre tête est immense ! Cette différence est à l’origine d’une force bien particulière, que l’on appelle la force de marée. C’est la même force qui est responsable des marées au sens populaire, dans la mer et les océans. Si la Terre est comprimée dans une bille, cette force de marée vous donnera l’impression de vous étirer très fortement : vos pieds seront davantage tirés vers le sol que votre tête.
Vous l’aurez compris : la masse joue dans l’attraction d’un astre, mais les dimensions (rayons de l’astre, distance à l’astre) jouent sur le gradient de cette force. Le rayon contribue même bien davantage à cause du r². Si le rayon est minuscule, alors la force d’attraction est gigantesque à la surface.
Un trou noir, comme je l’ai dit, c’est précisément une masse gigantesque dans un volume minuscule. Les trous noirs ont donc un champ gravitationnel énorme à leur voisinage. Or, c’est dans les champs gravitationnels intenses des trous noirs que l’on observe des phénomènes particulièrement intéressants… et étranges !
Conséquences d’une masse très concentrée
Tous les objets peuvent devenir un trou noir : il suffit pour cela de les comprimer dans un volume suffisamment petit. Il faudrait une pression incommensurable pour faire ça, mais les équations nous l’autorisent.
Bien-sûr, si l’on comprime quelque chose, cette chose a tendance à rebondir et à résister. C’est le cas d’un ressort par exemple, mais aussi des atomes et de toute la matière.
Pour la gravité, on a vu que plus on est proche du centre de masse, plus la force d’attraction est forte. Donc, si l’on comprime notre ressort suffisamment, alors sa propre gravité l’empêchera de se détendre. Cet exemple avec un ressort est valable, mais il faut bien comprendre qu’il faudrait le comprimer dans le volume 10 000 milliards de fois plus petit de celui d’un proton, ce qui semble impossible.
Toutefois, si l’on y arrivait, alors la gravitation subie par l’ensemble des atomes du ressort seraient plus importantes que la force de rebond du ressort, et ce dernier resterait là, hyper concentré, sans rebondir.
On dit ici que le ressort subit un effondrement gravitationnel : à ce niveau de densité, la gravitation l’emporte sur toutes les autres forces de l’univers. Et lorsqu’on a un effondrement gravitationnel infini, comme ici, on obtient un trou noir.
Si l’on comprimait la Terre dans une bille de 8,87 mm, alors cela le transformerait en trou noir aussi. Pour une étoile de plusieurs millions de km de diamètre, la taille à atteindre est de quelques dizaines de kilomètres (la taille d’une ville humaine, typiquement).
Les implications sont immédiates pour notre Terre transformée en trou noir. Déjà, à 0,9 mm du centre, se formerait une région de laquelle rien, ni même la lumière, ne pourrait sortir. Cette région n’a pas vraiment de surface, mais elle force ce que l’on appelle « le trou noir » : c’est la région qui est totalement noire (précisément parce que la lumière ne peut en émaner). On appelle cette surface[1] sphérique[2], l’horizon des événements. Il ne s’agit pas d’une surface physique, mais d’une région de l’espace d’où il est impossible de s’échapper une fois qu’on s’aventure dedans. À l’extérieur de cette région, la vitesse de libération est encore inférieure à la vitesse de la lumière, et on peut donc s’en tirer, mais pas de l’intérieur.
Ce que l’on appelle communément « trou noir » correspond donc à cet horizon et tout ce qu’il y à de l’autre côté (« dans » le trou noir, donc).
D’où cela vient ?
Pour pouvoir s’échapper de la pesanteur de n’importe quel astre, et donc se défaire de son attraction, il faut une force supérieure à son accélération de pesanteur : si l’on accélère vers le haut plus vite que la gravité nous accélère vers le bas, eh bien on s’élève. C’est ce que fait une fusée au décollage. La fusée maintient cette poussée durant toute son ascension. Mais on peut aussi communiquer toute cette énergie avec une simple impulsion de départ, comme le ferait une balle de fusil ou un trébuchet (pour lesquels les projectiles ne sont pas autopropulsés).
Il apparaît donc une question : quelle vitesse imprimer à un projectile à la surface d’un astre pour que ce projectile se défasse de l’attraction de l’astre ? Ceci se calcule. Il suffit d’intégrer (au sens mathématique) l’accélération de la pesanteur en surface pour obtenir une vitesse « critique » au-delà de laquelle le projectile ne retombera jamais. On parle de vitesse de libération, vl :
$$v_l = \sqrt{\frac{2 \cdot G \cdot M}{r}}$$
Où :
- G : est la constante de gravitation universelle
- M : la masse de l’astre
- r : la distance au centre de l’astre, typiquement sa surface, sinon une altitude quelconque au-dessus de la surface
Sur Terre la vitesse de libération est de 40 320 km/h (ou 11,2 km/s).
Si l’on imprime cette vitesse à un projectile situé à sa surface, alors sa vitesse lui permettra de s’échapper de l’attraction de la Terre et de ne jamais retomber. Bien sûr, la vitesse du projectile va diminuer avec l’altitude, mais l’accélération de la pesanteur diminue aussi avec l’altitude ! En somme, on peut dire que le projectile s’éloigne plus rapidement de la Terre qu’il ne perd en vitesse. La planète ne pourra donc pas retenir le projectile : il finit par s’échapper totalement de l’emprise gravitationnelle, vers l’infini… et au-delà, dans l’espace.
Pour la Terre, cette vitesse est de 11,2 km/s (à sa surface). Pour Jupiter, on parle de 59,5 km/s ; et pour le Soleil, 617 km/s.
Pour le trou noir, au niveau de son horizon des événements, la vitesse de libération atteint 299 792,458 km/s, c’est-à-dire la vitesse de la lumière.
Trous noirs et effets relativistes
Brèves généralités sur les effets relativistes
Je ne vais pas tout expliquer les implications de la relativité (voyez déjà mon article sur la relativité restreinte par exemple, et en attendant que j’en fasse un pour la relativité générale pour en citer quelques-unes). Résumons seulement cela en quelques phrases.
Ce que la relativité restreinte et générale apportent par rapport à la physique classique, ce sont des modèles mathématiques pour les phénomènes que la physique classique n’explique pas, tout en englobant cette dernière. La mécanique relativiste est donc une extension de la mécanique classique.
Cette extension a été rendue nécessaire après avoir constaté que la mécanique classique (Galiléenne & Newtonienne) ne suffisait pas pour expliquer le monde dans certains cas de figures, notamment les hautes vitesses et les forts champs gravitationnels.
La principale innovation apportée est le caractère non absolu de l’espace et du temps. En effet, si dans la vie courante le temps s’écoule et l’espace défile de façon identique pour tout le monde, partout et tout le temps, en dehors de la vie courante — en dehors du cadre de la mécanique classique — ce n’est plus le cas : le temps s’écoule en réalité différemment, et les longueurs ne sont pas les mêmes selon qui les mesure, quand, où et dans quelles circonstances.
Les principaux facteurs qui font que le temps et l’espace sont ainsi « déformés » selon le référentiel considéré, sont la vitesse de déplacement de ces référentiels les uns par rapport aux autres, et l’intensité du champ gravitationnel dans lequel il se trouve.
À simple titre d’exemple : si l’on se déplace à 87 % de la vitesse de la lumière, notre temps s’écoule deux fois plus lentement que pour une personne qui voit ce référentiel se déplacer. Caricaturalement, de deux personnes dont une part en voyage relativiste à 87 % de la vitesse de la lumière, si celui qui voyage voit passer un an, celui qui reste sur Terre verra passer deux ans (en d’autres termes, celui qui part en le 1ᵉʳ janvier 2025 pendant un an reviendra sur Terre le 1ᵉʳ janvier 2026 pour lui, mais le 1ᵉʳ janvier 2027 pour tout le monde sur Terre. Quand on dit que le temps est « fluide » et relatif à un référentiel, c’est exactement ça.
La relativité générale montre que des phénomènes similaires viennent s’ajouter à ça lorsqu’on prend en compte les effets de la gravitation. Une forte attraction gravitationnelle produit ainsi une déformation de l’espace-temps de telle sorte que le temps s’écoule plus lentement et que la métrique spatiale est, elle, contractée.
Tomber dans un trou noir
Considérons deux personnes, Alice et Bob : Alice va voyager dans un trou noir. Bob va garder ses distances et observer Alice. Le but de l’expérience est de décrire ce que verront Alice et Bob, chacun de leur côté, en gardant en tête que le trou noir modifie — notamment — l’écoulement du temps. On se doute qu’Alice va subir des effets relativistes que Bob ne connaîtra pas.
Ce que vit Alice qui tombe dans le trou noir
Alice tombe dans le trou noir. Elle va subir les effets de la gravitation du trou noir et traverser l’horizon des événements. Son voyage sera donc sans retour.
Bien qu’elle subisse des effets relativistes, elle ne les sentira pas : pour elle, tout se passera normalement : son référentiel reste — de son point de vue — tout à fait ordinaire. Son horloge continuera — pour elle, encore une fois — de fonctionner comme à l’ordinaire : il s’agit d’une chute « normale ». Elle ne verra même pas le moment où elle aura traversé l’horizon des événements.
Vu que le trou noir se trouve devant elle et pas derrière, il y a un gradient dans l’intensité du champ de pesanteur le long de sa trajectoire de chute : ce qu’elle verra donc en revanche, c’est la déformation de l’espace-temps située sur cette trajectoire : devant elle, et derrière elle. Devant Alice, en direction de la singularité, l’espace-temps est davantage déformé. Et derrière elle, il est moins déformé.
L’écoulement du temps, pour commencer : devant elle, le ralentissement est visible et d’autant plus prononcé qu’elle regarde loin. Si une montre était tombée un peu avant elle, Alice verrait cette montre tiquer moins vite, et même de moins en moins vite au fur et à mesure de la chute, jusqu’à s’arrêter une fois à la singularité. Fait remarquable : si le temps lui-même ralentit, la chute semble ralentir aussi, et la montre mettra un temps infini a rejoindre la singularité, du point de vue d’Alice qui suit l’horloge. Toutefois, Alice elle-même, qui reste dans son propre référentiel, avec son temps propre, atteindra bien la singularité en un temps fini (et la montre aussi, mais pas selon Alice).
En ce qui concerne l’espace, donc les longueurs spatiales, celles-ci sont comprimées : la montre pourrait sembler se rapprocher, même si en réalité il n’en est rien, et c’est même l’inverse. Bob, qui regarde tout ça, pourrait se dire qu’Alice se rapproche asymptotiquement de l’horloge. En réalité, Alice ne verra pas cela : d’une part, car son référentiel lui semble normal, mais d’autre part, car tout ce qui lui servirait à mesurer tombe avec elle !
Derrière Alice, c’est-à-dire pour Bob, le temps est moins ralenti. Le référentiel d’Alice voit son temps s’écouler plus lentement, donc c’est comme si le temps de Bob s’accélérait, du point de vue d’Alice. Alice verrait donc Bob évoluer de plus en plus vite : Bob vieillirait à vue d’œil. Ce qui pour Alice ne constitue que quelques minutes, correspond à plusieurs années pour Bob. Ce phénomène s’accélère au fur et à mesure de la chute. Chaque minute correspond peu à peu à une semaine, à un an, puis à 10 ans, puis à un siècle, et ainsi de suite.
Sa chute étant désormais impossible à annuler, elle verrait toute l’histoire future de l’univers qu’elle laisse derrière elle…
Ce que vit Bob qui regarde Alice tomber
Ce qui pour Alice est une chute à une vitesse perçue normalement, correspond pour le reste de l’univers à toute l’éternité qui passe. Bob, s’il était éternel, verrait Alice tomber indéfiniment, et de plus en plus lentement. Il ne pourra toutefois la sauver.
En vrai, Bob finirait par ne plus rien voir : en effet, Bob voit Alice grâce aux rayons de lumière issus d’Alice. Or si Alice traverse l’horizon des événements, la lumière tombe avec elle, sans pouvoir rejoindre Bob. Qui plus est, juste avant l’horizon des événements, le phénomène de redshift ferait que les longueurs d’onde des rayons de lumière d’Alice s’allongent : le domaine visible devient de l’infrarouge, puis des ondes radio, etc. Bob verrait Alice tomber et devenir de moins en moins visible, avant de disparaître dans l’obscurité, comme transparente, invisible.
Inversement, Alice recevrait toujours plus de lumière en provenance de Bob : il s’agit de la lumière émise par tout le futur de Bob.
Ceci est abstraction faite des effets gravitationnels (non forcément relativistes), qui ont en fait quelques effets néfastes supplémentaires sur la santé d’Alice. Les forces de marée, mentionnées plus tôt, sont les principales responsables ici. Si le trou noir est suffisamment massif, les forces de marée ne lui seront perceptibles que bien après qu’elle a franchi l’horizon des événements.
Ses effets feront que la différence d’attraction au niveau de ses pieds (considérant qu’elle tombe les pieds en avant) avec l’attraction au niveau de la tête deviennent très importante. Ces forces seront suffisantes pour disloquer Alice en deux, puis en quatre, puis en plein de morceaux, jusqu’au niveau cellulaire (chaque cellule sera coupée du reste), puis moléculaire, atomique, sub-atomique… Ce qui commence comme Alice sautant dans le trou noir finira comme une longue traînée de particules dirigées vers le centre du trou noir. On appelle ça la spaghettification.
En plus de ça, si le trou noir était déjà orbité par de la matière, alors la matière la plus proche du trou noir tourne si rapidement autour qu’elle s’échauffe jusqu’à émettre des rayons X, juste avant de traverser l’horizon des événements. Ces rayonnements étant létaux à haute dose, cela contribue également à la dégradation de la bonne santé d’Alice.
Conclusion
Ce qu’il faut comprendre avec la relativité, c’est que cette théorie tire son nom du fait que tout est relatif. Par relatif, on entend donc quelque chose qui se compare à autre chose, contrairement à quelque chose d’absolu, qui ne dépend pas d’une comparaison avec quelque chose d’autre.
Dans la vie courante, quelque chose d’absolu serait la couleur d’un objet, mais quelque chose de relatif serait son caractère clair ou foncé : il est plus foncé ou plus clair qu’un autre objet.
En relativité, ce sont les notions de temps (les durées), d’espace (les distance) et les vitesses qui sont relatives entre les référentiels. Deux référentiels, deux personnes si vous voulez, vont vivre des durées et des déplacements qui ne selon pas identiques en fonction de qui les mesure, et dans quel cas de figure, notamment de déplacement, ou d’intensité du champ de pesanteur.
Si je me déplace vers vous, alors la distance que j’ai parcourue sera plus courte pour moi avec ma règle que vous avec la vôtre. Similairement, la durée du trajet sera plus courte selon moi que selon vous. Ce n’est pas une impression, ni une imprécision : le temps s’écoule moins vite pour moi si je la mesure quand je me déplace.
La partie importante, en relativité, est le « pour moi » : tout est une question de point de vue. Tout, à l’exception de la vitesse de la lumière, et des lois physiques : ces deux choses sont les seules à rester absolues. Peu importe qui la mesure, quand, où, et dans quelles conditions : la vitesse de la lumière sera toujours la même.
Le champ de gravitation intervient aussi dans ces distorsions de l’espace et du temps tel que mesuré par les uns et les autres. Les durées vécues et les distances parcourues sont ainsi différentes selon qu’on se trouve dans un fort potentiel gravitationnel, ou un faible.
Ce cas de figure là est notamment présent dans la vicinité d’un trou noir. C’est donc pour cela que si une personne tombe dans le trou noir, le temps s’écoulera et les distances défileront différemment que pour quelqu’un qui est à bonne distance de l’astre massif.
J’insiste sur le fait que chaque personne ne ressentira rien : pour elle, tout sera normal. Ce n’est qu’en comparant notre perception à celle d’autres observateurs que l’on peut dire si notre temps ou notre espace s’écoule plus vite ou plus lentement que celui d’un autre.
Pour un trou noir, la gravitation est très sensiblement d’autant plus forte qu’on en est proche. En matière d’écoulement du temps, ce dernier est de plus en plus lent lorsqu’on s’en approche. Une personne qui tombe dedans aura une horloge ralentie, même si elle ne le ressentira pas elle-même. C’est quelqu’un situé plus loin du trou noir qui verra la personne ralentir jusqu’à l’infini. Inversement, la personne tombante verra cet observateur accélérer, jusqu’à vieillir à vue d’œil, lui et tout l’univers extérieur au trou noir.
Enfin, notons que ceci est ce que nous dit la relativité. La relativité est une théorie née des observations du cosmos. Elle nous prédit également d’autres choses, dont certaines ont à leur tour été confirmées par l’observation. C’est le cas des trous noirs eux-mêmes.
Toutefois, ce qui se passe dans le trou noir lui-même, reste un mystère : la théorie de la relativité ne fonctionne plus très bien à ces échelles : les résultats produits par leurs équations sont aberrants. Les phénomènes décrits dans cet article, concernant Alice et Bob sont basés sur des observations réelles. Les déformations temporelles et spatiales sont observées, néanmoins (mais pas pour des gens que l’on enverrait dans un trou noir, évidemment).
Notes
1. En vérité, il n’y a pas de surface physique solide, sur lequel on pourrait marcher. Il s’agit ici d’une surface au sens mathématique : une forme (ici : fermée et sphérique) avec un intérieur et un extérieur. Il s’agit donc plus d’une limite mathématique qu’une « surface ».
2. Pour un trou noir le plus simple, c’est-à-dire non rotatif et non chargé électriquement.
3. Précisons que si la masse est source d’un potentiel gravitationnel, il en est aussi pour toute forme d’énergie : la masse n’étant qu’une forme d’énergie parmi d’autres.
Pourquoi certains aciers sont-ils aimantables et d’autres non ?
Couleur science par Anonyme le 02/10/2025 à 05:01:00 - Favoriser (lu/non lu)

Le fer et l’acier sont ferromagnétiques : ils sont attirés par un aimant. Certains aciers, notamment une partie des aciers inoxydables par contre, ne le sont pas et cela peut surprendre. Voyons pourquoi, et en détails.
Un inox ?
Le fer et l’acier (non-inox) sont sensibles à l’action de l’oxygène, de l’eau, des acides… Le fer contenu dans l’acier s’oxyde et perd alors toute cohésion avec le reste du métal : l’ensemble s’effrite, expose alors des zones propres, qui vont alors s’oxyder à leur tour, s’effriter et ainsi de suite. Laissé au temps et aux éléments, l’acier normal finit totalement effrité et rouillé, perdant toute intégrité structurelle.
Ce que l’on appelle « inox » est le diminutif de « acier inoxydable ». Il s’agit d’un alliage d’acier — lui-même déjà un alliage de fer et de carbone — dans lequel on a incorporé quelques autres éléments, dont celui qui le rend résistant à l’oxydation : le chrome, à raison d’au moins 10,5 % de chrome, mais pouvant monter jusqu’à 30 %. Le chrome a une affinité plus importante que le fer avec l’oxygène, et il va s’oxyder en premier, en particulier le chrome en surface :
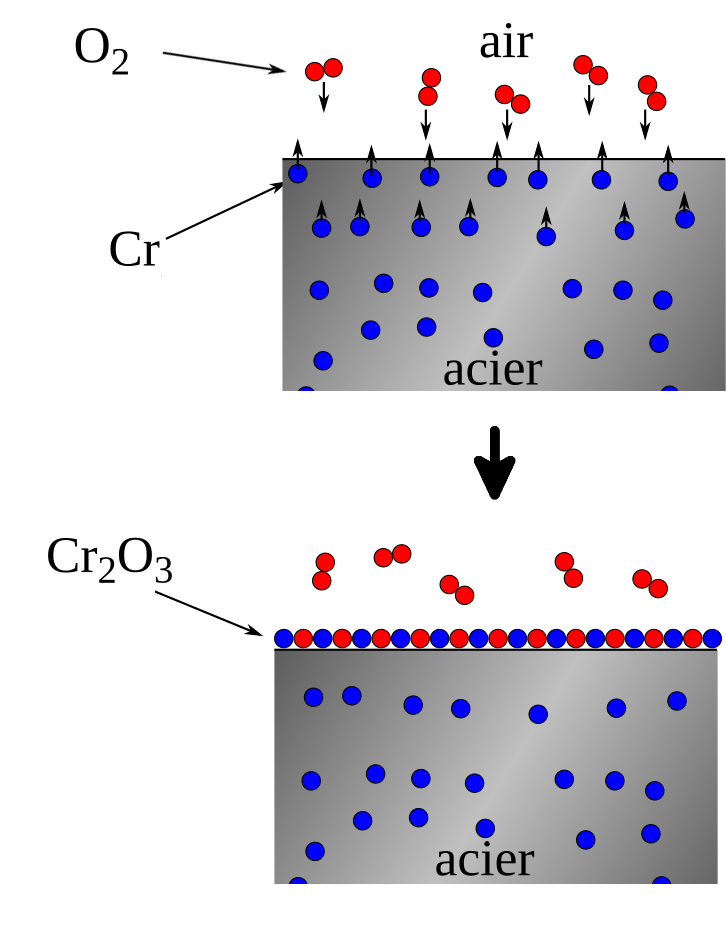
L’acier inox va très rapidement se recouvrir d’une couche d’oxyde de chrome. Contrairement à l’oxyde de fer cependant, l’oxyde de chrome est au contraire très résistant et va ainsi protéger le reste de l’acier, à la fois contre un effritement et contre toute rouille.
D’autres métaux ou alliages font sensiblement la même chose : aluminium, titane, argent, laiton, bronze… Ces métaux sont aussi sensibles à l’oxygène, mais leur surface est rapidement oxydée et protégée par cet oxyde. Ce phénomène, qu’il soit naturel ou provoqué de façon volontaire par un traitement de surface s’appelle la passivation.
L’acier « inox » est un terme générique qui désigne une large gamme d’alliages à base acier et chrome. La plupart du temps, on y ajoute également du nickel (autour de 10 %, mais parfois jusqu’à 35 %) pour le rendre plus solide. Pour la recherche de propriétés mécaniques, chimiques, de biocompatibilités plus fines, on peut y inclure également du titane, du molybdène, du tungstène, du vanadium… en quantité bien plus faible.
Voilà pour la présentation. Maintenant, pourquoi certains inox sont magnétiques et d’autres non ?
Une question de structure cristalline
Au sein d’un matériau sous sa forme solide, les atomes sont le plus souvent organisés en motifs répétables : on parle alors d’un réseau cristallin. Certains matériaux peuvent se présenter sous plusieurs formes différentes, dépendant notamment des conditions présentes à sa formation : température, vitesse de refroidissement, pression, chimie du milieu…
C’est le cas du carbone, pour prendre un exemple bien connu. Si le motif cristallin est hexagonal plat, cela forme un empilement de feuillets appelés graphène et on obtient du graphite, le même que celui des mines de crayons. Si le motif est cubique, on obtient du diamant[1]. On dit que le diamant et le graphite sont deux allotropes du carbone (et il en existe d’autres). On constate déjà que différents allotropes ont des propriétés très différentes.
Le fer présente lui aussi un certain nombre d’allotropes, la plupart dépendant de la température. Ainsi, à température ambiante et jusqu’à 774 °C, le fer est dans sa forme fer-α (« fer alpha »), aussi appelé ferrite, qui est une configuration cristalline de type cubique-centré (body centred cubic, BCC).
Cela correspond à un maillage cristallin en forme de cubes avec un atome supplémentaire au centre du cube.
Entre 910 °C et 1 394 °C, les atomes se réorganisent et forment du fer-γ (« fer gamma »), appelé austénite. Il s’agit ici d’une configuration cubique face centrée (face centered cubic, FCC). La maille de base est toujours cubique, mais ici c’est chaque face du cube qui présente un atome en plus (et rien au centre).
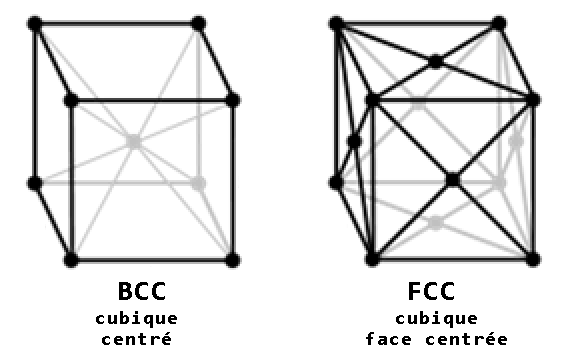
L’une ou l’autre de ces configurations prennent forme à cause de la recherche d’une stabilité du fer, notamment par le changement du moment magnétique de spin (ou simplement « spin ») des électrons non appairés des atomes de fer.
À son tour, le spin va déterminer la proximité des atomes entre eux, et par suite la structure cristalline du matériau dans son ensemble.
Vous l’aurez compris : différents types d’alliages d’aciers inoxydables ont des configurations électroniques différentes, ce qui produit des structures cristallines différentes aussi, et donc également différentes propriétés magnétiques.
À savoir que pour l’acier, la structure BCC est ferromagnétique, et la structure FCC est paramagnétique.
Différences entre le fer-α et le fer-γ
Dans le ferrite (fer-α, ferromagnétique, structure BCC), les électrons non-appairés des différents atomes de fer vont se stabiliser en adoptant des spins identiques.
Lors d’une excitation par un aimant, les moments magnétiques de tous les atomes s’alignent et le matériau est fortement attiré. Cet alignement est même rémanent : il subsiste après le retrait de l’aimant. C’est la raison pour laquelle certains tournevis, ou même une simple aiguille, restent aimantées après les avoir frottées à un aimant.
Dans l’austénite (fer-γ, paramagnétique, structure FCC) les atomes de fer sont plus proches les uns des autres que dans le ferrite. Les orbitales se recouvrent davantage et la stabilité s’atteint ici plutôt par un alignement antiparallèle des spins des électrons non-appairés.
Un champ magnétique extérieur a plus de mal à les orienter « de force », et l’attraction par un aimant est bien plus faible, voire inexistants. De plus, cette aimantation disparaît lorsque l’aimant disparaît
Et dans l’inox ?
L’inox est de l’acier avec un fort pourcentage de chrome et de nickel. Le chrome et le nickel sont, de façon intéressante, également ferromagnétiques, quoique bien moins que le fer. Toutefois, au sein d’un inox, le nickel en particulier pousse l’acier dans sa globalité à former une structure FCC, qui n’est pas ferromagnétique.
Le chrome quant à lui peut, dans certains cas, stabiliser la configuration austénitique de l’acier — qui est FCC — à température ambiante, le rendant non-ferromagnétique ; alors que normalement, l’acier austénitique chaud redevient férritique à température ambiante.
Dans l’ensemble, donc, grâce à la présence du nickel, et selon les traitements en présence du chrome, les alliages d’acier inoxydables peuvent ou non présenter un caractère ferromagnétique, et donc être attiré par un aimant.
Le choix d’un type d’alliage ou d’un traitement dépend des propriétés recherchées. Le magnétisme est alors un effet de bord, à moins que ce soit lui-même la propriété recherchée.
Note : l’acier peut se présenter également sous une autre forme courante appelée martensite : c’est ce que l’on obtient lors de la trempe de l’acier ou lors de certains traitements mécaniques (y compris à froid). Ici, le cristal BCC du fer est fortement perturbé par la présence d’atomes de carbone isolés par un refroidissement brusque, au point de se réorienter la structure cubique centrée en une structure tétraédrique centrée (BCT). C’est la conséquence d’un refroidissement brutal (la trempe), qui empêche la migration du carbone en « îlots ». Cette structure maintient les liaisons cristallines tendues, durcissant fortement le métal obtenu, mais la rendant également plus cassant. La martensite est généralement ferromagnétique aussi.
Conclusion
Si l’on entend parfois que l’inox n’est pas magnétique, ce n’est donc que partiellement vrai. Certains inox ne sont effectivement pas attirés par des aimants, mais d’autres le sont bel et bien. En cause la phase cristalline. Cette phase peut être déterminée par la composition, le traitement thermique ou mécanique subi (certaines étapes de mise en forme par forgeage modifient la structure cristalline).
Si je résume dans un tableau :
| Type d’acier | Phase | Composition | Structure | Aimantable | Exemples |
|---|---|---|---|---|---|
| Ferrite | Fer-α | Fe, ou Fe, C | BCC | Oui | Fer et acier² à température ambiante |
| Austénites (incl. inox) | Fer-γ | Fe, C, Cr, Ni, Mn… | FCC | Non | Acier² entre 910 °C et 1 394 °C ; Inox 304, 316… |
| Martensites | Fer-α | Fe, C, Cr… | BCT | Oui | Aciers² et Inox trempés 410, 420, 440… |
À titre d’expérience à faire chez vous, vous pouvez vous promener dans la maison avec un aimant et tester les différents éléments en acier ou en inox se trouvant chez vous. Attention à ne pas confondre avec de l’aluminium, du nickel, du laiton, ou d’autres métaux.
Parmi les pièces en aciers inox qui ne réagiront pas, j’ai trouvé notamment chez moi :
- certaines poignées de portes ou fenêtres ;
- les parois ou couvercles des casseroles en inox (mais pas le fond, qui contient de la fonte) ;
- la robinetterie en inox.
- …
Notes et références
- [1] : la structure du diamant n’est pas exactement cubique, mais dérive du cubique face centrée avec en plus un atome dans chacune des diagonales ; appelé, justement, structure « cubique diamant ».
- [2] : ici quand je parle d’acier, il s’agit d’aciers simples, alliages de fer et de carbone, sans autre additif comme dans l’inox.
Références :
- Tempering (metallurgy) — Wikipedia ;
- Autenite — Wikipedia ;
- ELI5: Why is some stainless steel magnetic and other stainless steel is not magnetic? : explainlikeimfive ;
- Is stainless steel magnetic? - thyssenkrupp Materials ;
- Easy Inox | Le magnétisme de l’inox : mythes, réalité et applications.
Image d’en-tête de Google AI / Gemini.
C’est quoi les verres auto nettoyants ?
Couleur science par Anonyme le 04/09/2025 à 04:52:00 - Favoriser (lu/non lu)

Le verre est un matériau très ancien, mais la technologie actuelle est capable de lui conférer des propriétés diverses et fascinantes. Il est transparent par nature, mais on peut :
- l’opacifier sur demande, grâce aux UV ou grâce à l’électricité
- le rendre polarisant ;
- le rendre transparent dans un seul sens ;
- le rendre résistant à la température ;
- ou encore hydrophobe.
- et en l’alliant avec du plomb, cela devient du cristal, aux propriétés optiques et acoustiques particulières.
Une des possibilités supplémentaire est de le rendre auto-nettoyant et auto-désinfectant.
Le côté nettoyant repose en réalité sur une action de l’eau. Cette action est altérée d’une façon avantageuse par le revêtement qu’on mettra dessus.
Ce revêtement peut être aussi bien hydrophobe que hydrophile.
Sur une vitre rendue hydrophobe, l’eau perle sans s’accrocher. La saleté accumulée (poussière, bactéries, fientes d’oiseaux…), est alors entrainée par l’eau et évacuée, rendant la vitre propre, alors qu’une vitre normale, bien plus hydrophile, aurait maintenu la goutte d’eau en place et son assèchement aurait fixé la saleté sur la vitre.
Inversement, sur une vitre dont le traitement est hydrophile, et donc où l’eau s’étend dans un fin film uniforme, la saleté est également étendue, mais le revêtement comprend alors des composés comme le dioxyde de titane, qui agit comme un catalyseur dans la décomposition des molécules organiques par les UV. Le côté hydrophile permet d’augmenter la surface de contact avec le verre et son revêtement.
Pour rappel, un catalyseur est un composé qui accélère une réaction chimique sans faire partie de cette réaction. Les UV décomposent naturellement les composés organiques avec le temps, mais c’est beaucoup plus rapide avec un traitement spécifique. Le dioxyde de titane ici n’est donc pas consommé et reste sur la vitre.
Les composés organiques dont il est question peuvent être de la saleté, mais aussi des bactéries. Une vitre qui débarrasse sa surface de ça est donc automatiquement désinfectante. Sur une vitre exposée à la pluie et à la lumière du Soleil, l’ensemble est passif.
En laboratoire, pour la stérilisation, on peut utilise un système à UV, qui est plus pratique qu’utiliser une brosse et divers produits (alcool, chlore, ozone…). Les traitements auto-nettoyants améliorent l’action des UV.
Ces verres spéciaux sont également utilisés sur certaines protections d’écrans de téléphones haut de gamme, mais il faut que l’ensemble laisse toujours fonctionner le côté tactile et reste entièrement transparente.
C’est quoi l’effet tunnel en physique quantique ?
Couleur science par Anonyme le 07/08/2025 à 18:32:00 - Favoriser (lu/non lu)

L’effet tunnel est un exemple d’effet étrange mentionné dès que l’on parle de physique quantique. À quoi correspond-il ? Comment l’expliquer ?
La définition de l’effet tunnel, si je prends Wikipédia, c’est ça :
L’effet tunnel désigne la propriété que possède un objet quantique de franchir une barrière de potentiel même si son énergie est inférieure à l’énergie minimale requise pour franchir cette barrière.
Ça semble très compliqué, et cet article va essayer de clarifier tout ça.
Dans cette définition, ce qu’ils appellent « un objet quantique » est typiquement une particule élémentaire, par exemple un électron. Dans la suite de l’article, l’on prendra effectivement un électron en exemple, mais le principe reste similaire pour toute autre particule.
Modèle atomique
On dépeint classiquement un atome comme des électrons sur des orbites fixes autour d’un noyau central. Cette vision est populaire, mais loin de la description moderne de l’atome. Comme expliqué dans mon article sur le modèle atomique et les couches électroniques, on sait aujourd’hui que les orbites des électrons ne sont pas comme ça. En fait, même les électrons ne sont pas comme ça : on ne les voit plus comme des petites billes.
Dans la compréhension moderne du modèle atomique, les électrons sont représentés par une fonction d’onde ayant une composante probabiliste. Cela veut dire que l’électron correspond à tout le nuage à la fois. Le nuage contient l’électron et ce dernier ne prend une position fixe que lorsqu’on le mesure. Cette position enfin, est, elle, définie par des probabilités.
L’on connait très bien les probabilités, mais pas l’issue de ces probabilités. Voyez ça comme un jeté de dés : on sait que l’on a très exactement une chance sur six de faire un 6, mais on ne sait pas prévoir si le prochain lancé sera effectivement un 6.
Cette nuance est très importante et elle a deux conséquences :
- La première c’est que ce n’est pas parce que l’on a à faire à des probabilités que l’on nage dans le flou. On connait les probabilités.
- Inversement, la parfaite connaissance de règles de probabilité ne nous donne pas une vue sur l’avenir pour autant. Les probabilités sont connues, pas leur issue.
Poursuivons. Un nuage — météorologique je veux dire — n’est pas clairement délimité. De loin, on voit une zone aux allures finies, mais quand on s’en approche, on entre dedans de façon très progressive, comme dans un brouillard. Si l’on voulait délimiter ce nuage, il faudrait poser une règle arbitraire. Par exemple « le moment où l’air contient 25 gouttelettes par mètre cube, pas avant », ou encore « le moment où 5 % de la vision est obstruée par des gouttelettes ».
En physique quantique, c’est un peu pareil. Le nuage électronique autour d’un atome s’étend théoriquement jusqu’à l’infini, et englobe donc tout l’univers. Pour que l’on puisse avoir une représentation plus compréhensible, on va délimiter la zone qui a une probabilité de 90 % de trouver l’électron. Dans ce cas, l’électron a 90 % de chance de se trouver dans cette limite et seulement 10 % ailleurs ; où « ailleurs » est synonyme de « partout ailleurs dans l’univers » :

Cette probabilité peut être représentée par une fonction : la fonction de distribution de présence de l’électron. En particulier, la fonction de distribution radiale donne la probabilité de présence en fonction de la distance au noyau, le tout dans une direction donnée — les nuages électroniques n’étant pas forcément isotropes, on aura aussi une composante directionnelle, ou angulaire, autour du noyau, mais on va ignorer ça pour le moment (et de toute façon elles n’ont pas d’importance pour les électrons 1s ou 2s).
La représentation graphique en 2D de la fonction de distribution radiale donne une courbe, où l’origine représente le centre du noyau, x la distance à ce noyau et y la probabilité de trouver l’électron.
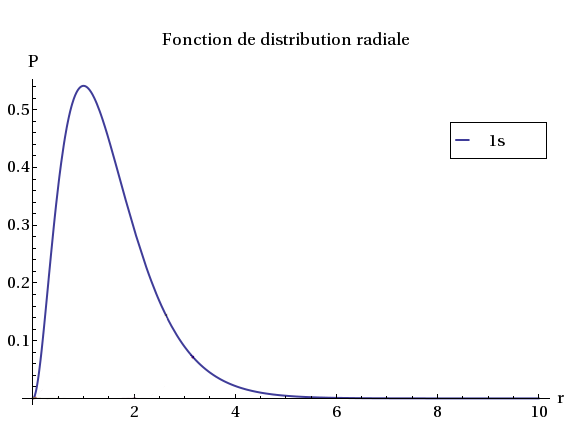
Pour l’orbitale 1s de l’hydrogène ci-dessus, il y a un seul lobe qui est une sphère centrée sur le noyau. La probabilité est nulle au niveau du centre du noyau lui-même, élevée au niveau du rayon atomique (r=1), mais décroît ensuite très vite vers zéro si l’on s’en éloigne.
La probabilité de trouver l’électron 1s loin du noyau est donc très faible. Faible, mais pas nulle.
Notion de barrière de potentiel
Une barrière de potentiel, classiquement, c’est une colline vers laquelle l’on fait rouler un ballon. Si le ballon ne va pas assez vite, alors elle ne franchira pas la colline. Le potentiel gravitationnel est trop élevé pour que le ballon, qui n’a pas suffisamment d’énergie, puisse le vaincre.
En soi, un potentiel peut être de n’importe quelle nature : potentiel électrique, chimique, magnétique, gravitationnel… Si l’on fait rouler un aimant vers un champ magnétique, il peut être repoussé également, faute de rouler assez vite.
Pour l’électron d’un atome donné, la barrière de potentiel peut-être un champ électrique porté par un autre atome. Toutefois, contrairement au ballon qui est totalement stoppé par la colline et ne passera donc jamais la barrière s’il n’a pas assez de vitesse, l’électron n’est pas totalement stoppé lorsqu’il rencontre le second atome : sa probabilité de présence dans l’autre atome est simplement atténuée.
Ainsi, au lieu d’une fonction de distribution comme celle plus haut qui serait tronquée à cause de la barrière, on peut avoir une courbe où la barrière ne fait qu’atténuer la fonction, sans la bloquer complètement :
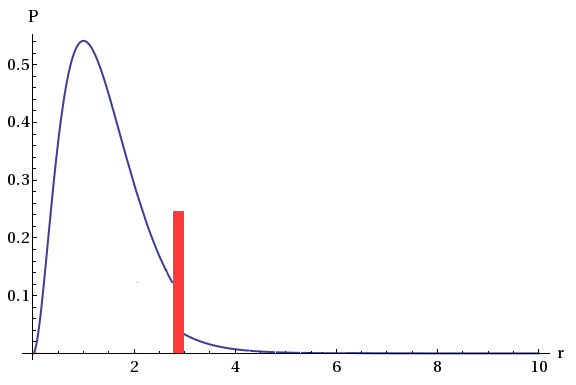
(cette représentation est faite habituellement avec la fonction d’onde directement, pas avec la fonction de distribution, mais les deux sont liées et cette représentation me semble plus simple à comprendre)
Ce qu’il faut voir ici, c’est que si l’on mesure la position de l’électron, alors elle sera de l’autre côté de la barrière seulement 1 % du temps, alors que sans la barrière on aurait pu avoir 10 %. La probabilité d’avoir l’électron de l’autre côté de la barrière est clairement diminuée, mais pas annulée, elle peut s’y trouver, quand bien même cette barrière était initialement trop élevée par rapport à l’énergie de l’électron.
Maintenant, l’on peut imaginer de l’autre côté un atome qui va « emprisonner » notre électron à l’instant même où il aura franchi la barrière. Il suffira donc juste que l’électron se présente de l’autre côté pour l’y piéger. Piéger l’électron revient à modifier sa probabilité de présence afin que désormais, elle soit 99 % à droite et seulement 1 % à gauche. En somme : on l’empêche de retourner d’où elle vient.
Ce piège peut être réalisé par la présence d’un autre atome en manque d’électron (un ion, un cation). D’un point de vue classique : l’électron est alors comme capté par ce cation après s’être échappé de son atome initial. Dans ce cas, on parle d’un puits de potentiel. Classiquement, c’est comme si le ballon tombait dans un trou et y restait.
Si l’on fait le bilan : on a donc un électron qui est passé de l’autre côté d’une barrière alors qu’il n’avait pas l’énergie pour ça initialement. Aucun effet classique ne peut l’expliquer : seule la physique quantique le peut. Cet effet est réel, et c’est cela que l’on appelle l’effet tunnel.
La dénomination provient du fait que si l’on appliquait ça à un ballon, le ballon devrait creuser un tunnel à travers la barrière, à défaut de passer par-dessus.
Comment c’est possible ?
Nous n’avons pas d’yeux suffisamment petits pour aller voir directement le mécanisme responsable de l’effet tunnel. Cela n’empêche pas de voir l’effet ou ses conséquences se produire.
La seule façon de se représenter ça, c’est mathématiquement, avec des équations. L’expérience est alors là pour comparer la réalité à nos prédictions mathématiques, et une concordance permet alors de dire si notre modèle théorique fonctionne ou non. Et la physique quantique, pour le moment, fonctionne incroyablement bien. Les sciences physiques c’est ça : retrouver par l’expérience, par des essais successifs, le modèle mathématique qui décrit le mieux un phénomène rencontré, puis de valider cette équation.
Une équation ne donne pas la raison de l’existence du phénomène, mais elle nous dit si le phénomène s’applique, et si oui, dans quelle mesure. La raison de son existence est une autre question à laquelle répondre est parfois plus délicate.
Pour dire pourquoi et comment ça marche, toutefois, il faut voir que l’électron, son paquet d’onde en fait — l’objet qui combine la particule et l’onde — va interagir avec la barrière de potentiel (ou l’objet qui lui donne source).
Cette interaction est telle que plus le paquet d’onde pénètre dans la barrière, plus elle est atténuée. Et plus il s’atténue, plus il sera enclin à plutôt rebondir contre la barrière :
Si la barrière de potentiel est fine, alors elle n’est pas totalement atténuée lorsqu’elle atteint l’autre côté de la barrière : elle peut donc en ressortir avec une probabilité décente et observable.
Dans la vie courante, on peut observer un phénomène analogue à une impulsion sonore. Quand un son rencontre un obstacle, il y a toujours une partie de l’onde qui est réfléchie, et une partie qui est transmise dans l’obstacle. Si l’obstacle est épais, l’onde transmise finira dissipée et ne sera pas audible de l’autre côté. Si l’obstacle est très fin, la partie transmise franchira l’obstacle en passant à travers.
Ainsi, si l’on est dans une cathédrale, les murs en pierre épais vont favoriser une réflexion des ondes sonores : c’est ce qui donne cet effet de résonance et d’écho. Si l’on recouvrait tous les murs de mousse isolante, l’écho disparaît : l’onde est absorbée et dissipée en chaleur, plutôt que réfléchi ou transmise. Et si l’on remplaçait les murs par des fines cloisons en papier, l’onde sonore va mettre en vibration le papier et quelqu’un de l’autre côté vous entendra facilement : l’onde est transmise sans être ni absorbée ni réfléchie.
Pour un paquet d’onde, on veut le voir de façon similaire : le paquet d’onde va en partie rebondir sur la barrière de potentiel, et en partie pénétrer à l’intérieur, voire, si la barrière est fine, passer à travers.
En n’oubliant pas — et c’est là où l’analogie avec l’onde sonore s’arrête — que le paquet d’onde ne passe pas partiellement à travers : elle n’est pas divisée en deux. C’est sa probabilité qui l’est. Mais l’électron lui-même n’est pas sécable et sa présence ne se mesure toujours qu’à un endroit : on pourra observer la particule aussi bien dans l’un que dans l’autre, par exemple en répétant l’expérience plusieurs fois de suite avec plusieurs électrons : une partie des électrons seront réfléchis par la barrière de potentiel, et une autre partie auront réussi à traverser la barrière de potentiel.
Où observer ce phénomène ?
On voit les conséquences de l’effet tunnel tous les jours et on sait même le mettre à profit.
Dans la nature, un exemple notoire est qu’il fait briller le Soleil. L’énergie nucléaire des étoiles provient de la fusion des protons. Les protons fusionnent quand leur énergie cinétique leur permet de dépasser leur répulsion électrique. Cette répulsion constitue une barrière, appelée barrière Coulombienne, et qui est un type de barrière de potentiel.
Au cœur du Soleil et de beaucoup d’étoiles, la température est trop faible pour que la seule énergie cinétique des protons permette aux particules de franchir la barrière coulombienne. Il faudrait en effet des températures de l’ordre de 100 millions de kelvins, mais le Soleil n’est toujours qu’à 15 millions de kelvins.
Pourtant, la fusion se produit bien. Une explication réside avec l’effet tunnel : on explique le franchissement de la barrière coulombienne par l’effet tunnel. Une fois de l’autre côté de la barrière, les deux protons sont maintenus ensemble par l’interaction forte, qui constitue un puits de potentiel. La température thermodynamique rapproche les protons, mais l’effet tunnel est nécessaire pour ce dernier coup de pouce permettant d’obtenir la fusion.
Quant à l’exploitation artificielle de l’effet tunnel dans notre technologie, on peut citer : la mémoire flash des clés USB, cartes SD, mémoires de téléphones, disques SSD. Ils fonctionnent en piégeant des électrons sur des conducteurs isolés électriquement (les grilles flottantes — ou floating gate). L’isolant est franchi par effet tunnel, et les charges électriques ainsi chargées ou déchargées sur des pastilles isolantes constituent alors les bits stockés dans la mémoire.
Une autre application bien connue est le microscope à effet tunnel : on mesure un courant d’électron plus ou moins fort (permettant de faire des pixels plus ou moins lumineux d’une image globale), et ces électrons passent de l’échantillon au détecteur par effet tunnel.
Ressources
Comment fonctionnent les recharges dessicants pour déshumidificateur ?
Couleur science par Anonyme le 03/07/2025 à 04:47:00 - Favoriser (lu/non lu)

Si les billes dessicants en silicates adsorbent l’humidité de l’air en piégeant les molécules d’eau sur sa surface, les sachets-recharges pour déshumidificateur absorbent l’humidité sur le plan chimique, donc avec un mécanisme différent.
Absorption ou adsorption ?
Pour les billes en silicates, je parle d’adsorption, avec un « d ». À l’inverse, pour les recharges en poudre, je parle d’absorption, avec un « b ».
La différence est fondamentale : l’adsorption concerne un phénomène de surface, alors que l’absorption est un phénomène volumique. Dans le cas des billes en gel de silicates, l’eau est piégée dans les pores nanoscopiques à la surface de la matière. L’efficacité réside dans sa très grande surface spécifique. L’eau ne réagit pas chimiquement avec les silicates, mais est juste coincée dans les pores.
Les dessicants en recharge fonctionnent par absorption. Ils contiennent une poudre blanche de chlorure de calcium anhydre CaCl2. L’humidité vient réagir avec la poudre dans tout le volume : les molécules d’eau se lient aux ions du solide ionique. Notez que ce mécanisme n’est qu’un exemple d’absorption : l’absorption désigne seulement un processus ayant lieu en volume plutôt qu’en surface, pas si ce phénomène est physique, chimique ou d’une autre nature.
Que le pouvoir dessiccateur d’un composé soit obtenu par absorption ou adsorption, dans les deux cas, on parle d’un composé hygroscopique, c’est-à-dire un composé qui a une forte affinité avec l’eau, jusqu’à la retirer de l’air ambiante.
Absorption pour le chlorure de calcium
Le chlorure de calcium, CaCl2, est un solide cristallin ionique : la molécule est polarisée, car les électrons du calcium sont délocalisés vers les atomes chlore.
En présence d’humidité, les molécules d’eau, également polarisées, vont venir se fixer autour des atomes de chlore et de calcium, et y rester. L’eau va présenter son côté positif aux atomes de chlore et son côté négatif aux atomes de calcium et rester ainsi en place par des liaisons ion-dipôles.
Dans cet état, le chlorure de calcium est dit « hydraté » et n’est plus totalement le même composé chimique non plus. Dans son état le plus hydraté, chaque molécule de chlorure de calcium CaCl2 peut retenir typiquement 2, 4 ou 6 molécules d’eau. Par exemple, pour une tétrahydration (donc 4 molécules d’eau), on note cela ainsi :

Dans les pochettes dessiccatrices, la poudre de chlorure de calcium anhydre se charge et se décharge en eau en fonction de l’humidité relative du milieu : le composé « travaille ». Les grains de la poudre se soudent aussi petit à petit entre eux, formant un agglomérat plus ou moins uniforme et solide avec le temps.
Quand le sachet est dur comme et forme un seul bloc ressemblant à du plâtre, on peut se dire que le sachet est à changer.
D’autres exemples de composés hygroscopiques
Outre le chlorure de calcium, la soude caustique (hydroxyde de sodium) ou le bicarbonate de soude (bicarbonate de sodium) sont également de bons absorbeurs d’humidité : laissés à l’air libre, l’eau peut même se liquéfier autour : le composé se dissout dans l’humidité qu’il absorbe !
Le chlorure de sodium, c’est-à-dire le sel de table, est également concerné. Du sel laissé à l’air libre peut devenir collante voire faire comme la soude caustique et se dissoudre dans l’eau qu’elle absorbe. Le sel pourra être placé au soleil ensuite pour le sécher.
Dans certains cas, le composé anhydre et le composé hydraté ont des propriétés physico-chimiques différentes. Ils peuvent par exemple changer de couleur. Un cas bien connu est le sulfate de cuivre : blanc, il prend une couleur bleue vive en présence d’eau ou d’humidité. Il s’agit de l’eau qui libère les ions de leur structure cristalline solide, et ce sont ces ions, libres, qui sont colorés.
De la même manière, l’hydratation du chlorure de cobalt le fait passer du bleu pâle au rouge vif.
Enfin, si un système pour déshumidifier l’air est parfois nécessaire, un système à base de recharges n’est pas forcément pratique. Les pochettes de chlorure de calcium sont plutôt réservées à des petits endroits confinés, avec un très faible renouvellement d’air. J’ai découvert ça dans les phares de voitures à LED : les phares LED ne chauffent pas et ne permettent pas de dégager l’humidité aussi bien que des phares classiques. Les phares modernes sont également hermétiques pour une question de sensibilité à l’eau et à la poussière. Cela nécessite en contrepartie la présence d’un dessicant, qu’il faut périodique remplacer.
Dans les autres cas, notamment pour déshumidifier une pièce de la maison, on préférera des méthodes par condensations : un climatiseur ou un module Peltier refroidit l’air, ce l’assèche par condensation de son eau, qui goute alors dans un réservoir. C’est le principe de fonctionnement de la plupart des déshumidificateurs électriques domestiques. Il n’y a pas besoin de recharges, juste de vider l’eau quand le récipient est plein.
Liens
Comment fonctionnent les thermomètres mini-maxi ?
Couleur science par Anonyme le 05/06/2025 à 04:06:00 - Favoriser (lu/non lu)

Dans un thermomètre de type thermomètre à mercure, on a un tube contenant du mercure, un métal liquide1. Lorsque la température s’élève, le mercure prend du volume et monte dans le tube. La hauteur du mercure est directement liée à la température et il suffit de graduer le tube pour lire la température.
Généralement, les tubes sont terminés en bas par une petite fiole contenant du mercure. Le volume total de mercure étant plus important avec la fiole, la quantité de mercure qui se dilate est plus importante et cela amplifie l’amplitude de la variation de la hauteur de la colonne dans le tube, rendant la lecture plus facile :

Parfois la fiole est masquée dans la coque, qui sert alors aussi de protection.
Dans les thermomètres mini-maxi, l’on se retrouve avec deux colonnes. L’une d’elles est dans le sens du thermomètre normal décrit ci-dessus, mais l’autre, celle du mini, est inversée : les températures froides sont en haut et chaudes sont en bas. Aussi, si la température refroidit, le mercure remonte dans le tube mini.
On a également dans chaque tube une petite pastille qui flotte (littéralement) sur le mercure : ce sont les index montrant les minis et les maxi atteints.

Lorsque le mercure monte ou descend, les index suivent le mouvement, à ceci près que les index ne peuvent toujours que remonter dans le tube, pas descendre. Dans le tube maxi, le haut signifie la température chaude, et dans le tube mini, le haut signifie la température froide. Les index « mémorisent » donc les extrema de température ; d’où le nom d’un thermomètre mini-maxi.
Enfin, le thermomètre dispose d’un bouton de remise à zéro : enfoncé, les deux index redescendent au contact du mercure, remettant à zéro les lectures mini et maxi.
L’ensemble fonctionne sans pile ni source d’énergie extérieure.
Plusieurs questions se posent :
- comment, dans le tube mini, le mercure peut-il remonter avec un refroidissement ? Il devrait remonter (se dilater) avec la chaleur, pas le froid !
- comment fonctionne le bouton de remise à zéro ?
Ce dispositif très commun contient un peu de science très simple, mais le système reste ingénieux.
Si vous avez lu mon article sur le thermomètre de Galilée, avec les capsules colorées, vous savez que ce n’est pas la densité des capsules qui varie, mais la densité du liquide partout autour qui change avec la température. La leçon à en tirer est que la science se cache dans la partie que l’on a tendance à ignorer : le liquide transparent.
Dans le thermomètre mini-maxi c’est pareil : l’on voit le mercure bouger, mais ce n’est pas sa dilatation qui en est la cause, ni celle qui est intéressante. Sa dilatation est imperceptible ici.
De plus, il n’y a pas deux colonnes comme on pourrait croire, mais une seule. Le bouton de remise à zéro cache aussi des choses !
Voyons tout ça.
Un tube de mercure en « U »
Une des astuces utilisées est la forme du tube du thermomètre : il n’y en a qu’un et en forme de « U ». Les tubes mini et maxi correspondent aux deux barres verticales du U.
Le mercure, lui, ne se trouve que dans le creux du U. Le reste est rempli d’alcool transparent et donc invisible.
Dans ce tube en U, la fiole se trouve non pas en bas, mais en haut de la barre du mini et est pleine d’alcool. Le liquide se dilatant n’est donc pas le mercure, mais l’alcool !

La fiole se trouvant en haut, lors de la dilatation2 l’alcool progresse vers le bas au lieu de monter comme dans un thermomètre classique. L’alcool pousse alors le mercure à se déplacer dans le creux du U, et du mini vers le maxi.
Lorsque la température augmente, le mercure descend le tube mini, poussé par l’alcool, et mécaniquement, il remonte du côté « maxi ».
Au final, donc, le mercure ne se dilate pas (ou trop peu), mais est simplement poussé par l’alcool, qui lui se dilate. Inversement, quand la température baisse, il remonte du côté mini et descend du côté maxi, aspiré par la contraction de l’alcool, et suivant donc bien les graduations inversées.
L’ensemble n’est donc qu’un seul et même thermomètre où seul l’alcool se dilate significativement et où le mercure ne constitue qu’une « bouée » qui suit les variations de volume de l’alcool. La forme en U permet de mettre en haut les deux extrémités du volume de mercure, et sur lesquelles l’on a posé les deux pastilles.
Notez que l’alcool est assez fluide pour passer autour des index, qui ne bougent que poussés par le mercure.
Le mercure a une tension de surface assez important pour ne pas mouiller l’index, mais le repousser. Capacité que n’a pas l’alcool.
Et le bouton de remise à zéro ?
Le mercure pousse les index lorsqu’il les atteint, mais les index ne redescendent pas lorsque le mercure se retire. Pour les faire redescendre, on appuie sur le bouton : là, et seulement là, les index redescendent.
Comment ça marche ?
Le bouton repose sur un cadre contenant deux bandes aimantées qui longent les deux tubes. Les index contiennent quant à eux du fer métallique.
Les bandes magnétiques attirent donc les index vers eux, et les plaque contre la paroi du tube.
Le mercure pousse tout juste assez fort pour vaincre le frottement de l’index contre le tube en verre et les faire remonter. Par contre, lorsque le mercure se retire, le poids de l’index lui-même n’est pas suffisant pour le faire redescendre par gravité, et il reste donc plaqué contre la paroi, là où le mercure l’a posé :

Lorsque l’on appuie sur le bouton de remise à zéro, l’on éloigne simplement les aimants des deux tubes. Les index ne sont plus plaqués contre leur tube, et redescendent par gravité… jusqu’à revenir au contact du mercure.
Simplissime, mais il fallait y penser !
Conclusions
À nouveau — et à nouveau pour un thermomètre — la science a lieu ailleurs que là où l’on l’aurait attendu, à savoir dans le liquide (que l’on ne voit pas) entourant le mercure, et non au niveau du mercure lui-même.
Aussi, le bouton de remise à zéro fonctionne, avec des aimants (quoi d’autre ?).
Il s’agit globalement d’une mécanique assez triviale, mais je suis demandé comment ça fonctionnait lorsque je me suis retrouvé avec un tel thermomètre dans les mains.
Maintenant trivial ne signifie pas qu’il n’y a pas de technique derrière : il faut tout de même jauger divers paramètres comme la force des aimants et la quantité de fer dans les index : en contact, l’aimant doit bloquer la descente de l’index sans toutefois bloquer la montée, et quand on appuie sur le bouton, l’aimant ne s’éloigne que de quelques millimètres des deux tubes, mais cela doit être suffisant pour en réduire l’attraction.
Un tel thermomètre peut-être trouvé dans n’importe quel magasin de bricolage pour une quinzaine d’euros. On les trouve naturellement aussi sur Amazon.
Notes
[1] Aujourd’hui, le mercure n’est plus employé en raison de sa toxicité élevée. On préfère utiliser un liquide de type alcool coloré (en bleu ou en rouge typiquement). Pour les thermomètres qui ne descendent pas plus bas que −19 °C (comme les thermomètres médicaux, qui vont généralement de +35 °C à +43 °C) on utilise aussi du galinstan, un alliage métallique liquide de gallium, d’indium et d’étain.
Pour les thermomètres mini-maxi, on a toujours besoin de deux liquides non-miscibles et de densité différentes.
[2] La fiole étant en haut, l’alcool se dilate vers le bas. Lorsque la température baisse, la contraction le fait remonter. Précisons qu’à ces échelles, les forces de cohésion liquide (tension de surface) et de capillarité l’emportent très sensiblement sur les forces de gravité : c’est pour cela que le liquide n’a aucun mal à remonter.
Image d’en-tête : travail personnel.
Comment fonctionnent les encres qui changent à couleur changeante des billets euro ?
Couleur science par Anonyme le 01/05/2025 à 07:26:00 - Favoriser (lu/non lu)

Une technique anti-contrefaçons utilisée notamment sur les billets de banque sont les encres à couleur changeante. On le voit sur les billets de 50 € ou plus, notamment.
Comment ça marche ? Comment une encre peut-être être de plusieurs couleurs ?
Une couleur, zéro pigments
Habituellement, les couleurs sont produites par des pigments. Un pigment est une molécule qui lorsqu’elle reçoit la lumière incidente, absorbe une partie du spectre reçu, et renvoie le reste. La couleur du pigment correspond alors à la partie de la lumière qui est renvoyée.
L’espèce chimique utilisée dans le pigment détermine sa couleur. Si l’espèce chimique (la molécule) ne change pas, alors cette couleur ne change pas
Dans certains cas, les couleurs peuvent être produites sans pigments. C’est le cas de couleurs dites structurelles, où c’est la structure de la matière, l’agencement des atomes au niveau microscopique ou macroscopique qui est responsable de la production des couleurs, principalement grâce à des phénomènes d’interférences ondulatoire de la lumière, mais aussi de phénomènes relativistes, pour la couleur de l’or ou du cuivre par exemple.
Les encres qui changent de couleurs, ou encres optiquement variables tombent dans la catégorie des matériaux qui produisent de la couleur structurelle par phénomène d’interférences. Elles rejoignent donc les bulles de savon, les plumes de paon, les cristaux des pierres d’humeur sur les bijoux, les couleurs sur une flaque d’eau contenant du gazole, les couleurs obtenues avec un CD que l’on éclaire… bref, on en voit partout bien qu’on ne se pose pas souvent la question.
Contrôler la structure permet de choisir la couleur finale que l’on verra, mais on pourra aussi obtenir un effet de changement de couleur en fonction de l’inclinaison de la surface. Dans le cas des billets de 50 € mentionné au début, la partie encrée varie du vert au violet.
Origine d’une couleur structurelle
La couleur structurelle découle généralement de phénomènes d’interférences. On les reconnaît à leur aspect métallique, ou irisés.
Au cours de ces phénomènes, un rayon de lumière incidente issu de la lumière ambiante se retrouve scindé en deux rayons identiques (même direction, même longueur d’onde) mais décalés, déphasés. Quand ces deux rayons se recombinent, ils agissent l’un sur l’autre : ils interfèrent. Leur amplitude peuvent alors s’additionner ou se soustraire en fonction du déphasage :

Si l’on a deux couleurs — deux longueurs d’ondes différentes — il est possible que l’une soit totalement annulée, et l’autre soit au contraire augmentée. Le déphasage est bien identique pour les deux longueurs d’onde, mais chaque longueur d’onde ne va pas réagir de la même façon.
C’est ce mécanisme qui permet de colorer des surfaces structurellement à partir d’une lumière blanche polychromatique.
Origine des interférences
Pour obtenir une couleur structurelle, il faut que les rayons incidents soient scindés. Les rayons ainsi obtenus vont interférer et produire la couleur par addition ou soustraction.
L’origine de la scission se produit typiquement avec des revêtements présentant une couche mince transparente, des petits orifices, ou rainures très fines.
Quelques exemples peuvent être :
- les sillons d’un CD-Rom (réseau de diffraction ; rainures)
- l’épaisseur d’eau d’une bulle de savon (couche mince)
- une couche d’huile ou de gazole sur une flaque d’eau (couche mince)
- les plumes de paon, de coq, de canard Col Vert, de pigeon (réseau de diffraction)
- les écailles de poisson, le dos de certains scarabées, les ailes de certains papillons (réseaux de diffraction + couche mince)
Dans ce cas des interférences par couche mince, une partie de la lumière est directement réfléchie sans entrer dans la couche transparente et l’autre passe dans la matière, se réfléchit à l’intérieur puis en ressort :

On peut remarquer que la partie transmise dans la couche mince du rayon va effectuer un trajet supplémentaire par rapport à la partie du rayon qui est réfléchi en surface. On parle d’une différence de marche dans le trajet optique.
C’est précisément la valeur de cette différence de marche qui va constituer le déphasage : les deux ondes initialement en phase au moment de se scinder en deux, vont être décalées au moment d’interférer.
Évidemment, le déphasage va dépendre de l’épaisseur de la couche mince, ainsi que de sa nature, mais ce n’est pas tout. L’inclinaison des rayons incidents va également être importante. En effet, plus le rayon est incliné, plus le trajet optique dans la couche mince va être importante, et cette augmentation fera varier le déphasage :

Sur la figure ci-dessus, on voit très bien que la différence de marche dépend de l’inclinaison. Il en résulte que selon l’inclinaison des rayons incidents, les couleurs issues des interférences vont également varier.
Cas des encres optiquement variables
L’effet où l’encre change de couleur en fonction de l’inclinaison vient de là : quand on incline le papier encré, on modifie en direct l’incidence et donc le déphasage, et par suite, la couleur résultante varie également.
Le déphasage est le même pour toutes les longueurs d’ondes, mais si l’on prend l’exemple d’un déphasage de 200 nm, celui-ci va totalement annuler les longueurs d’ondes de 400 nm (bleues), mais seulement partiellement les longueurs d’ondes de 500 nm (vert), 600 nm (jaune), ou rouges. Dans ces conditions, le bleu est annulé et retiré du spectre : la lumière blanche sans le bleu devient alors orange.
Si cette fois le déphasage est de 300 nm, les longueurs d’ondes de 400 nm (bleues) ne sont plus totalement annulées, mais le 600 nm (jaune), si. Le spectre blanc est donc dénué de jaune, et sera principalement rouge-bleu, donc violacé.
Selon l’angle, donc, les couleurs qui ressortent après interférences varient, et c’est ce qui provoque ces changements :

Conclusion
Les encres qui changent de couleur en fonction de l’orientation fonctionnent par des interférences ondulatoires lumineuses : la lumière interfère, soit constructivement, soit destructivement. Il en résulte que l’encre soit atténue, soit accentue certaines couleurs. De la lumière blanche, on passe donc, par exemple, à de la lumière verte. Et vu le fonctionnement de ces interférences, c’est l’angle d’incidence qui détermine quelle couleur est détruite, et laquelle est renforcée, d’où le changement de couleur lors de l’orientation du billet.
Ces encres sont utilisés sur d’autres éléments également, notamment tout ce qui peut nécessiter une protection anti-contrefaçon (cartes bancaires, tickets restaurants, par exemple), ou des objets suffisamment qualitatifs pour bénéficier d’un élément fantaisiste comme une encre qui change de couleur (pochette de CD, clés USB, cartes de collection…).
Enfin, certaines encres peuvent également changer de couleurs sous l’effet d’un courant électrique, de la chaleur ou de rayonnement ultraviolet. Dans ce cas, ces différents paramètres (courant, chaleur, UV) modifient physiquement ou chimiquement le processus de production de la couleur. Dans le cas des couleurs qui changent sous la chaleur, par exemple, c’est l’espèce chimique qui est altérée : la molécule elle-même est modifiée et change de couleur sous l’effet de la chaleur.
Ressources
- Encre optiquement variable – Wikipédia ;
- What is Optically Variable Ink (OVI)? | Document Glossary ;
- Counterfeit protection with OVI - find alternatives.
image d’en-tête : travail personnel.
Comment fonctionnent les détecteurs de pluie sur un parebrise ?
Couleur science par Anonyme le 03/04/2025 à 05:47:00 - Favoriser (lu/non lu)

Un autre objet du quotidiens dans lequel l’on utilise de la science, ce sont les détecteurs de pluie sur les parebrises des voitures. Je parle ici des véhicules qui activent ou désactivent les essuies-glaces de façon automatique, dès qu’il se met à pleuvoir ou que ça s’arrête.
Il existe plusieurs techniques pour ça : détecteur par ultra-sons, par capteur d’humidité, mais le plus utilisé aujourd’hui est le capteur par infrarouge.
Il est intéressant de noter que ces techniques sont très récentes (post-2000), mais la recherche d’une méthode de déclenchement automatique ne date pas d’hier. Ainsi, en 1970, les ingénieurs chez Citroën avaient, pour la Citroën SM, déjà inventé un système pour cela. Ce fut un système entièrement électro-mécanique, sans électronique ni ordinateur de bord et encore moins de caméras.
Un capteur primitif par Citroën en 1970
Le fonctionnement recherché était le suivant : tant qu’il pleuvait, les essuie-glace — préalablement activés manuellement — devaient continuer de tourner. Dès que la pluie cessait, ils devaient s’arrêter tout seul.
Le principe de fonctionnement reposait sur la variation de la force de frottement des essuies-glaces : ces derniers glissent plus facilement sur le pare-brise mouillé lorsqu’il pleut, que sur un pare-brise sec.
Activés initialement, donc, les essuie-glace continuaient de tourner tant qu’ils glissaient bien sur l’eau de pluie. Mais dès que la pluie cesse, le pare-brise reste sec et la force nécessaire pour les faire tourner augmente : c’était alors signe que ces derniers pouvaient être coupés.
Le système intégrait une résistance chauffante ferromagnétique sous la forme d’un contacteur et placé en série avec le circuit d’alimentation du moteur actionnant les essuie-glaces. L’ensemble était placé à proximité d’un aimant.
Par temps de pluie les essuie-glace glissaient bien, le moteur électrique ne forçait pas et tirait un courant électrique raisonnable : le contacteur ne chauffait pas et reste collé à l’aimant. Cette position maintenait les essuie-glaces actifs.
Lorsque la pluie cesse, les essuie-glace frottent davantage. Il en résulte que le moteur force et tire plus de courant. Par effet joule, le contacteur résistif placé en série s’échauffe alors. Il chauffait au point de dépasser sa température de Curie ; la température au-delà de laquelle un matériau perd sa perméabilité magnétique : en d’autres termes, il perd ses propriétés magnétiques.
Ainsi, le contacteur chauffé n’était plus attiré par l’aimant, il s’en décolle et ouvre le circuit. Le contacteur était ensuite replacé dans sa position au repos et le commodo au volant également. Le mécanisme terminait le cycle de balayage des essuies glaces et s’arrêtait ensuite, tout seul. Ingénieux !
Ce système était resté relativement unique pour l’époque mais le marché de la Citroën SM n’était pas suffisant pour l’implémenter ailleurs ; il était compliqué pour un avantage somme toute léger.
Aujourd’hui, plus aucun système ne fonctionne comme ça. Tout passe par de l’électronique, des LED infrarouges ou des ultrasons. Ces systèmes récents sont plus fiables, plus légers et s’intègrent mieux dans tout le reste de l’électronique d’une voiture moderne. De plus, ils peuvent aussi s’activer tout seuls, pas seulement se désactiver.
Le détecteur à capteur infrarouge
Parlons ici en particulier du système infrarouge, le plus couramment utilisé. Ce système utilise le principe de la réfraction et de la réflexion d’un faisceau lumineux dans un matériau.
Le dispositif est composé d’un émetteur infrarouge d’une part et d’un capteur infra-rouge d’autre part. L’émission d’un faisceau infrarouge est fait avec un angle de 45 degrés. Le faisceau une fois entré dans le verre, arrive à la surface opposée et est réfléchie dans le verre par l’interface verre-air. Le faisceau rebondit donc constamment dans le verre sans jamais en sortir :

On parle d’une réflexion totale interne. Ce principe est également utilisé dans les fibres optiques pour maintenir le signal lumineux dans la fibre.
La réflexion totale interne est possible si les indices de réfraction des deux milieux (le verre et l’air ici) sont très différents. Plus le rapport des indices est important, plus la part des rayons réfléchie est grande. Si les indices sont trop proches, une part plus importante de la lumière passe dans l’autre milieu et est donc perdue. Cela va nous servir.
À un autre endroit du pare-brise, il y a un capteur. Si tous les rayons émis sont bien réfléchis et maintenus dans la vitre, alors le capteur infrarouge capte toute l’onde et il interprète cela comme une absence de pluie.
Lorsqu’il se met à pleuvoir, des gouttes d’eau se retrouvent sur la vitre. Or l’eau a un indice de réflexion plus proche de celui du verre que ne l’est l’indice de l’air. Il en résulte que les infrarouges vont passer assez facilement du verre vers l’eau. Et une fois dans l’eau, l’infrarouge est soit transmise dans l’air (conditions de réflexion totale non satisfaite), soit renvoyée dans le verre dans une direction aléatoire. Dans tous les cas, les rayons ne sont pas forcément renvoyés vers le capteur et ce dernier reçoit moins de lumière infrarouge :

À l’ordinateur de bord d’interpréter l’absence de détection d’infrarouges et d’activer les essuie-glace en conséquence.
Mieux, en détectant la vitesse à laquelle le capteur infrarouge perd le signal ou bien la force du signal perdu, il peut faire tourner les essuie-glaces plus ou moins vite.
Ressources
Quelques liens :
L’énigme de l’eau dans le vin et du vin dans l’eau
Couleur science par Anonyme le 06/03/2025 à 05:26:00 - Favoriser (lu/non lu)

J’ai déjà fait quelques articles « énigmes », comme celui-ci avec la courbe brachistochrone, ou celui-là avec le ballon à aller chercher dans l’eau le plus vite possible.
En voici une autre :
Nous avons deux verres identiques, l’un rempli de vin et l’autre rempli d’eau.
Prélevons une cuillerée de vin, que l’on verse dans le verre d’eau. Ensuite, on prend une cuillerée du verre d’eau — qui contient désormais également un peu de vin — que l’on reverse dans le verre de vin.
La question est : y a-t-il plus de vin dans le verre d’eau, ou plus d’eau dans le verre de vin ?
Histoire de lever tout ambiguïté :
- les verres sont identiques, ainsi que leur niveau de remplissage ;
- les deux transferts se font avec la même cuillère, et leur remplissage est identique dans les deux cas ;
- le fait que le vin soit composé majoritairement d’eau n’entre pas en considération ici. Le vin, y compris son eau, reste du vin.
On peut évidemment raisonner par le calcul, et on va le faire, mais l’on peut aussi raisonner de façon logique, qui est extrêmement rapide.
Le problème
La raison d’être de cette énigme est que lorsque l’on verse la seconde cuillerée, celle-ci contient de l’eau évidemment, mais également un petit peu de vin issu de la première cuillerée. Un peu de vin retourne donc dans le verre de vin.
La résolution de l’énigme consiste à savoir si cela change quelque chose ou non, et si oui, quoi et dans quel sens.
À priori, on pourrait avoir tendance à dire que puisqu’on retire du vin du verre d’eau, la quantité de vin dans l’eau diminue, mais ça serait oublier les proportions des deux liquides dans la cuillère : si l’on reprend du vin lors du second transfert, il y a moins de place pour l’eau, et l’on verse donc également moins d’eau dans le vin.
De plus, lors des dilutions, il faut prendre en compte les volumes totaux dans lesquelles on dilue, ce qui pour le premier transfert est de 1 cuillère de vin dans un volume de 1 verre augmenté du volume d’une cuillère ! Et le second transfert correspond à un versement dans 1 verre − 1 la première cuillère, auquel on ajoute donc une cuillerée !
Il y a une dissymétrie entre les deux transferts et les deux dilutions.
Au final, la réponse n’est pas aussi simple qu’on le pense au premier abord. Néanmoins, en y repensant une seconde fois, on se rend que la réponse est bel et bien très simple.
La méthode logique
Cette méthode n’a besoin d’aucun calcul.
Dans l’expérience, on met successivement une cuillerée du premier verre dans le second, puis une cuillerée du second verre dans le premier. Les verres, qui ont commencé avec des volumes identiques, finissent donc également avec des volumes identiques. Les volumes échangés entre les verres sont donc nécessairement identiques.
On peut en conclure immédiatement que le volume de vin dans l’eau et le volume d’eau dans le vin sont identiques. Voilà, c’est tout !
Quelques explications quand-même ? Lors du premier transfert, du vin du premier verre finit dilué dans le second verre. Lors du second transfert, il faut considérer la seconde cuillerée : elle contient de l’eau du verre d’eau mais aussi un peu de vin issu du premier transfert (et qui retourne dans le vin). Cette quantité de vin est donc ôtée du verre d’eau, qui contient donc désormais un peu moins d’une cuillère de vin.
Ce « un peu moins d’une cuillère » correspond à la quantité d’eau présente dans la seconde cuillerée : plus on ôte de vin du verre d’eau, moins il reste de place pour de l’eau dans la cuillère. Si l’on laisse moins de vin dans le verre d’eau, on verse donc également un peu moins d’eau dans le verre de vin. Peu importe que l’on homogénéise ou non.
C’est infaillible. Cela fonctionne quelle que soit la taille de la cuillère, tant qu’elle reste plus petite que le verre.
La méthode analytique
Passons maintenant au calcul, et vous verrez que l’on retombe sur le même résultat. Pour commencer, il s’agit de mathématiser le problème.
Dans tout le problème on va raisonner en quantités de vin ou d’eau, et donc en volume.
Notons :
- V le volume d’un verre ;
- C le volume de la cuillère ;
- Veau, Vvin et Cvin correspondent aux volumes des verres d’eau, de vin et à une cuillère de vin, respectivement.

Initialement dans les verres, on a : Veau = Vvin.
Effectuons à présent le premier transfert. Il s’agit de prendre une cuillère de vin et de la diluer dans le volume du verre d’eau. Après cette opération, le volume V’ de liquide dans les verres d’eau et de vin sont, respectivement :
$$\begin{aligned}V'_{eau} &= V + C \\ V'_{vin} &= V - C\end{aligned}$$

Le rapport du volume de vin dans le verre d’eau est égal au volume de vin sur le volume total (verre eau + cuillerée de vin) :
$$R_{v/e} = \frac{C}{V+C}$$
De façon similaire, le volume complémentaire dans le verre d’eau est occupé par l’eau seule, dont la quantité est :
$$R_{e/v} = \frac{V}{V+C}$$
Faisons désormais le second transfert, donc la cuillerée du mélange eau+vin se trouvant dans le verre d’eau. Cela se fait en deux étapes : le prélèvement depuis le verre d’eau, et le versement dans le verre de vin.
Le prélèvement : que contient cette cuillerée ?
L’on prend une cuillère du mélange eau+vin se trouvant dans le verre d’eau : ce liquide est identique à celui dans le verre d’eau, et il contient à la fois de l’eau et du vin, dans des proportions égales à Rv/e exprimé précédemment.
La quantité d’eau — juste l’eau, excluant donc le vin — dans la cuillère est égale au volume d’une cuillerée multipliée par ce rapport :
$$\begin{aligned}V_{c_{eau}} &= C \times R_{e/v} \\ &= C \times \frac{V}{V+C} \\ &= \frac{C \times V}{V+C}\end{aligned}$$
Le reste de la cuillerée correspond au vin qui retourne dans le verre de vin. On n’a pas besoin de calculer quoi que ce soit avec ça.
Le versement : comment termine le verre de vin ?

Versons cette cuillère dans le verre de vin, et cherchons à exprimer combien il y a ensuite d’eau dans le verre.
Pour calculer le rapport final d’eau dans le verre de vin, R’e/v$, on considère le volume d’eau dans la cuillère que l’on divise par le volume total du verre de vin, après le transfert, donc tout à la fin de l’expérience.
Rappelons que le volume de vin restant dans le verre avant le second transfert est [b]V−C. À ce volume, on ajoute la seconde cuillerée. Le volume dans le verre de vin après le second transfert est V−C+C, soit simplement V, le volume de départ.
Le rapport du volume d’eau dans le vin est égale au volume d’eau seul dans la cuillère $V_{c_{eau}}$, sur le volume total du verre de vin :
$$\begin{aligned}R’_{e/v} &= V_{c_{eau}} \times \frac{1}{V} \\ &= \frac{C \times V}{V+C} \times \frac{1}{V} \\ &= \frac{C}{V+C} \\ &= R_{v/e} \end{aligned}$$
… et l’on constate que l’on retombe bien sur le rapport de vin dans le verre d’eau, et donc que les rapports d’eau sur vin et vin sur eau sont égales :
CQFD.
Remarques
On peut se demander comment ces rapports peuvent être égaux à $\frac{C}{V+C}$, sachant que la quantité transférée est au final bien inférieur à C[/C].
En fait, on peut voir ces deux transferts « compliqués » d’une cuillerée par le transfert « simple » d’une cuillère plus petite, mais sans mélange entre les deux transferts. C’est-à-dire que l’on prend deux cuillères, une d’eau pure, une de vin pur, puis que l’on verse les deux cuillères dans l’autre verre.
Ces transferts ne s’influencent donc pas l’une l’autre, et la petite partie de vin dans la seconde cuillerée peut être ignorée dans le problème. Ensuite c’est simplement une question de proportionnalité : si l’on peut faire ça avec une petite cuillère, on peut le faire avec une grande, de volume [b]C, et cela restera vrai.
Une chose intéressante à faire lors de ce genre d’expérience (ici, mais aussi de façon générale en sciences), est de raisonner sur les extrêmes. Par exemple, ici, il s’agit de se demander ce qui se passe avec une infinité de transferts alternativement du premier verre vers le second, puis du second vers le premier. Si l’on fait ça, on comprend de façon assez intuitive que les deux verres finiraient par contenir le même mélange 50/50 d’eau et de vin, à cause des transferts successifs et en nombre infini.
Un autre raisonnement serait de voir ce qu’il arriverait avec une cuillère de volume égale à celui du verre. Dans ce cas, lors du premier transfert, la totalement du vin finirait dans la totalité de l’eau, et si l’on homogénéise, alors la totalité du liquide sera homogène à un mélange 50/50 d’eau et de vin. Après le deuxième transfert, on recrée deux verres de volumes égales d’un même liquide composé à 50 % d’eau et à 50 % de vin.
Enfin, un dernier exemple serait une cuillère infiniment petite, qui prendrait une seule molécule d’eau, ou une seule molécule de vin. Le premier transfert serait alors forcément de mettre une unique molécule de vin dans l’eau.
Le second transfert peut se faire de deux manières :
- soit la cuillère récupère une molécule d’eau qu’elle va placer dans le verre de vin, et dans ce cas l’on a une molécule d’eau dans le vin et une molécule de vin dans l’eau, donc des concentrations identiques ;
- soit on n’a pas de chance (ou alors beaucoup), et la seconde cuillerée récupère la seule molécule de vin qu’elle vient d’y mettre, et qu’elle remet alors dans le vin. Finalement, là aussi, on a donc autant d’eau dans le vin que de vin dans l’eau, nonobstant que « autant » signifie alors ici « aucun », et pour les deux verres.
Comment représenter une couleur : les formats standards de la CIE : XYZ, Lab, Lch
Couleur science par Anonyme le 03/02/2025 à 20:19:00 - Favoriser (lu/non lu)

- Comment représenter une couleur : les formats trichromiques, RGB et CMY ;
- Comment représenter une couleur : les formats cylindriques, HSV et HSL ;
- Comment représenter une couleur : les formats employant la luma, Y’UV et dérivés ;
- Comment représenter une couleur : les formats standards de la CIE, XYZ, Lab, Lch (le présent article)
Dans les parties précédentes, on a vu les espaces de couleur cartésiennes (RGB, CMY…) et cylindriques (HSV, HSL…). L’on a aussi vu les formats basés sur le Y’UV, issues d’astuces pour transmettre et afficher des couleurs pour la télévision couleur. Ces espaces sont bien moins intuitifs, mais pour l’ordinateur cela ne change rien.
Tout ceci fonctionne, et même si les systèmes trichromatiques ont une logique similaire à l’œil, elles n’en reflètent pas la sensibilité ni la perception, ni même la psychologie.
Le système HSL est plus proche de la logique de définition d’une couleur que le RGB, mais ce n’est pas tout. L’œil est, par exemple, beaucoup plus sensible au vert qu’au bleu. À éclairement égal (en watt/m²), une lampe verte sera donc perçue plus lumineuse qu’une lampe bleue. Qui plus est, certaines couleurs que l’œil voit ne sont pas codables dans l’espace RGB (ni HSL).
Pour avoir un système de colorimétrie qui se rapproche de la vision humaine, il faut autre chose que le RGB ou les autres formats mentionnés ci-dessous.
De la réponse des cônes au LMS, puis au format XYZ
Dans les années 1930 la Commission International de l’Éclairage (CIE) décide de travailler sur un système de représentation des couleurs à des fins de standardisation.
Rappelons pour commencer que l’œil est sensible aux couleurs par l’intermédiaire de cellules photosensibles appelées cônes, dont il existe trois types sensibles à trois portions du spectre électromagnétique. Ces portions sont les bandes des longueurs d’ondes courtes (420-440 nm, dans les bleus), moyennes (530-540 nm, jaune-vert) et longues (560-580 nm rouge).
En réalité, les cônes sont sensibles à l’ensemble du spectre, et c’est seulement leur réponse maximale qui se situe dans ces bandes. La réponse d’un cône n’est donc pas une seule raie lumineuse, mais plutôt une courbe entière avec un maximum. Les travaux de la CIE porte sur la détermination de ces courbes.
La CIE lance donc une grande étude, avec un grand nombre de personnes à qui l’on demande, par exemple, de reproduire une couleur de référence en ajustant les intensités de trois couleurs primaires se situant dans les longues, moyenne et courtes longueurs d’ondes décrite ci-dessus. On parle aussi des références long, medium et short en anglais, soit L, M, S, ou LMS.
Il résulte de cette expérimentation les trois courbes suivantes, appelées fonctions colorimétriques, qui représentent la sensibilité des trois types de cônes en fonction de la longueur d’onde, pour un observateur standard :

On peut constater sur ces courbes qu’une partie de l’une est située dans les négatifs. Dans l’expérience cela se traduit par le devoir d’ajuster la couleur de référence faute de pouvoir ajuster les trois autres couleurs convenablement. Cette partie négative rend les calculs compliqués. La représentation « LMS » est donc ajustée pour obtenir trois courbes positives. On réalise cela en multipliant les coordonnées LMS par des coefficients, nous donnant alors un nouvel espace de couleur « XYZ » :
$$ \begin{bmatrix}X\\Y\\Z\end{bmatrix} = \begin{bmatrix} C_a & C_b & C_c \\ C_d & C_e & C_f \\ C_g & C_h & C_i \end{bmatrix} \begin{bmatrix} L\\M\\S\end{bmatrix}$$
Et donc de nouvelles fonctions colorimétriques :

Précisons qu’autant les fonctions LMS correspondent directement à la réponse de l’œil à de vraies longueurs d’ondes, celles du XYZ sont obtenus après l’application de la matrice de conversion par le calcul. Il n’y a pas de lumière « X », « Y » ou « Z » qui donne ces courbes, cela n’a même aucun sens. Cela n’empêche pas, mathématiquement, de travailler avec, et c’est ce qui nous intéresse ici.
Autre remarque : mathématiquement, il existe une infinité de matrices de coefficients de conversion applicable sur LMS pour obtenir trois courbes positives. Il en a donc été déterminé une qui soit plus utile que les autres, à savoir celle qui fait correspondre la luminance totale directement sur l’une d’entre elles, en l’occurrence la coordonnée Y. Les trois coordonnées vont toujours correspondre (à une matrice de constantes près) à trois stimuli lumineux, mais la coordonnée Y va, en plus, correspondre à la luminance totale. C’est la magie du calcul matriciel :
$$ \begin{bmatrix}X\\Y\\Z\end{bmatrix} = \begin{bmatrix} 1.91020 & -1.11212 & 0.20191 \\ 0.37095 & 0.62905 & 0 \\ 0 & 0 & 1.00000 \end{bmatrix} \begin{bmatrix} L\\M\\S\end{bmatrix}$$
Ce Y pour la luminance donnera, dans les années 1950, le Y au Y’UV vu dans l’article précédent. Y’UV aussi note sa luminance sur un Y, et non sur un L, qui aurait pu sembler plus naturel.
L’espace XYZ donc donne :

Ce diagramme représente toutes les teintes capables d’êtres vues par l’œil. Un tel diagramme, qui représente l’ensemble des couleurs d’un modèle colorimétrique est appelé gamut.
Le pourtour du haut, avec sa forme caractéristique de fer à cheval, s’appelle le le lieu du spectre. Il comporte les longueurs d’ondes du spectre visible. Cette courbe contient donc les couleurs que l’on peut obtenir avec une seule longueur d’onde. Toutes les autres couleurs du diagramme ont besoin de deux ou plus de longueurs d’ondes pour être produites.
Le segment du bas qui relie le les deux extrémités du spectre (le rouge et le bleu) s’appelle la droite des pourpres. On y trouve le magenta, notamment.
On constate un point blanc plus ou moins au centre du diagramme : ce point est appelé le point blanc, et il est la couleur obtenue avec une émission identique dans les 3 couleurs de référence. Ce point est très important en colorimétrie et beaucoup de calculs doivent le prendre en compte.
Le point blanc va dépendre de l’illuminant : une lumière de référence pour l’éclairage de la surface dont on veut évaluer la couleur. Rappelons que le CIE veut rendre compte des couleurs perçues par l’œil humain, or notre perception des couleurs dépend de l’éclairage ambiant. Pour caractériser la couleur d’un objet, il faut donc également spécifier comment on l’éclaire. La normalisation est quelque chose de compliqué, oui, mais ce sont là des choses qui servent dans le domaine de la photographie et du cinéma, mais aussi la création de peintures, de teintes, de pigments, et évidemment donc dans tous les secteurs qui y recourent.
Il existe plusieurs illuminants : le plus employé correspond à la lumière du Soleil en plein jour, qui est la lumière émise par rayonnement d’un corps à 6 500 kelvins filtré par notre atmosphère. On l’appelle « D65 », pour Daylight 6 500 K. Il en existe un paquet d’autres, qui vont représenter le spectre émis par un émetteur uniforme (E), une LED (LED-B1, LED-LH1…), la lumière du ciel de l’hémisphère nord (C), un filament de tungstène (A)…
L’observateur devra de plus se trouver dans un angle précis par rapport à la surface et l’éclairage. Généralement on parle de 2°, parfois aussi 10°. En colorimétrie, il ne sera donc pas rare que l’on considère un éclairage de type « D65 10° » par exemple. Pour vérifier qu’une peinture produit bien la couleur demandée, on l’éclaire donc avec un illuminant D65 sous 10° et on compare avec la teinte demandée.
Le sRGB
Le XYZ RGB, qui sert de référence aux sRGB est une sous partie du XYZ. Il s’agit d’un triangle situé dans l’espace XYZ, avec trois sommets représentant les couleurs de références (R, G, B) :

Ce sRGB est celui qui sert de référence aux écrans depuis 1999. Avant, l’on utilisait le standard PAL et NTSC sur les écrans cathodiques. Le sRGB est également ce qui est utilisé dans les pages web. Ce standard, comme tous les standards, permettent une harmonisation des couleurs d’un écran à un autre, et font qu’un « orange-vif » affiché sur un PC montre la même couleur lorsqu’elle est affichée sur un projecteur, une télé ou un smartphone.
On peut faire la remarque que si le sRGB est une sous partie de XYZ — qui représente tout ce que l’œil peut voir — alors le sRGB ne contient pas toutes les couleurs visibles. Pour le dire autrement : les implémentations du sRGB sont incapables de reproduire certaines des couleurs visibles par l’œil ; ou encore que l’œil voit plus de couleurs que ce qu’un écran ne peut afficher.
Certaines couleurs de la vie courante sont donc impossibles à mettre sur un écran. En fait, le sRGB, ne couvre que 35 % environ des couleurs visibles par l’œil. On peut se dire que ce n’est pas un problème, mais l’on verra dans quelques dizaines d’années qu’un couvrant tout le gamut du visible sera une avancée aussi grande par rapport au sRGB que la télévision couleur fut par rapport à la télévision en niveaux de gris.
Une limite de praticité sur le format XYZ
On remarque qu’une très large partie de l’espace de couleur XYZ est prise par le domaine des verts. La raison est liée à la fonction colorimétrique du vert, dont le pic est assez large, ainsi qu’à la lumière du Soleil, dont le maximum du spectre se trouve dans le vert (et donc l’œil qui s’est très largement adapté à ça).
Cette grande portion de vert semble uniforme : deux points dans cette zone seront perceptuellement très similaires, là où des couleurs identiquement proches dans le reste du domaine donnent des couleurs très différentes. Cette différence de perception d’un bout à l’autre du diagramme constitue un casse-tête dans les calculs, par exemple pour trouver des couleurs complémentaires, similaires, ou de clarté comparables.
On ne peut pas prendre deux points équidistants sur le gamut XYZ et s’attendre à ce que les variations de couleurs soient identiques. Au contraire : les deux couleurs seront presque identiques dans le vert, mais très différentes ailleurs.
Les normes CIE Lab et CIE Luv ont donc été créées (bien plus tard, en 1976) pour corriger cette particularité et faciliter les travaux de colorimétrie, notamment pour l’informatique et l’affichage des couleurs alors naissant pour un usage grand public.
CIE Luv & CIE Lab
Ces deux formats sont la suite du XYZ : ils couvrent à nouveau toutes les couleurs perceptibles par l’œil humain, et font également la distinction entre la chromaticité (la couleur, la teinte) et luminance (la luminosité, la clarté).
On a vu que dans le XYZ, lorsque l’on modifie une des coordonnées, donc lorsque l’on se déplace sur le diagramme, pour un même déplacement, le changement de couleur perçue n’est pas constant. Un même déplacement n’a donc pas toujours les mêmes écarts perceptuels :

La CIE L*u*v*, ou Luv et la CIE L*a*b*, ou Lab, veulent corriger ça. Les diagrammes sont remodelés de façon à uniformiser la distribution des teintes de couleur. Le Luv et le Lab étirent les domaines rouges et bleu de l’espace XYZ, ce qui recentre le point blanc, qui était un peu bas dans le XYZ. Il s’agit à nouveau d’une transformation matricielle (tout comme l’on était passé du LMS au XYZ).
Le Lab utilise le même domaine, mais y place les axes différemment, plutôt selon les axes rouge-vert et jaune-bleu et plaçant l’origine au milieu :

Le Lab et le Luv se distingue essentiellement dans la nature de leur emploi : le Luv est utilisé pour les sources lumineuses et les écrans, donc pour une logique d’émission (donc additive) de la lumière, alors que le Lab est utilisé pour les colorants, pigments et les surfaces, donc une logique d’absorption (ou soustractive) de la lumière.
En dehors de cela, le Lab et le Luv sont la même chose que le XYZ, c’est juste la façon de les représenter qui change.
Et CIE LCh ?
On rencontre également les espaces CIE L*C*h, ou LCh. Ici, le L est identique au L du Lab, mais les a et b sont remplacées par le chroma C et la teinte h.
Il s’agit ici simplement d’une représentation en coordonnées polaires de l’espace Lab.
On peut dire que le LCh est au Lab, ce que le HSL est au RGB.
On distingue la transformation LCh appliquée au Lab de celui appliqué au Luv, et on note tout ça : LChab et LChuv.
Les espaces Lab/Luv et LCh ab/uv couvrent les mêmes espaces, et seule la façon de les représenter est modifiée, et chacun ont donc des applications différentes (selon l’emploi, ou la logique de calcul recherché).
Attention : la valeur de la teinte — le h — donnée dans l’espace LCh et celui du H dans HSL sont différentes. Quant à ce qu’on appelle le « chroma » du LCh, il s’agit d’un analogue — mais pas identique — à la saturation en HSL, c’est-à-dire la quantité de couleur, par rapport à la quantité de lumière (on parle de la pureté d’excitation de la couleur pour l’œil).
OkLab et OkLCh
OkLab est une nouvelle itération évolutive sur le domaine du XYZ : « Ok » étant pour « Optimal [k]olors », sorti seulement en 2020.
Si le Lab (et le Luv) lisse les perceptions des teintes par rapport au XYZ, OkLab lisse la perception de la luminance et de la saturation.
En effet, que ce soit en HSL ou en Lab, deux couleurs avec la même luminance peuvent être perçues comme plus ou moins lumineuses ou « éclatante » malgré tout. À nouveau, il s’agit d’une particularité de l’œil et du cerveau.
Ainsi, dans le gamut du HSL, on a toutes les couleurs de 0 à 360°. On peut constater une luminosité très forte sur les jaunes, et plutôt faible sur les bleus. Avec le OkLab (ou OkLCh), toutes les couleurs voient leur luminosité uniformisée :

Bien-sûr, on pourra toujours obtenir des jaunes moins lumineux et des bleus clairs, mais pour ça il faudra ajuster la clarté, le « L » dans OkLab. Toutes les couleurs descendront ou monteront en même temps pour conserver l’uniformité sur un spectre complet. Pour obtenir une même luminosité en changeant la couleur, une seule coordonnée doit changer, alors qu’il fallait en modifier deux avec le HSL.
OkLab ou OkLCh sont également utiles lorsque l’on cherche à faire des dégradés : toutes les couleurs du dégradé seront de luminance égale et le dégradé sera particulièrement lisse.
Enfin, l’un des derniers points en faveur de OkLab ou OkLCh, c’est qu’ils supportent plus de couleurs que RGB (ou HSL). Ces derniers se limitent à 16,7 millions de couleurs, mais OkLab et OkLCh en proposent beaucoup plus de façon à assurer une couverture un peu plus grande du gamut XYZ dans son ensemble.
Et la norme P3 ?
Comme je l’ai dit plus haut pour le sRGB par rapport au XYZ, le premier ne couvre que 35 % du second. Or, le sRGB est ce qui est utilisé pour nos écrans. Ces derniers ne peuvent donc reproduire que 35 % de toutes les couleurs visibles par l’œil humain.
La nouvelle norme née en 2005, la DCI-P3, mise au point par des industriels du cinéma, devrait remplacer peu à peu le sRGB. La norme P3 couvre 53,6 % de la CIE XYZ, ce qui représente environ 40 % de couleurs en plus par rapport au sRGB. Un écran capable de ça affichera donc beaucoup plus de couleurs :

Bien-sûr, afficher une de ces « nouvelles » couleurs sur un écran en sRGB ne sera pas possible : il ne sera affiché que la couleur la plus proche. Ça sera un peu comme si l’on jouait un DVD couleur sur un écran en noir-et-blanc : l’image sera tout à fait visible et s’affichera, elle sera juste bridée par les limites du système d’affichage.
Aussi, une de ces nouvelles couleurs ne pourra s’afficher avec la représentation rgb() que l’on a vu précédemment. Il faudra utiliser une nomenclature capable d’encoder plus de 16 millions de couleurs (donc plus de 24 bits).
Le Oklab (et même le Lab) ainsi que leur pendant en coordonnées polaires (OkLCh, LCh) sont capables de cela. Afficher une couleur en OkLab sur un écran compatible P3 vous montrera donc une de ces couleurs.
Certains appareils supportent déjà tout ça, en particulier le matériel Apple comme l’iPhone, ou les téléphones Pixel 3 et ultérieurs de chez Google.
En pratique, les couleurs affichées sont beaucoup plus vives, très claires et très brillantes. Toute couleur RGB, même la plus pure, paraît terne à côté. Vous pouvez tester cela ci-dessous :
| Couleur Oklab/P3 | Couleur sRGB |
|---|---|
| oklch(100% 0.212 179) | #00FFFF |
| oklch(96% 0.4 108) | #FFF900 |
| oklch(96% 0.4 137) | #17FF00 |
| oklch(96% 0.4 46) | #FF5000 |
| oklch(100% 0.4 0) | #FF20F4 |
Conclusion
Les formats du CIE sont là pour approcher ce que l’œil voit. Et justement, ce que l’œil voit, a été mis en équation par des études sur des sujets humains « moyens » dans les années 1930. Le but était d’avoir une représentation mathématique et chiffrée des couleurs visibles par un être humain, et de constituer un référentiel normatif pour la notion de couleur. Les couleurs sont tout autour de nous, du rouge « coca-cola » dans les publicités, aux encres pour les imprimantes, en passant par les tubes de peintures, des papiers photos et les écrans.
Le format de base mis au point par la CIE est le XYZ. Des évolutions sont venues ensuite en 1978 puis en 2020 avec le Lab/Luv puis le OkLab afin d’apporter des corrections et des améliorations et ainsi étendre les possibilités techniques de leurs applications (écrans, pigments…).
Cet article explicatif conclut cette série d’articles sur les couleurs et la manière de les représenter, que ce soit en informatique, ou dans l’industrie en général pour toutes les applications que l’on peut imaginer.
Il existe encore plein d’autres de formats de couleur et même d’espaces de couleurs, plus ou moins utilisés, plus ou moins propriétaires (Adobe RGB, Apple P3, etc.), mais ceux présentés ici me semblaient être les plus courants et les plus intéressants à présenter.
Ressources
- Wide Gamut Color in CSS with Display-P3 | WebKit ;
- The CIE XYZ and xyY Color Spaces, Douglas A. Kerr ;
- Comparative analysis of color models for human perception and visual color difference ;
- Perceptual color models | Chromatone.center ;
- Color space - MDN Web Docs Glossary: Definitions of Web-related terms - MDN ;
- Colorimétrie - Systèmes CIELAB et CIELUV ;
- Couleurs : théorie - le guide de l'éclairage ;
- Fundamentals of Imaging Colour Spaces, Prof. Dr. Charles A. Wüthrich, Bauhaus-Universität Weimar ;
- LMS color space - Wikipedia ;
- CIE 1931 color space - Wikipedia ;
- Interactive post on OKLCH color space | Little Things.
Comment représenter une couleur : les formats employant la luma, Y’UV et dérivés
Couleur science par Anonyme le 03/02/2025 à 20:18:00 - Favoriser (lu/non lu)

- Comment représenter une couleur : les formats trichromiques, RGB et CMY ;
- Comment représenter une couleur : les formats cylindriques, HSV et HSL ;
- Comment représenter une couleur : les formats employant la luma, Y’UV et dérivés (le présent article) ;
- Comment représenter une couleur : les formats standards de la CIE, XYZ, Lab, Lch.
Précédemment, on a vu les espaces de couleur cartésiennes (RGB, CMY…) et cylindriques (HSV, HSL…). Ces deux systèmes tirent leur origine d’une logique physionomique et psychologique, respectivement, de la perception des couleurs. Le RGB et le CMY utilisent un système à base de trichromie qui reflète la trichromie de l’œil, et les espaces cylindriques utilisent la façon que l’on a de définir une couleur de façon intuitive (teinte, puis éclat ou luminosité).
Dans certains cas, cela ne suffit pas. Parfois, ce sont les contraintes techniques qui nous obligent à inventer des systèmes de couleur un peu moins direct ou intuitifs.
Espaces de couleurs utilisant la luma
Dans le cas qui va suivre, il a été utilisé à nouveau un système qui distingue d’un côté la luminosité d’une couleur (son intensité), et de l’autre sa chromaticité, c’est à dire sa teinte. Cette dernière est désormais codée sur deux axes, en coordonnées cartésiennes.
La particularité est que le choix des couleurs semble ici totalement arbitraire, a priori pas du tout logique : les axes du YUV par exemple vont du rose au turquoise et l’autre du violet au vert-orange. La position sur ce diagramme permet de reconstituer n’importe quelle couleur quand-même, mais cela semble peu naturel. La raison est mathématique, et l’on va détailler tout ça maintenant.
Représentation YUV
Parlons par exemple de la représentation YUV (ou Y’UV, plus précisément).
Ce format est né avec la télévision couleur. Avant cela, quand il n’y avait que de la télévision en niveaux de gris, les pixels n’avaient pas de sous-pixels. Chaque pixel était simplement plus ou moins éclairé et cela donnait une nuance de gris.
Le signal télévisuel était transmis sur des ondes, et ces ondes n’encodaient donc que la valeur de l’éclairement pour chaque pixel :
- pixel #1 : 10 %,
- pixel #2 : 55 %,
- …
Ces valeur — 10 % et 55 % ici dans l’exemple — sont appelées la luminance relative. Il reflète la quantité de lumière que doit émettre ce pixel.
Sauf que les dispositifs de rendu d’image de l’époque étaient des tubes cathodiques qui envoyaient un faisceaux d’électrons sur les luminophores pour les exciter et les rendre lumineux. Or, ni les canons à électrons, ni les luminophores sur les pixels ne répondaient linéairement à leur excitation : ce n’est parce qu’on mettait 50 % de tension sur le canon que le pixel visé renvoyait 50 % de sa luminosité maximale.
Il fallait apporter un correctif, appelé correction de gamma. Ce correctif dépend du support utilisé : un canon à électron avec des pixels ici, mais le même problème est rencontré en photographie, où les films argentiques et les filtres colorés n’avaient pas tous le même rendement. Ce correctif permet de redonner le bon contraste à une image en reliant la luminosité du photophore de l’écran à la valeur réelle du signal à transmettre dans l’onde.
Les grandeurs auxquels on applique une correction gamma sont annotés d’une apostrophe, ou d’un prime « ’ ». C’est pour ça que le « YUV » devient « Y’UV ». Cela ne change rien pour le principe du Y’UV, mais explique cette notation, très largement répandue.
Pour en revenir à notre écran en niveaux de gris, le signal transmis était le Y’ : c’est le signal de luminance corrigé de gamma, que l’on appelle « luma ». Juste lui, car c’est tout ce que le poste de télévision avait besoin en information pour les pixels pour restituer une image en niveau de gris.
Quand maintenant la télévision couleur est apparue, avec des sous-pixels rouges, verts, bleus (pris par mimétisme de l’œil), on aurait pu utiliser trois signaux : R’, G’ et B’. Mais que faisait-on des vieilles télés noir-et-blanc ? Avec un signal R’G’B’, ils ne pourraient rien faire. Et il n’était ni envisageable d’exiger de tout le monde de changer de télé, ni d’envoyer les signaux deux fois.
La solution était donc de continuer à émettre le signal de luma, pour tout le monde, et de trouver une astuce pour les couleurs. Cette astuce est de mettre l’information de la couleur, indépendante de la luma, sur deux axes que l’on a appelé U et V. Ces signaux U et V était ignorés par les télés en niveaux de gris.
Ce moyen, utiliser la luma et deux autres coordonnées pour retrouver trois couleurs primaires, est une astuce remarquable donné par un calcul mathématique. Ce calcul est le suivant :
$$\begin{aligned}R’ &= Y’ + V \\ G’ &= (-Y’ - U - V) \\ B’ &= Y’ + U\end{aligned}$$
Comme on voit, une petite jonglerie mathématique qui n’est autre qu’un système d’équations, qui permet d’utiliser un signal déjà existant — le Y’ — pour adapter les nouveaux signaux afin de s’économiser de nouvelles télé pour tout le monde, ou de nouvelles antennes. Brillant.
Notre orange vif, représenté en Y’UV devient :
-
yuv(0,514, -0,203, 0,247).
Les valeurs sont pondérées avec des coefficients dont l’origine est technique (rendements différents selon les luminophores dans les écrans, par exemple), d’où ces valeurs numériques un peu arbitraires.
Que représentent U et V ? Ce sont les signaux de chrominance. Ils transportent donc les informations de la couleur, là où Y’ ne transporte que la luma. Au lieu d’utiliser des pourcentages de rouge, vert, ou bleu comme dans RGB, les U et V correspondent à des coordonnées sur un diagramme de couleur spécifique. En l’occurrence, l’axe U va du vert au violet, et l’axe V du turquoise au rose :

Cet espace de couleur n’est ni moins légitime ni moins fonctionnel que le RGB ou le CMY, mais il n’est pas aussi naturel. Il est purement un résultat mathématique issu de la contrainte de devoir réemployer le signal de luma produite pour les premières télés.
Le Y’UV est utilisé tel quel pour le standard télévisuel PAL, utilisé notamment partout en Europe (hors France), en Chine, en Inde. Le principe du Y’UV a de nombreux dérivés développés pour des standards différents à travers le monde (voir là) :
- Y’IQ, pour le standard américain NTSC (USA, Amérique du Nord, Chili, Japon…) ;
- Y'DbDr pour le standard français SÉCAM (France, Russie, pays issues d’anciennes colonies françaises) ;
- Y’PbPr, pour la HD analogique apparue par la suite ;
- Y’CbCr, pour du signal numérique, y compris au sein du format JPEG ou MPEG (mp4) ;
- …
Le principe reste le même pour tous : la luma Y’ subsiste comme un héritage du passé et est d’ailleurs commune à tous ces standards. Ce qui change ce sont seulement les cartes de couleurs utilisées pour retrouver les signaux RGB. Effectivement : le choix des axes du turquoise au rose ou du vert au violet peut changer. La seule contrainte est de pouvoir obtenir toutes les couleurs avec deux axes, peu importe les couleurs des axes eux-mêmes.
Si l’on continu de l’utiliser aujourd’hui, c’est aussi parce que l’œil humain est plus sensible aux variations de luminosité (grâce aux bâtonnets) que de couleurs (grâce aux cônes, pourtant plus nombreux). On encode donc en général plus d’information dans la luma que dans la chrominance (c’est ce que fait très largement JPEG, par exemple, pour compresser les images et gagner de la place).
Voici ce que cela donne pour une même image, décomposée des différentes façons :

Amélioration supplémentaire : Y’IQ
Avec le Y’UV, on s’économise des installations de nouvelles antennes pour la télé couleur en plus d’antennes pour les télés « noir-et-blanc ». Il s’agit d’une astuce technique qui a permis le passage à la télé couleur sans arrêter de transmettre pour les anciennes télé.
D’autres astuces peuvent être utilisées, et le Y’IQ emploie l’une d’elle. Le Y’IQ utilise le même luma Y’, et même le même diagramme de chrominance. Seulement, il fait faire une rotation de 33° au diagramme (et une inversion en miroir) :

L’intérêt de ceci est que l’œil est plus sensible aux variations entre l’orange et le bleu qu’aux variations entre le violet et le vert. En utilisant un diagramme de chrominance dont les axes suivent les domaines orange-bleu (I) et violet-vert (Q), on peut choisir de réduire la quantité de données à transmettre sur l’axe Q. Pour résumer, on dégrade le signal sur un des canaux où l’œil est moins sensible. L’œil ne verra pas de différence, mais le signal sera transmis en consommant moins de données, et on peut donc utiliser une onde porteuse de fréquence plus faible (synonyme d’onde de plus faible puissance également).
L’inconvénient, c’est que si le signal télé est encodé sur des ondes de différentes fréquences, le poste de télévision doit intégrer la capacité à filtrer différentes fréquences. Cela réduit donc le coût de l’émission des ondes télévisuelles, mais augmente le coût de réception, donc du poste de télévision.
Il s’agit d’une forme de compression (avec perte). Ajoutons qu’on parle ici d’une innovation datant des années 1950 et implémentée dans les télés au standards NTSC. Aujourd’hui, avec le numérique et la télévision numérique (DAB, TNT…), le standard NTSC américain n’est plus utilisé, et le YIQ non plus. En Europe et en France, la télé numérique (TNT) a également totalement remplacé la télé analogique, qui n’est plus émise.
Conclusion
Les formats basés sur la luma utilisent une coordonné pour la luminosité relative (ajustée de gamma), et deux coordonnées pour la couleur. Ensemble, les trois permettent au système analogique de déterminer les trois composantes R, G, B. On en revient toujours au RGB car l’écran des postes de télévision fonctionnent avec des sous-pixels rouges, verts et bleus. Eux-mêmes choisis pour reproduire les cônes des yeux, et aussi parce que produire des luminophores rouges, verts, et bleus est quelque chose que l’on sait faire.
Si les télés avaient été capables de couleur dès le départ, sans jamais avoir été en niveaux de gris, l’on n’aurait probablement jamais utilisé tout ce système, mais directement du RGB.
Toujours est-il que les formats basés sur la luma persistent aujourd’hui, bien après les télés noir et blanc, et même les télés à écran cathodiques en général, au sein des formats d’encodage d’images (JPEG) ou de vidéos (MPEG). Outre leur existence historique, ils permettent des astuces de compression intéressantes, comme réduire le débit de données sur la chrominance sans toucher au débit de données de la luminance, le tout sans recourir à des besoins importants pour le décodage et la restitution de l’image finale.
Aujourd’hui, d’autres systèmes naissent et sont utilisés pour les formats d’encodage et d’affichage de dernière génération : plus compactes, plus intuitifs, et plus étendus, au prix toutefois de la nécessité d’une puissance de calcul parfois plus important (bien que ça ne soit plus tellement une priorité aujourd’hui). Ces formats là font l’objet du quatrième et dernier article de cette série.
Comment représenter une couleur : les formats cylindriques, HSV et HSL
Couleur science par Anonyme le 03/02/2025 à 20:17:00 - Favoriser (lu/non lu)

- Comment représenter une couleur : les formats trichromiques, RGB et CMY ;
- Comment représenter une couleur : les formats cylindriques, HSV et HSL (le présent article) ;
- Comment représenter une couleur : les formats employant la luma, Y’UV et dérivés ;
- Comment représenter une couleur : les formats standards de la CIE, XYZ, Lab, Lch.
Dans le premier article, on a expliqué le format RGB. En RGB, nous sommes partis des trois types de cellules sensibles aux couleurs dans l’œil, les trois types de cônes, qui sont sensibles au rouge, vert et bleu, et nous avons construit un système de couleur imitant cela, c’est-à-dire un système où l’on dose des niveaux de rouge, de vert et bleu pour reconstituer une couleur en miroitant le fonctionnement physiologique de l’œil.
On peut faire autrement. On peut se baser sur la psychologie de la perception des couleurs à la place, non basée sur un mélange de couleurs. Les espaces de couleurs cylindriques sont là pour ça.
Espaces cylindriques : HSV, HSL…
Les espaces RGB ou CMY sont cubiques : les trois couleurs peuvent être représentées dans un repère cartésien « x, y, z », dit cubique, où chaque coordonnée correspond à une couleur.
Les formats qui vont suivre n’utilisent plus un repère cartésien, mais un repère cylindrique : avec angle, rayon, hauteur. Il s’agit d’un arrangement différent des couleurs du RGB (ou du CMY). Ces deux représentations sont bijectifs : ils contiennent les mêmes couleurs et peuvent être converties l’un en l’autre de façon exacte.
L’approche des systèmes cylindriques dont on va parler est issue de la psychologie humaine : généralement, on ne jauge pas les quantités de R, G, B à mélanger lorsqu’on veut choisir une couleur. À la place, on va plutôt choisir une famille de couleurs (les bleus, les oranges…) puis choisir une teinte plus ou moins foncée ou claire, vive ou terne dans cette famille de couleurs, et enfin une luminosité, claire ou sombre.
Cette approche-là, plus proche de la vie courante, est ce qui est utilisé ici. En réalité, parmi tous les espaces de couleurs, cette séparation entre couleur (« chrominance ») d’un côté et la saturation/luminosité de l’autre est ce qui se fait de plus. La séparation trichromique du RGB fait plutôt figure d’exception.
Construction du système HSV
Le format « HSV » est un format cylindrique très utilisé. Voyons comment on peut essayer de le reconstruire.
Partons des couleurs de l’arc-en-ciel, du spectre de la lumière blanche :

Sur ce spectre, l’on devine les positions des couleurs rouges, vert, bleu, ainsi que le cyan et le jaune. Mais qu’en est-il du magenta ?
Le magenta n’existe pas sur l’arc-en-ciel ! Et ce n’est pas la seule couleur : le rose, le blanc, le gris, ou le marron n’y sont pas non plus. Ces couleurs sont des constructions du cerveau. Si le jaune ou le bleu peuvent être obtenues avec une seule longueur d’onde, le magenta ou le marron sont obtenues par la perception simultanée de plusieurs longueurs d’ondes (et donc l’excitation de plusieurs cônes en même temps).
Le magenta en particulier est obtenu par un mélange de bleu et de rouge. Incidemment, il s’agit des deux extrémités du spectre de la lumière blanche. On peut recourber le spectre sur lui-même de façon à en faire rejoindre les deux extrémités, et y placer le magenta. L’on obtient est alors un cercle chromatique :

Chaque teinte de couleur est représentée par un angle sur le cercle. Les couleurs fondamentales sont placées à 0° (rouge), 120° (vert) et 240° (bleu). Automatiquement, on aura les couleurs primaires à 60° (jaune), 180° (cyan) et 300° (magenta).
Évidemment, ici, l’on n’a que des couleurs de base, que des « teintes ». Si l’on en souhaite les variantes sombres/claires, ou ternes/vives, il faut des coordonnées en plus.
Si l’angle de la teinte est le premier paramètre, le deuxième peut-être la saturation : on peut voir ça comme son intensité. Une couleur intense est alors vive, au contraire d’une couleur terne, grise, délavée.
Le cercle chromatique à une seule dimension devient alors un disque chromatique, où chaque couleur est représentée par des coordonnées polaires. L’angle représente la teinte, et le rayon, sa saturation : plus on s’approche du centre, plus la couleur est terne. Plus on va vers l’extérieur, plus la couleur est vive :

Ceci ne nous permet pas encore tout : il manque la possibilité de choisir le caractère foncé ou claire d’une couleur. Et pour ça, il nous faut le dernier des paramètres. Celui-ci s’appelle la valeur : on peut le relier à sa clarté, sa brillance. Une couleur avec une valeur faible sera proche du noir, alors qu’avec une valeur haute sera pure et éclatante.
Si l’on reste au centre, au niveau des gris, on aura une échelle de gris qui va du noir au blanc.
De cercle, nous étions passés à disque, et désormais de disque, passons à cylindre : le paramètre de la valeur correspond ici à la hauteur sur le cylindre chromatique :

Dans l’ensemble, on a un cylindre complet, et les coordonnées angle, rayon, hauteur donnent respectivement la teinte (rouge, bleu…), la saturation (du gris terne à la couleur vive) et la valeur (la même teinte+saturation, mais sombre ou claire) :
Teinte, Saturation et Valeur — TSV — c’est le nom français pour la représentation HSV (de l’anglais : hue, saturation, value). Le premier paramètre est un angle de 0 à 360°, les deux autres généralement un pourcentage de 0 à 100 % ou bien une valeur entre 0 et 1.
Notre orange-vif de plus tôt donne alors : hsv(30, 87%, 80%). On note que le premier nombre, l’angle, vaut 30°. Si le rouge est à 0° et le jaune à 60°, on comprend que l’orange soit situé exactement entre les deux, à 30°.
Variante HSL
À la place de HSV, on peut trouver HSL : hue, saturation, lightness, soit teinte, saturation, luminosité.
Les deux systèmes sont très proches, et ne diffèrent que par la troisième coordonnée.
Sur le HSV, la hauteur du cylindre montre l’intensité de la couleur à partir du noir. Autrement dit, en partant de rien (pas de lumière), on illumine peu à peu la couleur jusqu’à sa puissance maximale dans sa couleur.
Avec le HSL, cette coordonnée montre la luminosité totale. Si bien que sur une luminosité maximale à 100 % on obtient du blanc. Pour avoir une couleur pleine, la luminosité doit être à 50 %, et on joue ensuite sur la saturation pour aller du gris à cette couleur :

Notre orange-vif se compare en HSV et en HSL alors :
-
hsv(30, 87%, 80%) -
hsl(30 77% 45%)
L’angle de la teinte est la même dans les deux espaces cylindriques, pour chaque couleur.
Variante HWB
Une variante encore plus intuitive est le HWB, pour hue, whiteness, blackness, soit teinte, blanc, noir.
Ce système reprend complètement le principe que l’on aurait avec un set de 5 tubes de peinture : les couleurs primaires avec lesquelles on peut faire toutes les couleurs, ainsi que le noir et le blanc.
En HWB, on choisit notre teinte, et l’on dose ensuite le noir et le blanc pour obtenir la couleur précise souhaitée.
Les doses de blanc et de noir sont notés sur une échelle de 0 à 100 %. Il constitue, en quelque sorte, la quantité de blanc (ou de noir) dans le total, incluant le pigment. Ainsi, avec 100 % de blanc, on a automatiquement 0 % de pigment : la couleur est donc totalement blanche. De même, avec 100 % de noir, on n’a que du noir.
Si l’on met 45 % de blanc et 45 % de noir, on obtient du gris, et il reste 10 % pour la couleur. On a donc une couleur délavée dans beaucoup de gris.
Si l’on met 0 % de blanc et 0 % de noir, on a seulement de la couleur, qui est alors très vive :

Et toujours la représentation de notre orange (notez que l’angle de teinte est identique à chaque fois) :
-
hsv(30 87% 80%) -
hsl(30 77% 45%) -
hwb(30 10% 20%)
Pour conclure
Plusieurs systèmes cylindriques existent et utilisent toutes des logiques basées sur la façon psychologique et intuitive de former les couleurs. Ils n’utilisent pas de synthèse des couleurs, comme RGB ou CMY, mais une séparation claire entre une teinte donnée, puis l’intensité de cette teinte sur une échelle du blanc au noir.
HSV, HSL et HWB sont tous bijectifs sur l’espace RGB (et CMY) : ils contiennent les mêmes 16,7 millions de couleurs. D’autres formats, notamment Lab, et Luv (qui sont cartésiens, mais pas trichromiques) ont également leur penchant cylindrique : LCh(ab) et LCh(uv). Ces espaces-là sont décrits dans l’article suivant.
Les trois systèmes HSV, HSL et HWB sont très proches, et utilisent notamment le même angle (la première des trois valeurs) pour une même teinte donnée. Cela ne sera pas le cas, par exemple, du système OkLab, où il existe également un angle, mais légèrement différent de celui des systèmes HSV et ses variantes.
Comment représenter une couleur : les formats trichromiques, RGB et CMY
Couleur science par Anonyme le 03/02/2025 à 20:16:00 - Favoriser (lu/non lu)

- Comment représenter une couleur : les formats trichromiques, RGB et CMY (le présent article) ;
- Comment représenter une couleur : les formats cylindriques, HSV et HSL ;
- Comment représenter une couleur : les formats employant la luma, Y’UV et dérivés ;
- Comment représenter une couleur : les formats standards de la CIE, XYZ, Lab, Lch.
Les couleurs sont l’expression par le cerveau de l’énergie1 portée par les ondes électromagnétiques reçues par l’œil. On parle aussi de la longueur d’onde. Si les longueurs d’onde sont une réalité physique, les couleurs en revanche sont là uniquement dans notre tête.
Qui plus est, les couleurs que nous connaissons (rouge, bleu, jaune, etc.) ne sont l’expression que d’une toute petite portion de toute la gamme des longueurs d’onde possible. Les longueurs d’ondes peuvent être très longues (ondes radio, micro-ondes), ou très courtes (rayons X, rayons gamma). La plage des ondes visibles est une petite fraction de tout ce qui se trouve entre les deux.
La perception de ces ondes lumineuses est assurée par l’œil, et plus précisément par des cellules situées au fond de l’œil : les cônes et les bâtonnets. Les bâtonnets servent essentiellement pour capter les niveaux de luminosités (essentiellement quand la luminosité est faible, la nuit par exemple). La perception des couleurs est elle assurée par les cônes.
Sur un œil humain « normal », on trouve trois types de cônes, sensibles respectivement aux longueurs d’onde longues (du rouge), moyennes (du vert) et plus courtes (du bleu). Ceci est une représentation simplifiée des choses : en réalité, les cônes captent toutes les longueurs d’onde, c’est juste qu’il en capte mieux certaines (les longues, moyennes ou courtes) que le reste.
Le fait de parler des couleurs fondamentales que sont le rouge, le vert et bleu, commence ici. Il s’agit des couleurs de la lumière qui nous arrive et celles auxquelles nos cônes répondent le mieux.
Pourquoi représenter une couleur ?
Lorsque l’on parle de rouge ou de bleu, en supposant une perception des couleurs dite « normale », on se représente très bien ce que c’est. Cela suffit ainsi pour comprendre « le ciel est bleu » ou « cette fleur est rouge », et s’imaginer la scène ou l’objet de la discussion.
Maintenant, lorsque l’on commence à parler technique, informatique, couleurs commerciales (pour une marque : le « rouge Coca-Cola » par exemple), ou standardisées (le bleu du drapeau français n’est pas le bleu du drapeau luxembourgeois par exemple), il faut être un peu plus précis que simplement « rouge » ou « bleu ».
Il a donc fallu mettre au point des systèmes de représentation des couleurs. Il en existe plusieurs. Il en existe un très grand nombre, à vrai dire.
La plus simple consiste à se servir d’un nuancier : une plaquette avec des taches colorées numérotées, ou nommées. En donnant à tout le monde la même plaquette, et en référant au numéro ou au nom de la couleur, tout le monde sait de quoi on parle. C’est le but des nuanciers standardisés, par exemple du nuancier Pantone® :

Les nuanciers Pantone® sont une référence mondiale (mais pas une norme ISO). Ils sont utilisés dans beaucoup d’endroits, mais ils coûtent très cher et peuvent s’user ou s’abîmer. De plus, on ne peut pas utiliser un nuancier physique (l’objet lui-même) dans une télé, par exemple, quand il s’agit de transmettre des couleurs dans le signal de votre récepteur multimédia.
Que ce soit pour la télé couleur, ou encore pour l’encodage des couleurs dans un JPEG, dans la vidéo H264 en HD, il faut un système un peu moins matériel, et un peu plus abstrait et mathématique pour représenter une couleur. Par exemple une représentation comme rgb(255, 0, 0) pour dire « rouge ».
Cette représentation, rgb(255, 0, 0), est écrite dans la représentation RGB. Il existe plein d’autres représentations, qui ont toutes leurs spécificités et leur origine. Le présent article se focalise sur ce format-ci qui utilise RGB, ainsi que son complémentaire, le CMY. D’autres formats sont décrits dans les autres articles de cette mini-série d’articles.
Les espaces trichromatiques cartésiennes
Nos yeux, je l’ai dit plus haut, utilisent des cellules appelées cônes qui sont sensibles au rouge, vert ou bleu. Cette sensibilité n’est pas exacte, mais cette trichromie est pratique : avec seulement trois récepteurs, et selon le niveau d’excitation de chacun d’entre-eux, on peut voir des milliers de couleurs différentes, même des millions !
On peut représenter ces trois couleurs dans un espace vectoriel (un repère) muni de trois coordonnées orthonormées : chaque couleur y est représentée à l’aide d’un triplet de coordonnées — les composantes trichromatiques. Dans un tel repère, la distance à l’origine représente la luminosité de la couleur et la direction sa couleur.
Cette façon d’utiliser un espace vectoriel et des coordonnées est la raison pour laquelle on parle d’espace de couleur :

Utiliser juste trois valeurs pour représenter une couleur quelconque est quelque chose d’utilisé dans la plupart des espaces de couleurs.
La trichromie rouge-vert-bleu
Cette trichromie est utilisée depuis la photographie couleur : on utilise des filtres sensibles au rouge, au vert et au bleu, pour capter puis restituer une image en couleur. Lorsque plus tard sont apparues les systèmes d’affichage numérique, on a conservé ce système : nos écrans utilisent ainsi des sous-pixels, qui sont rouges, vert et bleus.
La couleur d’un pixel est déterminée par le niveau d’excitation de chaque sous-pixel, qui peut être plus ou moins excité. Si dans la vie de tous les jours on parlerait de pourcentage d’excitation, dans le monde numérique fait d’octets, l’échelle va de 0 à 255. La raison est que 255 c’est le nombre de valeurs qu’il est possible de stocker sur un seul octet
Prenons une couleur, par exemple une couleur appelée « Orange Vif » dans les nuanciers Afnor. Sa représentation en pourcentage de rouge, vert et bleu serait 80 % de rouge, 45 % de vert, 10 % de bleu. Sur une échelle de 0 à 255, la même couleur devient rgb(203, 115, 26), « rgb » correspondant à red-green-blue, soit rouge-vert-bleu en anglais.
Cette notation RGB, que vous connaissez peut-être, permet de choisir 256 valeurs pour chacune des trois couleurs fondamentales (255, ainsi que le 0). Au total, on a donc 256³ = 16 777 216 de couleurs (16 millions de couleurs).
Le système RGB est utilisé pour choisir des couleurs dans des pages web, mais aussi dans Paint, GIMP, Photoshop, Word.
Nos écrans et ce système RGB sont donc faits pour décrire 16 millions de couleurs.
Le format hexadécimal
On trouve aussi la version hexadécimale du RGB.
Ce système de couleur est exactement le même, c’est juste que les nombres de 0 à 255 sont représentés non plus en base 10 mais en base 16. Les nombres vont donc de 00 à FF. Notre orange-vif est noté #CB731A, où le CBhex = 203déc, 73hex = 115déc et 1Ahex = 26déc.
Le système HEX et le système RGB sont identiques : on peut convertir d’un schéma à l’autre simplement en convertissant de la base 16 à la base 10. J’explique comment convertir dans mon article : le système binaire et l’hexadécimal.
L’utilisation de l’un ou l’autre dépendra de l’implémentation ou de la préférence de l’utilisateur. Il n’y a pas différence entre les deux.
Notes supplémentaires
On peut parfois rencontrer la notation RGBa. Le « a » correspond alors au canal alpha, qui est le nom donné au canal de la transparence. Parfois, quand on fait de la retouche photo par exemple, on peut juste appliquer comme un film transparent de couleur par-dessus une partie de l’image. Dans ce cas on utilise une couleur transparente. Le « a » correspond au niveau de transparence. Il s’agit toujours seulement de RGB.
On rencontre parfois aussi le sRGB : il s’agit d’un standard utilisant le RGB. Il s’agit de définir exactement quel rouge, quel vert, et quel bleu l’on utilise et l’on doit restituer. Ces couleurs de références sont issues d’un autre standard, la CIE XYZ, que l’on verra plus tard.
Sur un écran, les couleurs sont obtenues grâces aux matériaux utilisés pour faire ces pixels : des luminophores sur les vieux écrans, ou des cristaux liquides sur les écrans LCD, ou encore de minuscules diodes électroluminescentes colorées dans les écrans OLED.
Ainsi, si deux écrans utilisent des cristaux liquides un peu différents, le RGB ne s’affichera pas de manière identique. Un correctif devra être appliqué de façon logicielle pour que le rendu des couleurs s’approche du sRGB et que l’utilisateur puisse contempler les couleurs correctes.
La trichromie cyan-magenta-jaune
Si nos écrans utilisent du rouge, vert, bleu, nos imprimantes ainsi que les peintres utilisent le cyan (le bleu primaire), le magenta (le rouge primaire) et le jaune primaire. Ceci est parce que les écrans émettent de la lumière, alors que la peinture et les encres absorbent de la lumière.
On dit que le trio rouge-vert-bleu sont les couleurs primaires de la synthèse additive (les lumières sont émises et se cumulent), l’on parle également de couleurs fondamentales. Les cyan-magenta-jaune sont les couleurs primaires de la synthèse soustractive (les longueurs d’ondes sont absorbées et se soustraient).
Le système utilisant le cyan, magenta et jaune se nomme le système CMJ en français ou CMY en anglais (Y pour yellow, jaune).
Quand on regarde le canevas de base, c’est-à-dire l’écran éteint ou la feuille blanche, on comprend que les systèmes RGB et CMY sont complémentaires. Un écran est noir, et les illuminations des pixels donnent progressivement des couleurs de plus en plus proches d’une illumination totale, c’est-à-dire d’un écran blanc. Le CMY fait l’inverse : la toile ou le papier sont blancs, renvoient toutes les couleurs, et ajouter des pigments assombrit alors le dessin. Les deux ont une logique opposée.
En quelque sorte, le CMY est le négatif du RGB (et inversement).
Si l’on revient à notre orange-vif de tout à l’heure :
- en RGB :
rgb(203, 115, 26); - en RGB% :
rgb(80%, 45%, 10%); - en CMY :
cmy(20%, 55%, 90%)
On remarque, sur ces deux dernières lignes, que pour la même couleur, on a R+C = 100 %, G+M = 100 % et B+Y = 100 %.
Mathématiquement, les deux systèmes sont complémentaires, et on peut évidemment convertir le RGB en CMY et vice-versa avec de simples soustractions. L’on représente les conversions entre espaces de couleurs sous la forme de matrices :
$$\left(\begin{smallmatrix} C \\ M \\ Y\end{smallmatrix}\right) = \left(\begin{smallmatrix} 1 \\ 1 \\ 1\end{smallmatrix}\right) - \left(\begin{smallmatrix} R \\ V \\ B\end{smallmatrix}\right)$$
La quadrichromie CMYK
Vous aurez remarqué que votre imprimante utilise des cartouches CMY, mais également une cartouche noire. L’on parle alors de quadrichromie : cyan, magenta, jaune et noir : CMJN, ou CMYK en anglais.
L’idée est de faire des économies : en effet, quand on veut faire du noir (ce qui arrive souvent en impression, par exemple pour du simple texte) avec du CMY, on doit mettre du cyan à 100 %, du magenta à 100 % et du jaune à 100 %. Autrement dit, on met trois fois plus d’encre, alors qu’on pourrait utiliser juste une encre déjà noire.
Plus généralement, quelle que soit la couleur, du noir peut être ajouté dès lors qu’un peu de noir permet de remplacer plus d’encre couleur.
Notre orange-vif devient :
- en CMYK :
cmyk(0%, 43%, 87%, 20%): Le noir à 20 % permet de réduire à zéro le cyan, et de diminuer les autres couleurs.
On le voit également très bien quand on décompose une image en ses différentes composantes :

Et l’hexachromie ?
Utiliser trois couleurs primaires (plus le noir) peut parfois produire un rendu limité. En effet, pour obtenir des tons un peu clairs, il faut que les gouttes d’encre sur le support blanc soient suffisamment petits ou espacées pour que le rendu mélangé au blanc donne une couleur claire visuellement.
Or, en photographie, pour obtenir des photos de qualité, on ne veut pas de cette granularité dans l’image, en particulier pour les régions bleues ou rouges. Ceci est particulièrement un problème quand beaucoup de photos contiennent des portions de ciel, de mer, ou de peau humaine dans ces tons-là.
Le problème est que le magenta ou le cyan seront toujours du magenta et du cyan, et ne peuvent pas être foncés ou clairs. Si le noir peut donner facilement l’illusion d’assombrir la couleur, pour l’éclaircir c’est plus délicat. Il faudrait une encre un peu moins sombre, en particulier pour le cyan et le magenta (le jaune est lui-même assez clair pour ne pas souffrir de ce problème).
C’est exactement ce que fait l’hexachromie, qui imprime avec 6 cartouches différentes dans des imprimantes spécifiques : cyan, cyan-clair, magenta, magenta-clair, jaune et noir : CcMmYK.
Ceci demande un matériel spécifique, davantage d’encre également, et est généralement utilisé par les professionnels de la photographie.
Conclusion
Pour conclure sur le format RGB et CMY, il s’agit d’un format issu de la trichromie des yeux humains, que l’on mimique pour créer nos écrans couleur, également en RGB, sur des sous-pixels, ou les systèmes d’impression, qui sont en CMY.
Ces trois canaux à chaque fois sont dosés puis additionnées afin d’obtenir la couleur souhaitée.
D’autres méthodes existent, et pour ça je vous invite à lire les autres articles de cette série sur les couleurs.
Finissons par dire tout de même que 16 millions de couleurs dans ces deux espaces peuvent sembler beaucoup, mais ça ne représente pas toute la gamme (ou gamut) des couleurs que l’œil est capable de capter. Certaines couleurs ne sont pas affichables par nos écrans en sRGB.
La norme sRGB ayant plus de 50 ans, et la technologie ayant évoluée depuis, certains écrans peuvent désormais afficher des couleurs au-delà de sRGB, donc des couleurs qu’il est impossible à représenter en RGB (par exemple comme rgb(320, −110, −10), qui n’a aucun sens en RGB, mais qui peuvent exister dans d’autres espaces, comme la CIE XYZ, le P3 ou le OkLab. Le RGB nous fait ainsi louper des couleurs, et de nouveaux standards de couleurs sont à l’étude pour remplacer le RGB petit à petit, en tout cas pour les écrans compatibles.
Notes
[1] : il est plus rigoureux de parler de l’énergie (ou de fréquence temporelle) d’un rayon lumineux, que de parler de longueur d’onde. La longueur d’onde dépend en effet du milieu traversé : ainsi, dans l’air, le « rouge » correspond à 800 nm, alors que dans l’eau, le même rayon lumineux aura une longueur d’onde de 600 nm. Le rayon, s’il ressort de l’eau, reprendra ses 800 nm. La longueur d’onde aura donc changé sur son trajet, mais son énergie est restée la même.
Si l’on pose que le milieu considéré est l’air, on peut parler de longueur d’onde comme d’énergie. C’est ce que je fais dans toute la suite de l’article.
Comment fonctionnent les comprimés effervescents ?
Couleur science par Anonyme le 02/01/2025 à 04:10:00 - Favoriser (lu/non lu)

Un comprimé que l’on met dans l’eau et qui fait des bulles lorsqu’il se dissout : comment ça marche ?
On connaît les comprimés effervescents essentiellement pour les médicaments, mais ils existent aussi les comprimés de vitamines, les nettoyants pour dentiers ou encore pour les détergents.
Leur but, outre la praticité, est d’assurer une dissolution rapide et totale du principe actif qu’il contient. La fonction d’effervescence est, en principe mais pas forcément, assuré par des excipients. En l’occurrence, les excipients utilisés dans la plupart des médicaments en comprimés effervescents sont du bicarbonate de soude et de l’acide citrique (ou de l’acide tartrique).
Peut-être avez-vous déjà essayé de mélanger du vinaigre avec du bicarbonate de soude : cela fait des bulles. Il s’agit d’un dégagement de dioxyde de carbone, le CO2 gazeux, qui est un des produits de la réaction entre les deux composés : le bicarbonate de soude se décompose en dioxyde de carbone et en eau en présence de tout acide en phase aqueuse. L’un des acides que l’on peut utiliser est l’acide citrique.
J’ai bien dit « en phase aqueuse », car sous sa forme solide, le bicarbonate de soude et l’acide citrique ne réagissent pas : ils peuvent donc être stockés et compactés ensembles sous la forme d’une tablette : le comprimé.
Dès que l’on place le comprimé dans l’eau, les deux composés se dissolvent et réagissent ensemble. Cette réaction permet une dissolution totale et rapide du comprimé et de ses principes actifs ajoutés dedans.
L’effet effervescent assuré par les bulles produit de plus des mouvements de convection dans le verre d’eau, ce qui assure une bonne homogénéisation (en plus de jouer un rôle de placébo important : « si ça fait des bulles, c’est que ça agit, donc ça doit être efficace ! »).
L’Équation du Temps
Couleur science par Anonyme le 05/12/2024 à 04:28:00 - Favoriser (lu/non lu)

Le temps est quelque chose de mystérieux, presque indéfinissable. Pourtant, parmi tout ce que l’on peut trouver en sciences, on a un outil qui se nomme l’Équation du Temps.
Alors non, il ne s’agit pas une équation qui donnerait l’heure absolue de l’univers, où je ne sais quoi de mystique, mais cela n’enlève rien au fait qu’il y a des choses très intéressantes à dire dessus.
Tout comme il ’existe l’équation des télégraphistes qui est (ou était) utile, on s’en serait douté, aux télégraphistes et concernant la transmission du signal à travers un conducteur électrique de grande longueur ; l’équation du temps aurait pu s’appeler « l’équation des horlogers », car elle constitue un outil pour mesurer l’écart entre les horloges et l’heure solaire vraie.
En effet, il existe un décalage entre l’heure solaire réelle et l’heure sur votre montre. Ce décalage varie au cours de l’année, tantôt en positif, tantôt en négatif. Moyennée sur une année, le décalage est nul (par définition de l’heure), il n’y a donc pas besoin d’ajuster sa montre chaque année, mais le décalage existe pour un jour donné de l’année. La position exacte du Soleil dans le ciel ne suit donc pas votre montre : le moment où le Soleil est au plus haut ne correspond donc pas toujours au « midi » de la montre (et ça, sans même parler des fuseaux horaires ou de l’heure d’été).
Lorsqu’on lisait l’heure sur un cadran solaire, cela posait problème : une même position de l’ombre pouvait signifier des heures civiles différentes en fonction du jour de l’année ! Pour corriger cette erreur, les cadrans solaires étaient accompagnés de tables donnant la correction à appliquer à l’heure lue sur le cadran (l’heure solaire, donc) pour obtenir l’heure civile.
L’équation du temps condense ces valeurs tabulées en une formule mathématique plus ou moins simple.
Aujourd’hui, nous n’utilisons plus de cadrans solaires. En revanche, on utilise de plus en plus des panneaux solaires, et ces derniers sont plus efficaces lorsqu’ils font face au Soleil. Certains panneaux solaires sont fixés sur un axe pivotant qui suivent la position du Soleil dans le ciel, comme un tournesol. Pour ces systèmes, connaître la position du Soleil devient critique, et l’équation du temps (re)devient quelque chose d’important. Ceci est encore plus vrai pour les centrales solaires à concentration (ceux avec un champ de miroirs et une tour au milieu), où les miroirs doivent suivre le Soleil avec une très grande précision, et où un décalage n’est pas admissible.
Heure solaire et heure civile ? Un décalage ?
Depuis que nous mesurons l’heure et les jours, probablement depuis l’Égypte antique, à qui l’on doit d’ailleurs notre découpage de la journée en 24 heures, on a toujours considéré que tous les jours avaient la même durée.
Cette durée a servi de base pour le découpage en 24 heures. Un jour « civil » vaut donc précisément 24 heures.
En réalité, c’est plus compliqué que cela : les jours n’ont pas tous la même durée ! Pour expliquer pourquoi, rappelons tout d’abord ce qu’est une journée.
Jour sidéral et jour solaire
Une journée, telle qu’on le définit habituellement, c’est la durée d’une rotation de la Terre sur elle-même : quand la Terre effectue un tour complet sur elle-même alors on parle d’un jour.
Un tour complet, c’est 360° : c’est cela que l’on appelle une journée. Plus précisément, c’est ce qu’on appelle une journée sidérale. En effet, ces 360° sont mesurés par rapport à un référentiel considéré comme fixe, à savoir des étoiles suffisamment lointaines pour que notre déplacement sur l’orbite autour du Soleil n’en modifie pas l’emplacement dans le ciel au fil des jours.
Après un jour sidéral, donc, les mêmes étoiles lointaines ont exactement la même position dans le ciel.
Ou, pour le dire autrement : la durée séparant deux moments consécutifs pour lesquels les mêmes étoiles sont à la même place dans le ciel, est appelée jour sidéral.
Maintenant, le Soleil.
Lui, il n’aura pas la même position dans le ciel : il n’est pas assez distant, et la Terre orbite autour. Quand on se déplace par rapport à lui, sa position apparente change.
Une année compte 365,2425 jours. Chaque jour qui passe, la Terre effectue 1/365,2425ᵉ de révolution complète. Puisqu’une une révolution complète correspond aux 360° de l’orbite, le déplacement quotidien est de 360°/365,2425 j, ce qui correspond à 0,985°, soit environ 1° par jour.
La conséquence directe de ceci est que la position du Soleil dans le ciel change de ~1° chaque jour sidéral de l’année.

Pour que le Soleil occupe la même position dans le ciel, il faut donc que la Terre effectue non pas 360°, mais 361° sur son axe. Ceci prend environ 4 minutes supplémentaires.
La durée qui sépare deux moments consécutifs où le Soleil reprend sa place dans le ciel, est appelé très logiquement le jour solaire.
Or, lorsque nous avons défini l’heure comme étant la 24ᵉ fraction de la journée, on a regardé le Soleil, pas les étoiles lointaines. C’est le jour solaire qui permet de définir le jour civil.
Un jour solaire mesure donc 24 h par définition. Le jour sidéral, lui, dure un peu moins, à savoir 23 h 56 min 4 s (environ 4 minutes en moins).
Le jour solaire est une moyenne
Quand je dis que le jour solaire dure 24 heures par définition, c’est faux. Il s’agit en vérité d’une moyenne sur une année : c’est cette moyenne sur l’année qui dure par définition 24 heures. Les journées individuelles varient un peu, notamment à cause de la forme de l’orbite terrestre autour du Soleil et de l’inclinaison de l’axe de la Terre. Voyons tout ça.
Influence de la forme de l’orbite terrestre : l’équation du centre
On a donc vu que c’est le déplacement de la Terre sur son orbite qui produit la différence entre le jour sidéral et le jour solaire d’environ 4 minutes. Or, l’orbite de la Terre n’est pas un cercle : c’est une ellipse, qui plus est une ellipse excentrée très légèrement. Certaines parties de l’orbite sont plus proches du Soleil que d’autres.
À cause de cette forme irrégulière, la vitesse de déplacement de la Terre autour du Soleil est également irrégulière : la Terre se déplace plus vite lorsqu’elle est proche du Soleil et moins vite lorsqu’elle en est loin (c’est la loi de Kepler). Le moment où la Terre est au plus proche du Soleil se nomme le périhélie, qui a lieu chaque année autour du 3 janvier, et le moment où elle en est le plus éloigné est l’aphélie, qui a lieu six mois plus tard, vers le 3 ou 4 juillet :

Ces ~1° supplémentaires, ou ces 4 minutes de décalage sont donc une moyenne également. Il faut donc, pour la Terre, parfois un peu plus, parfois un peu moins de temps pour rattraper l’heure solaire.
Numériquement, l’amplitude de ces variations durant l’année se situe autour de ±7,6 minutes ! C’est loin d’être anodin.
Nos horloges calquées sur la moyenne de 24 heures exactement sont donc tantôt en avance, tantôt en retard sur le Soleil. Ce décalage est nul lors de l’aphélie et de la périhélie.
Ce décalage dû à la forme de l’orbite terrestre est appelé équation du centre, et il peut être représenté sous la forme d’une sinusoïde :

Influence de l’inclinaison de l’orbite terrestre : la réduction à l’équateur
En plus de l’irrégularité de la vitesse de la Terre sur son orbite, l’inclinaison de l’axe de rotation de la Terre provoque également un décalage. La Terre est incliné d’environ 23,44° par rapport au plan de son orbite, ou plan de l’écliptique.
Là aussi, cela influence la position apparente du Soleil dans le ciel : le Soleil progresse chaque jour de ~1° sur le plan de l’écliptique. Or, la rotation supplémentaire que la Terre fait pour se remettre face au Soleil est fait dans le plan de l’équateur !
L’expression dans le référentiel de l’équateur de ce décalage dans le référentiel de l’écliptique implique un second correctif.
Ce décalage-ci compte pour environ ±9,8 minutes au cours d’une année, et il s’annule en particulier lorsque le plan de l’équateur traverse l’écliptique, c’est-à-dire aux équinoxes, ainsi que lors des solstices.
Ce décalage est appelé réduction à l’Équateur, et il s’agit à nouveau d’une sinusoïde. Celle-ci possède deux périodes au cours d’une année :

Combinaison des deux phénomènes : équation du temps
Les deux phénomènes vus précédemment ne sont pas en phases : étant d’origines différentes, elles n’ont pas à l’être. Toutefois, c’est bien leur action combinée — leur somme — qui constitue le décalage global entre l’heure solaire vraie (position du Soleil) et l’heure solaire moyenne (heure civile) :

L’ordonnée de cette courbe montre, pour une journée donnée de l’année, ce décalage en minutes. Ce décalage, cette courbe, est ce que l’on appelle l’équation du temps.
Une dernière chose : si l’on dessine chaque jour la position la plus haute du Soleil à la même heure (midi, heure solaire moyenne), on obtient une figure caractéristique en forme de « 8 » appelée analemme. C’est ce que l’on voit dans l’image d’en-tête.
Elle montre de façon visuelle la position du Soleil à midi — midi civil — pour chaque jour de l’année, et l’on constate bien que le Soleil n’est pas toujours à la même place, malgré le fait qu’il soit bien midi à notre montre pour chaque photo.
Une autre façon d’obtenir ce dessin, c’est au sol en traçant l’ombre de la pointe d’un poteau ou d’un lampadaire, par exemple, chaque jour de l’année, à midi (heure civile, hors heure d’été). À la fin de l’année, on observera une analemme au sol.
Plusieurs niveaux de précision
L’équation du temps, ici, ne tient compte que des paramètres orbitaux de la Terre : excentricité et ellipticité de l’orbite, et inclinaison de son axe de rotation. Ce sont là les deux paramètres les plus influents.
Ces paramètres sont dus à des causes différentes et arbitraires, mais les décalages qu’elles produisent au cours d’une année sont, en première approximation, identiques d’une année sur l’autre. Une équation assez simple constituée de la somme des deux sinusoïdes fonctions de d, peut donc être construite, où d est le jour de l’année (entre 1 et 365, ou 366 ; et le résultat Δt est en minutes décimales) :
$$\Delta t = -7,655 ⋅ \sin(d) + 9,873 ⋅ \sin(2d + 3,588)$$
Cette équation empirique est valable tous les ans, à notre époque (−1000/+1000 ans), et donne une estimation du décalage entre l’heure solaire et l’heure civile avec une justesse d’environ 2 minutes (soit 0,5° dans la position du Soleil dans le ciel). Il s’agit d’un calcul approché qui suffit amplement pour l’application des panneaux solaires photovoltaïques orientables mentionné dans l’introduction.
Dans d’autres cas, on a besoin d’une précision plus importante, et les calculs deviennent plus complexes. Là, sont alors pris en compte plus de paramètres.
$$\begin{aligned}T &= \frac{jd-2415020.0}{36525} \\ \epsilon &= 23.452294 - 0.0130125T - 0.00000164T^2 + 0.000000503T^3 \\ \nu &= \tan^2(\epsilon/2) \\ L &= 279.69668 + 36000.76892T + 0.0003025T^2 \\ e &= 0.01675104 - 0.0000418T - 0.000000126T^2 \\ M &= 358.47583 + 35999.04975T - 0.000150T^2 - 0.0000033T^3 \\ \Delta t &= \nu\sin(2L) - 2e\sin(M) + 4e\nu\sin(M)\cos(2L) - \frac{1}{2}\nu^2\sin(4L) - \frac{5}{4}e^2\sin(2M) \\ \end{aligned}$$
Où :
- T : la date (exprimée en siècles de calendrier julien) ;
- ε (epsilon) : obliquité (inclinaison) de l’axe de rotation ;
- ν (nu) : l’anomalie vraie ;
- L : la longitude moyenne du Soleil ;
- e : excentricité de l’orbite ;
- M : l’anomalie moyenne.
Et :
- Δt : l’équation du temps.
Les deux paramètres que sont l’obliquité et l’excentricité sont variables d’année en année et ajustés avec des constantes, sont ici recalculées. En effet, ces paramètres varient très légèrement avec le temps et cette seconde approximation tient compte de ça. Cette nouvelle précision donne une justesse de quelques secondes sur l’équation du temps, et cette dernière conserve cette précision sur une plage de temps d’environ 6 000 ans.
Enfin, pour un calcul encore plus précis, on doit prendre en compte la variation de ces constantes elles-mêmes ! Là aussi avec des fonctions empiriques encore plus étendues. Tous ces paramètres évoluent en effet en fonction d’un grand nombre d’influences extérieures :
- l’influence des autres astres (planètes, lunes…), qui modifient très légèrement l’orbite et l’inclinaison de la Terre ;
- l’influence des forces de marée (du Soleil et de la Lune), qui tendent à ralentir la rotation terrestre au fil des éons ;
- la précession du périastre (l’orientation de l’éclipse de notre orbite, qui tourne également) ;
- la nutation (rotation de la direction de l’inclinaison de l’axe de la Terre).
- …
Ces phénomènes-là sont beaucoup plus légers que ceux intervenant dans l’équation du temps simplifiée ou semi-simplifiée, mais leur prise en compte devient nécessaire lorsqu’on requiert une justesse très importante, de l’ordre de 0,01 seconde, et valables sur des dizaines de milliers d’années.
Ce que l’on considère comme des constantes en première approximation dans la version simplifiée est donc peu à peu paramétré en fonction du temps. Les constantes deviennent donc variables, et rendent donc plus précises les calculs. Ce genre de méthode, où la précision des calculs est plus ou moins complexe est souvent utilisé en astronomie selon le niveau de précision requis (et selon le niveau de puissance de calcul disponible, bien que ceci ne soit plus vraiment un souci aujourd’hui).
Et l’équation des équinoxes ?
L’équation du temps permet d’estimer le décalage du Soleil à cause de la variation d’une journée solaire durant l’année. Le jour sidéral, qui prend les étoiles distantes pour référence est bien plus régulier.
Bien plus, mais pas parfaitement.
Là aussi, divers paramètres légers peuvent influencer la durée d’un jour sidéral. Si l’on utilise les calculs expliqués juste au-dessus avec les influences des planètes et de la précession des équinoxes, alors on se rend compte que les jours sidéraux varient également. On se retrouve là également avec un temps sidéral moyen (moyenné sur une année) et un temps sidéral vrai (ou apparent).
Le décalage entre le temps sidéral moyen et le temps sidéral vrai est appelé équation des équinoxes.
Ici aussi, pour avoir quelque chose de très précis, les calculs deviennent fastidieux. Il faut savoir que les positions des autres planètes ont une influence sur notre orbite, mais l’inverse est vrai également, et les planètes entre elles s’influencent également. Dans l’ensemble, cela fait beaucoup d’ajustements.
Ceci dit, la mécanique céleste est complexe, mais régulière. Les calculs sont donc compliqués, mais sont essentiellement constitués de fonctions trigonométriques « simples ». Au final, on peut obtenir des valeurs extrêmement précises, de l’ordre du centième de milliardième de degré angulaire sur la position d’une étoile dans le ciel, au prix de nombreux calculs.
Ressources
Pages web en ligne :
- Solar time - Wikipedia ;
- Précession du périastre — Wikipédia ;
- Equation Of Time - Simplified — celestialprogramming.com ;
- Apparent solar time (True solar time)/Equation of time ;
- Online calculator: Equation of time ;
- The Sun's Position | PVEducation ;
- Sidereal Time Calculator For Any Date, Time and Longitude ;
Ouvrages papier :
- Astronomical Algorithms, Secondth Edition, Jean Meeus, 1998 (ISBN : 978-0943396613 ; lien Amazon)
- Textbook On Spherical Astronomy, Sixth Edition, W. M. Smart, 1977 (ISBN : 978-0521215169 ; lien Amazon)
Et mon outil en ligne qui affiche l’équation du temps à un moment donné :
Ah, la science… (16)
Couleur science par Anonyme le 07/11/2024 à 17:49:00 - Favoriser (lu/non lu)

Un petit article avec des chiffres intéressants, ça faisait longtemps ! Voici donc le 16ᵉ épisode de la série devenue récurrente (les autres épisodes sont en bas de l’article).
50 à 60 km par an
C’est le déplacement qu’effectue le pôle Nord magnétique.
Le champ magnétique terrestre prend sa source avec des courants électriques dans le noyau en rotation de notre planète. Ce noyau tourne sur un axe qui ne coïncide pas totalement avec l’axe de rotation de la Terre. Il en résulte que le pôle Nord magnétique (et son pôle Sud) ne coïncident pas avec le pôle Nord géographique (et le pôle Sud géographique).
De plus, les fluctuations électromagnétiques au fil du temps dans le noyau font que le pôle Nord magnétique se déplace constamment : de l’ordre de 50 à 60 km chaque année.
Le pôle Nord magnétique, qui était au Canada avant l’an 2000, est désormais passé à côté du pôle Nord géographique, et glisse petit à petit vers la Sibérie.
0,5 %
C’est ce que l’on pèse de moins sur la balance en se trouvant à l’équateur, par rapport aux pôles (pôles géographiques). Quelqu’un qui pèse 100 kg aux pôles pèsera environ 99,5 kg sur l’équateur. Du moins, c’est ce que qu’affichera la balance.
En effet, le pèse personne nous affiche la force avec laquelle nous sommes retenus les pieds sur Terre. Il y a deux facteurs qui influent sur ça.
Premièrement, notre masse corporelle est fixe mais notre poids résulte de la force de gravité avec laquelle la Terre nous attire. Cette force dépend de la distance au centre de la Terre. Or, la Terre est aplatie aux pôles et bombée à l’équateur : on est donc plus proche du centre de la Terre quand on est situé sur un pôle. Il en résulte que l’on pèse un peu plus aux pôles, et un peu moins sur l’équateur.
Secondement, il faut prendre en compte l’effet centrifuge : la rotation de la Terre se fait suivant l’équateur. Sur l’équateur, on se déplace à environ 1 660 km/h à cause de la rotation terrestre. Ceci produit un effet centrifuge qui nous soulève un tant soit peu du sol. Cet effet diminue au fur et à mesure que l’on s’approche des pôles.
Sur les 0,5 % que nous pesons en moins, les deux tiers sont dus à l’effet centrifuge, et le tiers restant provient du rapprochement au centre de la Terre (source).
260 tonnes par jour
Il s’agit de la masse de gaz atmosphériques que nous perdons chaque jour dans l’espace. On parle d’échappement atmosphérique.
Dans l’air, les molécules se déplacent constamment et s’entrechoquent. La vitesse des atomes dépend de la température, mais la moyenne est de l’ordre de 1 800 km/h à température ambiante. Il s’agit d’une moyenne, donc certaines vont plus vite, même beaucoup plus vite que ça. Cette vitesse peut être acquise lors de chocs avec de particules cosmiques, des réactions chimiques, ou simplement de la distribution ordinaire des vitesses.
En particulier dans la haute atmosphère, certaines peuvent avoir des vitesses dépassant la vitesse de libération gravitationnelle : la vitesse au-delà de laquelle un corps ne retombe jamais sur son astre. Ceci est particulièrement vrai pour les gaz légers comme l’hydrogène ou l’hélium. À cet endroit, les chocs sont également plus rares du fait de la raréfaction des molécules et le libre parcourt moyen (déplacement avant un autre choc) peut être infini : une particule n’en heurte jamais aucune autre. Si toutes ces conditions sont réunies, un atome peut donc partir dans l’espace et être définitivement perdue pour notre atmosphère.
Dans l’ensemble, on estime à 260 tonnes de gaz qui s’échappe ainsi de notre planète. Chaque jour.
Bien sûr, notre planète capte également des débris et des poussières interplanétaires, et de l’ordre de 110 tonnes par jour. Cela ne compense donc pas l’échappement atmosphérique, ni quantitativement (on perd plus que l’on gagne) ni qualitativement : on perd des gaz et on gagne de la poussière solide.
Ce phénomène est d’ailleurs un défi concernant une éventuellement terraformation de la planète Mars : Mars est moins massif que la Terre, donc l’échappement est favorable, la vitesse de libération étant plus facile à atteindre, et l’absence de bouclier magnétique favorise également l’interaction avec les vents solaires et particules cosmiques.
Ah, la science : (épisode 15 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1.)
Le calendrier républicain français
Couleur science par Anonyme le 03/10/2024 à 05:08:00 - Favoriser (lu/non lu)

Cet article a été publié le duodi 12 vendémiaire, de l’an CCXXXIII, jour de l’immortelle.
Perplexe ? Il s’agit de la date de publication de l’article (jeudi 3 octobre 2024) exprimé dans un autre calendrier, celui de l’ère républicaine française et mis en place peu après la révolution française, en 1792 (et officiellement adoptée en 1793).
Lors de révolution française en 1789, les sans-culottes ne se sont pas contenté de la décapitation du Roi et du changement de système politique. En plus de mettre en place un système républicain et de déclarer les Droits de l’Homme et du Citoyen, ils ont voulu marquer le coup en faisant table rase de tout le reste également.
Une remise à zéro des unités de mesure
Sur le plan technique et scientifique, on eut droit à une remise à zéro des unités de mesure. Les unités courantes (de poids, de longueur), à l’époque, n’était pas uniformes : chaque région, chaque ville, chaque commerçant parfois, avait les siennes, ce qui posait souvent problème. Si la nécessité d’une uniformisation avait été reconnue par Louis XVI, ce sont les révolutionnaires entamèrent les travaux de ce qui deviendra plus tard le système métrique en France, et, aujourd’hui, le Système International d’Unités dans le monde.
Oui, le Système International est français !
Plus radical : les révolutionnaires ont même jeté le calendrier et l’horloge à la poubelle. Jugé pas assez métrique, pas assez décimal, et trop royaliste et religieux, il fallait le réviser. Un nouveau calendrier fut donc mis au point : le calendrier républicain.
La création d’un nouveau calendrier
Ce calendrier français est centré sur la France. Les décrets de l’époque parlent même de « l’Ère des Français ». Les années sont remises à zéro, et la première, débutant le 22 septembre 1792, est nommée « an I », que l’on retrouve alors officiellement sur les documents et les monnaies d’époque, entre autres.
Le but ? En plus de couper avec le passé, il fallait simplifier tout ça. Les mois de 30, 31, 28 ou 29 jours, commençant à un moment de l’année arbitraire de l’année solaire, sont remplacés par un calendrier où chaque mois dure 30 jours et l’année commençait à une date ayant une signification révolutionnaire (celle de la Révolution française). Elle débute le lendemain de la proclamation de l’abolition de la Monarchie, qui par un hasard, tomba également sur une date ayant une signification astronomique, à savoir l’équinoxe d’automne.
Ce changement fut décidé par le Décret de la Convention nationale portant sur la création du calendrier républicain, en ces termes :
Chaque année commence à minuit, avec le jour où tombe l’équinoxe vrai d’automne pour l’observatoire de Paris.
[…]
L’année est divisée en douze mois égaux, de trente jours chacun : après les douze mois suivent cinq jours pour compléter l’année ordinaire ; ces 5 jours n’appartiennent à aucun mois. […] Les cinq derniers jours s’appellent les Sansculotides.
[…]
Chaque mois est divisé en trois parties égales, de dix jours chacune, qui sont appelées décades.
[…]
L’année ordinaire reçoit un jour de plus, selon que la position de l’équinoxe le comporte, afin de maintenir la coïncidence de l’année civile avec les mouvements célestes. Ce jour, appelé jour de la Révolution, est placé à la fin de l’année et forme le sixième des Sansculotides.
La période de quatre ans, au bout de laquelle cette addition d’un jour est ordinairement nécessaire, est appelée la Franciade, en mémoire de la révolution qui, après quatre ans d’efforts, a conduit la France au gouvernement républicain. La quatrième année de la Franciade est appelée Sextile.
[…]
Le décret complet est là, ou là, je n’ai pas tout mis ici.
On y trouve tout ce qu’il faut.
Architecture d’une année
Si l’on résume les points du décret ci-dessus :
- L’année compte 12 mois, tous de 30 jours ;
- Chaque mois est divisé en 3×10 jours ;
- 5 (ou 6) jours sont ajoutés à la fin pour atteindre les 365 (ou 366) jours de l’année solaire.
Sur un calendrier avec des mois réguliers, il y a obligatoirement des jours restants, car l’année solaire n’est pas un multiple entier du nombre de jours dans un mois. On retrouvait ces jours restants également dans le calendrier de l’Égypte antique, également régulier. De tels jours sont qualifiés d’épagomènes, mais dans le calendrier républicain, on parle de sansculotides.
L’année solaire n’est pas non plus un multiple entier du nombre de jours. Il reste donc une fraction de journée chaque année et qui doit être rattrapée de temps en temps : on retrouve donc le principe de l’année bissextile. Tous les 4 ans environ, on ajoute une journée grâce aux heures accumulées sur les trois années précédentes. Une telle année avec 6 sansculotides est nommé année sextile, et ce jour supplémentaire est nommé jour de la Révolution.
Début de l’année
Chaque année commence à minuit, avec le jour où tombe l’équinoxe vrai d’automne pour l’observatoire de Paris.
L’équinoxe, j’en parle dans mon article dédié — Équinoxe ou Solstice — correspond au moment exact où le zénith traverse l’équateur. Ce dernier se déplace chaque jour, et oscille d’un hémisphère à l’autre deux fois par an. Lorsque cela se produit, c’est l’équinoxe. Il s’agit d’un instant précis (pas d’une journée entière).
Il est ainsi précisé que cet instant précis est mesuré par l’Observatoire de Paris, et donc l’heure de Paris (et non Greenwich, avec lequel il existe un décalage pouvant suffire pour changer la date de l’équinoxe). Dans ce calendrier, l’heure de référence est celle de Paris.
Les saisons
La logique de ce calendrier ne s’arrête pas avec des mois de 30 jours. Elle va plus loin.
Telle que ce calendrier fut défini, chaque groupe de trois mois correspond aux saisons civiles : l’automne, l’hiver, le printemps, l’été (plus les 5 ou 6 jours des sansculotides).
Ces mois ont été nommés d’après la réalité quotidienne de ces mois en France. En effet, il fallait aider le peuple dans sa vie quotidienne : le mois à cheval sur juillet et août était ainsi appelé « thermidor », pour rappeler que c’est le mois des chaleurs estivales. Le mois à cheval sur décembre et janvier est lui nommé « nivôse », rappelant la neige.
La liste complète :
| Saison | Mois | Dates (approx.) | Période… |
|---|---|---|---|
| Automne | Vendémiaire | 23 Sept.-22 Oct. | … des vendanges |
| Brumaire | 23 Oct.-21 Nov. | … des brumes et brouillards | |
| Frimaire | 22 Nov.-21 Déc. | … du froid | |
| Hiver | Nivôse | 22 Déc.-20 Janv. | … de la neige |
| Pluviôse | 21 Janv.-19 Fév. | … de la pluie | |
| Ventôse | 20 Fév.-21 Mars | … du vent | |
| Printemps | Germinal | 22 Mars-20 Avr. | … de la germination des plantes |
| Floréal | 21 Avr.-20 Mai | … de la floraison | |
| Prairial | 21 Mai-19 Juin | … des récoltes des prairies | |
| Été | Messidor | 20 Juin-19 Juil. | … des moissons |
| Thermidor | 20 Juil.-18 Août | … des chaleurs | |
| Fructidor | 19 Août-17 Sept. | … de la récolte des fruits |
Comme je l’ai dit, tout ça est centré sur la France. Les mois neigeux ou pluvieux ne correspondraient à rien au Moyen-Orient par exemple, et les mois des moissons n’aurait sûrement aucun sens au Groenland non plus. Toutefois, ces noms, au contraire des mois du calendrier grégorien, sont issues de la nature ou de l’activité humaine, pas de la religion, de la mythologie ou de la politique.
Les mois correspondant à une même saison sont suffixés de la même façon :
- -aire pour l’automne
- -ôse pour l’hiver
- -al pour le printemps
- -idor pour l’été
… que l’on peut retenir avec le moyen mnémotechnique « aire-ôse-al-or », soit « Et Rose, alors ? ».
Les décades (ou nouvelles « semaines »)
La notion de semaines de 7 jours est remplacée par celle des décades de 10 jours.
Le nom des jours est également modifié et leur nombre ajusté. Chaque jour d’une décade porte ainsi les noms assez évocateurs :
| jour de la décade | Nom |
|---|---|
| 1ᵉʳ | Primidi |
| 2ᵉ | Duodi |
| 3ᵉ | Tridi |
| 4ᵉ | Quartidi |
| 5ᵉ | Quintidi |
| 6ᵉ | Sextidi |
| 7ᵉ | Septidi |
| 8ᵉ | Octidi |
| 9ᵉ | Nonidi |
| 10ᵉ | Décadi |
Là également, ces noms numéraux tranchent avec les noms issus des divinités romaines et des astres des jours de la semaine du calendrier Grégorien
Les fêtes de chaque jour
Sur les calendriers français actuel, nous constatons la présence de prénoms, les « saints ». Il s’agit là d’un héritage catholique (les pays protestants ne le font pas). Ces prénoms correspondent à des saints catholiques, qui sont fêtés un jour de l’année.
Ceci est une autre chose que le calendrier républicain a transformé à sa manière pour être plus laïc et pratique. Exit les saints : chaque jour se voit attribuer une plante ou un animal représenté en France, ou encore des inventions ou des productions françaises.
Ces attributions étaient prévues pour changer d’une année sur l’autre, mais finalement la liste fut fixée et appliquée tous les ans. Ainsi, pour le mois de fructidor (à cheval sur nos mois d’août et septembre), on aura :
| 1 | Jour de la Prune | 16 | Jour du Citron |
| 2 | Jour du Millet | 17 | Jour de la Cardère |
| 3 | Jour du Lycoperdon | 18 | Jour du Nerprun |
| 4 | Jour de l’Escourgeon | 19 | Jour du Tagette |
| 5 | Jour du Saumon | 20 | Jour de la Hotte |
| 6 | Jour de la Tubéreuse | 21 | Jour de l’Églantier |
| 7 | Jour du Sucrion | 22 | Jour de la Noisette |
| 8 | Jour de l’Apocyn | 23 | Jour du Houblon |
| 9 | Jour de la Réglisse | 24 | Jour du Sorgho |
| 10 | Jour de l’Échelle | 25 | Jour de l’Écrevisse |
| 11 | Jour de la Pastèque | 26 | Jour de la Bigarade |
| 12 | Jour du Fenouil | 27 | Jour de la Verge d’or |
| 13 | Jour de l’Épine-vinette | 28 | Jour du Maïs |
| 14 | Jour de la Noix | 29 | Jour du Marron |
| 15 | Jour de la Truite | 30 | Jour du Panier |
La praticité des décades et des mois réguliers commence à se faire voir : les jours 5, 15, et 25 fêtent des animaux. Les jours 10, 20, 30, des outils et instruments ruraux. Il en sera de même pour les autres mois.
Les 24 autres jours du mois fêtent des plantes sauvages ou agricoles (fleurs, fruits, légumes, arbres…), mais aussi des productions minérales (granit, sel, cuivre, étain…) ou agricoles (fumier, tourbe…), notamment pour le mois de nivôse, durant lequel la neige recouvrant les plantes, il fallut trouver autre chose.
De plus, les plantes ou outils fêtés au cours d’un mois sont censés référer le plus possible au mois. Ainsi, durant le mois des vendanges, vendémiaire, on a les outils de la cuve, du pressoir et du tonneau, et le premier jour est celui du raisin.
Pour prairial, le mois de la moisson des prairies, l’on trouve la faux, la fourche et le chariot et un bon nombre de plantes cultivées (seigle, avoine, blé…). Durant fructidor, ce sont l’échelle, la hotte et le panier, essentiels à la cueillette des fruits qui sont mis en avant.
Et l’horloge ?
L’heure est également redéfinie. Exit les journées de 24 heures de 60 minutes de 60 secondes. Désormais (toujours du même décret) :
Le jour, de minuit à minuit, est divisé en 10 parties ou heures, chaque partie en dix autres ; ainsi de suite jusqu’à la plus petite portion commensurable de la durée. La 100ᵉ partie de l’heure est appelée minute décimale ; la 100ᵉ partie de la minute est appelée seconde décimale.
On trouve donc des horloges d’époque graduées pour correspondre à ce décret.
Pourquoi ce calendrier n’est pas resté
Il n’aura échappé à personne qu’aujourd’hui nous n’utilisons plus un tel calendrier. Nous utilisons le calendrier Grégorien, notre calendrier « normal ».
En effet, le calendrier Républicain n’a pas su s’imposer dans la durée. Ni en France, et encore moins dans le monde. Il n’a en vérité duré que 12 ans en France. C’est Napoléon qui l’abbrogea en 1806, pour revenir au calendrier Grégorien.
Faire appliquer un changement de calendrier est difficile sur le plan logistique. Non seulement, ce n’est pas pratique de remettre en cause le calendrier précédent (Grégorien, basé sur le Julien) utilisé depuis l’époque romaine dans tout l’occident et même ailleurs, mais aussi sur le plan politique : la révolution française est ce qu’elle est : française, pas mondiale ; et les autres pays n’en ont que faire de ce qu’ils voyaient probablement comme une excentricité franco-française.
Aussi, l’équinoxe, qui marque le début d’une année, varie d’année en année, et le fait de démarrer l’année selon une date variable irrégulière n’était pas pratique. Tous les calendriers subissent le même soucis, y compris le calendrier Grégorien, mais ce dernier règle cela avec des années bissextiles régulièrement espacées de 4 ans (avec des correctifs tous les 100 et tous les 400 ans, donc là également bien régulières).
D’autres critiques furent également faites, comme la durée des décades : 10 jours avec seulement un jour reposé (le décadi) était difficile, ou encore une non représentation de la réalité très catholique de la France à cette époque : les avis sur la laïcité n’étaient pas partagés par tout le monde.
Dans l’ensemble, ce calendrier fut donc aboli assez vite, malgré des avantages de régularité, de laïcité pourtant évidente pour qui y accorde de l’importance.
Et aujourd’hui ?
Peut-on connaître quel jour serait aujourd’hui dans un tel calendrier ? Oui !

Les règles pour établir le commencement de l’année sont écrits. Il n’est pas impossible de relancer un tel calendrier pour une année quelconque, en dehors de son époque d’utilisation. Il « suffit » de savoir quel jour et à quelle heure se produit l’équinoxe d’automne, et transcrire ça dans l’heure de Paris puis de débuter une année.
Trouver l’équinoxe relève d’un calcul d’astronomie, et c’est un exercice très complexes : il faut tenir compte de la durée précise d’une année, de la vitesse de rotation de la Terre, de la vitesse de déplacement de la Terre sur son orbite (variable au fil d’une année, et rendue compte grâce à la fameuse équation du temps), de l’inclinaison de la Terre. Puis, pour notre calendrier, de tenir compte de la position de Paris sur la globe.
Cela se fait pourtant. Je n’ai pas tout recalculé moi-même, mais en reprenant un code existant, j’ai reproduit le calendrier sur cette page : Le Calendrier Républicain.
Ainsi, comme j’ai dit en en-tête, la date de publication de cet article aurait correspondu au Duodi 12 Vendémiaire an CCXXXIII. Cela n’a aucune valeur, vraiment, mais c’est un exercice amusant.
À quelle altitude commence le ciel ?
Couleur science par Anonyme le 05/09/2024 à 05:57:00 - Favoriser (lu/non lu)

Le ciel est bleu. Mais d’où vient ce bleu ? Où s’arrête-t-il ? Où commence-t-il ?
Toutes ces questions, plus ou moins métaphysiques, pourraient être posées par un enfant. Mais sont-elles des questions à laquelle un adulte peut répondre ? Pas sûr, car tout va dépendre de ce dont on parle.
On sait pourquoi le ciel est bleu : c’est un phénomène de diffusion différentiée des couleurs de la lumière solaire par les molécules dans l’air, appelé diffusion de Rayleigh. J’explique ça spécifiquement dans mon article : Pourquoi le ciel est bleu ?.
Maintenant, quand on demande d’où vient le bleu, il s’agit de savoir de quel endroit cela vient, et donc au-delà de quel endroit le bleu du ciel n’apparaît plus.
La provenance du bleu
Le bleu provient des molécules de l’air, de toutes les molécules qui diffusent la lumière. Il vient donc essentiellement de partout où il y a de l’air : que ce soient les molécules juste devant vous, ou celles situées beaucoup plus loin. C’est l’effet cumulé du bleu diffusé par toutes les molécules sur toute l’épaisseur de l’atmosphère qui produit la lumière bleue que l’on voit.
Ainsi, naturellement, si l’atmosphère était moins dense ou moins épaisse, ce bleu lumineux serait moins bleu et moins lumineux, c’est-à-dire bleu sombre, voire noire. Et ceci est exactement ce que l’on observe lorsqu’on prend de l’altitude, lorsque la couche atmosphérique au-dessus de nous diminue en épaisseur. L’atmosphère se raréfie également avec l’altitude : l’atmosphère reste soumise à la gravité, comme tout le reste : l’essentiel de l’air se trouve donc proche de la surface terrestre. Sur Terre, il suffit de monter de seulement 5 000 mètres, pour que 50 % de l’atmosphère soit en dessous de nous !
Dans ces conditions, le ciel serait 50 % moins bleu, mais comme les 50 % restants sont du noir (une couleur un peu particulière), la teinte reste clairement bleutée. On ne peut donc dire que le ciel ne soit plus bleu, et donc pas non plus que le ciel commence à 5 000 m.
Rien que sur une montagne moyenne (~ 3 000 m), la perception n’est déjà plus la même qu’au niveau de la mer. En avion, c’est-à-dire à 10 000 m de haut pour un avion de ligne, le ciel est indubitablement bien plus sombre également, mais toujours bleu.
Une altitude à partir de laquelle l’air est trop rare pour que la lumière bleue qu’elle diffuse soit visible correspondrait alors à l’altitude au-delà de laquelle le ciel n’est plus bleu, et donc l’altitude où commence le ciel tel qu’on le voit.
Et la Ligne de Kármán ?
On cite parfois la Ligne de Kármán pour désigner la fin de l’atmosphère. Cette limite est aujourd’hui fixée à la valeur rondelette de 100 km au-dessus du niveau de la mer. Il s’agit d’une limite normalisée et conventionnelle de l’atmosphère, ce n’est pas une limite matérielle ni naturelle.
Pourtant, ça n’a pas toujours été comme ça : la Ligne de Kármán était à son origine une limite physique, d’origine aéronautique.
Pour un aéronef à basse altitude, le maintient en vol est assuré par la portance aérodynamique : l’air est dévié vers le bas par les ailes, ce qui, par réaction, produit une force sur l’avion dirigé vers le haut. L’avion n’a qu’à maintenir sa vitesse pour continuer à dévier de l’air vers le bas et rester en vol.
S’il y a moins d’air à dévier, comme c’est le cas en altitude, cette portance diminue : l’avion doit voler plus vite pour se maintenir. Si l’on continue de gagner de l’altitude, la vitesse doit être d’autant plus élevée.
Dans le cas limite, vu la raréfaction constante de l’air avec l’altitude, cette vitesse de maintien en vol dépasserait la vitesse de libération gravitationnelle. Dans ce cas de figure, l’aéronef se maintient en altitude non plus par les forces aérodynamiques, mais par sa simple inertie : son inertie vers l’avant et sa chute vers le bas (par gravité) sont tels que sa trajectoire suit la courbure de la Terre, et reste donc constamment à la même altitude (malgré sa chute). En un mot : l’avion serait en orbite, et n’aurait plus besoin d’ailes ou même d’air.
Von Kármán avait calculé la limite à partir de laquelle les forces d’inertie sont prépondérantes face aux forces aérodynamiques pour vaincre les forces gravitationnelles et se maintenir en vol, et avait trouvé une valeur de 83,6 km.
Cette valeur avait été recalculée un peu plus tard et trouvée plus proche d’une centaine de kilomètres.
Cette valeur a ensuite été arrondie et normalisée à 100 km.
La Ligne de Kármán existe et est une donnée utile, mais elle ne répond pas à la question cherchant à savoir où s’arrête le bleu du ciel.
La limite du bleu du ciel
Le limite « officiel » entre l’atmosphère et l’espace est, elle, donc, fixée à 100 km d’altitude et dérive de la ligne de Kármán. On est bien dans une situation où l’air s’est considérablement raréfiée et donc où le ciel est très faiblement coloré.
Certaines sources conviennent toutefois que la limite où l’on considère que le ciel est totalement noir est située entre 100 et 160 km. Cette plage est large, car on ne peut pas poser une limite dure sur un dégradé de couleur. Ça serait comme demander à quel endroit termine le bleu et commence l’indigo sur un arc-en-ciel. Cela va dépendre de chacun. Vous pouvez essayer sur l’image d’en-tête : c’est un exercice difficile. Et même en demandant autour de vous : vous aurez sûrement autant de limites différentes que de personnes.
Toujours est-il que la plage allant de 100 à 160 km semble être celle où le bleu n’est plus perceptible : il est si sombre que l’on ne considère plus ça comme du bleu, mais du noir. On peut donc considérer qu’à ces altitudes, on a dépassé la limite du ciel.
Quelques liens
Pourquoi les oignons nous font pleurer ?
Couleur science par Anonyme le 01/08/2024 à 05:52:00 - Favoriser (lu/non lu)

La biologie est une forme de chimie appliquée, dans le sens où les organismes vivants ne sont « que » des tas de molécules dont la cascade de réactions chimiques font ce que nous sommes. Les influx nerveux, la contraction des muscles ou encore la division et la multiplication cellulaire, tout ça est de la chimie.
Dans le cas des oignons qui font pleurer, c’est également une cascade de réactions chimiques qui se produisent.
Les oignons, en tant que plantes, ne peuvent pas s’enfuir face à un prédateur. Et alors que d’autres plantes qui utilisent les animaux pour proliférer (par exemple avec leurs graines qui s’accrochent au pelage pour être semées un peu plus loin), les oignons sont plutôt du genre défensif vis à vis des animaux et vont plutôt se défendre activement des prédateurs plutôt que compter sur eux. L’oignon le fait de façon chimique, en libérant des molécules qui vont venir irriter quiconque essaye de le manger.
Le processus global est une cascade de réactions chimiques qui part de quelques acides aminés pour finir en un puissant lacrymogène.
Quand un oignon est attaqué physiquement, que ce soit par les dents d’un animal ou bien un couteau de cuisine, les cellules libèrent des enzymes, les alliinases qui vont alors agir sur certains acides aminés soufrés, comme la cystéine et l’alliine. Ces enzymes sont alors transformés en acide sulfénique. Cette dernière est instable et se transforme assez rapidement et spontanément en oxyde de propanethial, qui est volatil, c’est-à-dire qu’il passe très facilement en phase gazeuse dans l’air :

Quand les vapeurs arrivent au niveau du visage, elles se dissolvent dans l’humidité des yeux. L’oxyde de propanethial y est alors hydrolysée (elle réagit avec l’eau) en acide propanesulfinique, puis oxydé (elle réagit avec l’oxygène) en acide propanesulfonique. C’est ce dernier qui est irritant pour les yeux, car il stimule leurs récepteurs sensoriels. Le cerveau détecte ça comme une douleur et va actionner le processus de lacrymation, c’est-à-dire de production des larmes, afin de diluer la molécule irritante et de l’évacuer.
Pour s’en protéger lorsque l’on cuisine, une méthode assez connue est de congeler l’oignon, au risque toutefois d’en perdre certaines saveurs. Une autre méthode est de porter des lunettes de protection étanches (lunettes de plongée), ou encore de couper les oignons dans un endroit suffisamment ventilé, pour éloigner et évacuer l’oxyde de propanethial. Utiliser un couteau extrêmement aiguisé peut aussi aider, vu que cela détruira moins de cellules.
D’autres plantes comme l’ail ou l’échalote produisent également de l’acide propanesulfonique lorsqu’elles sont agressées.
Ce système de défense est apparu selon le mécanisme de l’évolution. Que la plante s’est mise à produire les enzymes et les acides aminés sulfoxydés est une chose qui est apparue par le fait du hasard, au fil des générations et des modifications non-contrôlées dans l’ADN de la plante. Mais que les prédateurs s’en retrouvent repoussés, permettant à la plante de mieux survivre et de proliférer est ce qu’on appelle la sélection naturelle (qui elle n’est pas liée au hasard).
Enfin, pour terminer dans une note d’espoir pour les cuisiniers qui n’aiment pas pleurer : certains chercheurs semblent avoir trouvé un moyen de produire des oignons qui ne font pas pleurer. Ils ont réussi cela en retirant le gène responsable de la production de l’alliinases, coupant à la racine (ou au bulbe, en l’occurrence) tout le processus de défense de l’oignon !
Quelques liens
Pourquoi certains nuages sont noirs et d’autres blancs ?
Couleur science par Anonyme le 04/07/2024 à 03:44:00 - Favoriser (lu/non lu)

Pourquoi certains nuages sont blancs et d’autres gris, voire pratiquement noirs ?
Pour faire court, il s’agit d’une question d’épaisseur et de taille des gouttelettes d’eau. Voyons tout ça ici !
Diffusion de Mie & diffusion de Rayleigh
Pour qu’un nuage se forme, de l’air humide — moins dense que l’air sec, contre-intuitivement — doit s’élever dans l’atmosphère. La température diminuant avec l’altitude, il arrive un moment où cette température atteint le point de rosée de l’air qui est en train de monter. Il s’agit de la température à laquelle l’humidité contenue dans l’air se liquéfie et forme de petites gouttelettes d’eau liquide.
Ces gouttes sont beaucoup plus grandes que les molécules d’air ou d’eau en phase gazeuse, par conséquent, les phénomènes de diffusion de la lumière qui entrent en jeu ne sont plus les mêmes non plus. La formation des gouttelettes va en quelque sorte modifier les phénomènes d’interaction entre la lumière et l’atmosphère.
La diffusion de Rayleigh, qui explique la couleur bleue du ciel, n’est valable que pour des particules dont la dimension est inférieure au dixième de la longueur d’onde de la lumière. Les gouttelettes étant bien plus grosses que ça, la diffusion de Rayleigh n’est plus perceptible dans un nuage. Les nuages ne sont donc pas bleus comme le ciel, malgré la transparence effective de l’eau.
Le nuage diffuse toujours la lumière, mais vu que les « particules » sont plus grandes, elles subissent ce qu’on appelle : la diffusion de Mie, et cette dernière ne dépend plus de la longueur d’onde : toutes les couleurs sont autant déviées les unes que les autres.
Le nuage est donc de la couleur de la lumière qui arrive dessus, c’est-à-dire blanche (ou rouge-orange lors des couchers de Soleil).
Les théories de Mie et de Rayleigh sont une seule et même théorie, mais la diffusion de Rayleigh n’est applicable que pour les particules les plus petites (molécules et atomes). Il s’agit d’un cas particulier de la théorie de Mie.
La diffusion de Mie explique la couleur bleue du ciel à cause des molécules nanoscopiques (cas particulier de Rayleigh), et la couleur blanche des nuages, à causes des gouttelettes microscopique, environ 100 à 10 000 fois plus larges.
Et pour les nuages noirs ?
Je l’ai dit plus haut : le nuage, du fait des particules plus grandes que le dixième de la longueur d’onde, prend la couleur de la lumière qui le traverse. S’il n’y a plus de lumière, le milieu est… noir, ou au moins gris foncé, en tout cas notablement plus sombre.
Ceci se produit lorsque la lumière est absorbée avant de parvenir sur le nuage. L’eau des gouttelettes, bien que transparente, finit tout de même par absorber un peu de lumière. Si le nuage est particulièrement épais ou fortement chargé en grosses gouttes d’eau, alors la lumière traverse une quantité significative d’eau et une quantité d’autant significative de lumière est absorbée. Il ne reste alors plus grand-chose sur la partie basse du nuage. Le nuage paraît plus sombre.
Cela peut aussi se produire avec de petits nuages normalement blancs qui passent dans l’ombre d’un gros nuage au-dessus : le petit nuage ne reçoit plus de lumière et apparaît sombre.
Un nuage vraiment sombre est un nuage très chargé en eau, ou très épais. Dans ce dernier cas, ils sont également hauts et leur sommet froid est sujet à une forte condensation de la vapeur d’eau. Dans les deux cas, c’est annonciateur de précipitations imminentes, voire d’orages.
Le même principe peut être appliqué à la fumée d’une cigarette : celle-ci est généralement bleue quand elle s’élève de la cigarette, mais blanche quand elle est expirée. La fumée normale est très fine et diffuse essentiellement le bleu, alors que la fumée expirée est constituée de particules bien plus grosses, formée d’eau agglomérée sur les particules de suie, prenant la couleur de la lumière incidente, c’est à dire blanche.
Liens et ressources
Autres articles sur ce blog :
Comment fonctionnent les piles avec testeurs intégrés ?
Couleur science par Anonyme le 06/06/2024 à 05:23:00 - Favoriser (lu/non lu)

Parmi les piles du marché, on en trouve avec des testeurs intégrés : on appuie sur deux boutons sur la pile, et une jauge indique si la pile est encore bonne (la jauge monte au vert), pas tout à fait pleine (jauge jaune) ou pratiquement vide (jauge rouge). Comment ça marche ?
Encore une fois, personne ne s’est jamais posé cette question, mais je vais y répondre. Vous allez voir, c’est ingénieux et avec plusieurs morceaux de science dedans !
Une encre thermochromique
Ce que l’on voit quand on active le testeur, c’est une jauge qui se colore jusqu’au niveau de charge de la pile. Cette couleur est obtenue par une encre thermochromiques. Ces encres changent de couleur quand elles sont échauffées.
C’est le même type d’encre utilisée dans les tasses thermoréactives, celles qui affichent un motif quand on les remplit d’une boisson chaude.
Leur fonctionnement est détaillé dans mon article sur le fonctionnement des tasses thermoréactives, mais je le rappelle ici.
Les molécules constituantes des encres thermochromiques peuvent être altérées d’une manière réversible par la température. La molécule et sa formule restent les mêmes, mais certaines liaisons chimiques peuvent changer de mode de vibration, ou encore effectuer une rotation sous l’effet de la température : en somme, la molécule peut changer de forme. Ceci modifie alors la façon dont elle absorbe ou émet de la lumière. Autrement dit cela en modifie la couleur.
Certaines encres peuvent être incolores à froid et prendre une couleur vive quand elles sont chauffées. Sur les piles avec les testeurs intégrés, on utilise des encres transparentes à froid qui passent au rouge, jaune ou verte quand elles sont réchauffées.
Utiliser une encre qui change de couleur selon la température, c’est une bonne idée, mais comment produire une chaleur proportionnelle au niveau de charge de la pile ?
Une résistance chauffante à la géométrie particulière
La chaleur, celle qui va colorer les encres thermochromiques du testeur est produite par un circuit résistif simplissime intégré sur la pile. Cette résistance prend la forme d’un simple morceau de papier métallisé très fin.
Quand on appuie sur les deux boutons du testeur, cela court-circuite la pile et fait passer le courant dans le papier métallisé. Ce papier s’échauffe alors et cela colore notre encre. Avec ce principe, on sait que si de la couleur apparaît, c’est que la pile n’est pas morte. Pratique et ingénieux, mais ce n’est pas tout !
On peut donner une forme triangulaire à la feuille métallique. En faisant ça, on a une résistance qui dépend de la position. Lorsque le courant passe, l’échauffement dépendra elle aussi de la position sur la feuille métallique.
En effet, une zone très fine verra tout le courant passer par une faible section et l’échauffement y est donc plus important que dans la zone plus large :

Si la pile est toute neuve, elle peut débiter un courant important. L’intensité échauffera alors toute la longueur et l’encre sera visible sur toute la longueur de la pile.
Si la pile est presque morte, elle débite un courant bien plus faible, à peine suffisant pour ne chauffer que la zone la plus fine de la feuille en métal :

Il suffit alors de placer une couche de peinture thermochromique sur la résistance. Sur la pile pleine, toute la peinture sera colorée, alors que sur la pile vide, seul le bas de la jauge sera colorée et visible.
Améliorons le tout en mettant du rouge en bas de la jauge, du jaune au centre et du vert dans le haut, et on aura une indication rudimentaire, mais tout de même intuitive du niveau de charge de la pile.
Ingénieux non ?
Bien sûr, aujourd’hui il existe des testeurs externes à la pile qui sont essentiellement de petits voltmètres numériques. Mais le système directement intégré sur la pile, même si bourrée de science, reste bon marché et facile à intégrer et à utiliser.
Comment fonctionnent les détecteurs de radon ?
Couleur science par Anonyme le 02/05/2024 à 04:16:00 - Favoriser (lu/non lu)

Certaines communes en France, notamment de Bretagne, ont par le passé distribué des kits de détection du radon, un gaz naturel, mais cancérigène. Sa surveillante est effectuée par l’IRSN : l’Institut National de Sureté Nucléaire, et pour cause, le radon est un gaz radioactif.
C’est quoi le radon ? Comment fonctionnent ces kits ?
C’est quoi le radon ?
Le radon est un gaz radioactif issue de la désintégration de l’uranium présent naturellement dans le sol. L’uranium se désintègre en thorium, qui lui-même se désintègre en protactinium, et de désintégration en désintégration, on arrive sur l’élément du radon :

Le radon se désintègre ensuite lui-même en poursuivant la chaîne de désintégration l’uranium, jusqu’à finir sur le plomb 206, un élément stable, non radioactif.
Étant le seul gaz dans toute celle chaîne, et qui plus est un gaz noble, il est libre de liaisons moléculaires et il finit par émaner du sol et passer dans l’air. Le radon ainsi que sa formation sont naturelles, mais il présente tout de même un risque pour la santé et c’est pour ça qu’il est surveillé, et c’est aussi pour ça que l’on peut se voir proposer des kits de tests par les pouvoirs publics.
Les régions au sol granitique, plus riches en uranium, sont davantage concernées. En ce qui concerne la France, cela correspond essentiellement à la Bretagne, le Limousin, l’Auvergne et le Jura.
Comment fonctionnent les kits de détection ?
Il existe plusieurs méthodes de détection, mais les plus courantes sont les kits de détection à film.
Ces kits portent le nom de « dosimètre radon ». Ils se présentent comme une petite boîte de la taille d’une boîte d’allumettes, à poser ou à accrocher quelque part chez soi, puis, après quelques semaines ou mois, à envoyer en laboratoire pour analyse. Ils sont totalement passifs.
Le principe est similaire à celui du film photographique. Le film photo n’est pas noir, mais il noircit à la lumière, donc lorsque les photons de lumière tapent dedans. Les films des dosimètres radon réagissent, eux, aux particules alpha émises par la désintégration du radon. Chaque particule alpha laisse une trace physique sur le film, dont on mesure ensuite le nombre lors de l’analyse. En tenant compte de la durée d’exposition, le nombre d’impacts ainsi mesuré permet de remonter à la valeur de l’exposition au radon dans le lieu où il fut placé.
Notons que ces dosimètres radon mesurent l’exposition aux particules alpha en général, pas spécifiquement ceux dus au radon. Néanmoins, dans l’air d’une région exposée à ce risque, l’essentiel du rayonnement alpha est produit par le radon et sa chaîne de désintégration. Aussi, le danger provient des particules alpha quelles qu’elles soient, pas spécifiquement du radon.
Conclusion
Ces détecteurs sont au final très simple. Ce sont des films sensibles aux particules alpha.
Les particules alpha sont les moins énergétiques parmi les particules alpha, bêta, gamma émises par la radioactivité. Elles sont stoppées par une simple feuille de papier ou encore un vêtement et sinon par la surface de la peau, mais ce sont aussi les particules les plus massives et à cause de ça, elles peuvent altérer physiquement une surface ou encore une cellule vivante ! Les particules alpha sont environ 5 à 20 fois plus dangereuses pour le vivant que les particules bêta ou gamma, malgré leur énergie bien plus élevée, donc.
Tant qu’il reste en dehors de notre organisme, le radon gazeux ne présente pas de réel danger : la peau nous protège de lui. Les choses sont totalement différentes si le radon est respiré : là, les dégâts qu’elles engendrent se font sur les cellules non protégées. Le radon a un fort potentiel cancérigène parce qu’il est susceptible d’être inhalé et parce qu’il est émetteur alpha.
Le radon est émis par le sol, les murs et en raison de sa densité, il a tendance à se retrouver dans les maisons, notamment les caves si ces dernières sont insuffisamment ventilées.
Le taux de radon dans l’air d’une maison varie d’ailleurs très fortement au cours d’une année et en fonction de la météo : en hiver et lorsqu’il pleut, les maisons sont généralement bien moins ventilées qu’en été et lorsqu’il faut beau temps.
Liens et ressources
- Du radon dans votre maison ? Des kits distribués pour mesurer ce gaz naturel cancérigène ;
- Connaître le potentiel radon de ma commune ;
- Cartographie du potentiel radon des formations géologiques – IRSN ;
- Radon Measurement Method Definitions – The National Environmental Health Association, National Radon Proficiency Program
Comment fonctionnent les revêtements céramiques hydrophobes ?
Couleur science par Anonyme le 04/04/2024 à 03:58:00 - Favoriser (lu/non lu)

Il existe, dans le monde automobile, des revêtements de protection en céramique. Peut-être connaissez-vous le Rain-X® ? Les traitements céramiques ont des propriétés similaires au Rain-X, si ce n’est que c’est encore plus efficace et surtout beaucoup plus durable.
Ces traitements protègent la peinture, mais ils ont aussi un effet hydrophobe et déperlant, particulièrement recherché.
En pratique, l’effet déperlant permet de rouler sous la pluie sans avoir à utiliser ses essuie-glaces, tout en ayant une visibilité bien meilleure que sans le traitement. Sur la carrosserie, le nettoyage au jet d’eau est grandement facilité également : moins de saleté reste collé sur la voiture, et le peu qui y reste se décolle tout seul.
Comment fonctionnent ces traitements ? Comment obtient-on un effet hydrophobe ?
Le phénomène de « mouillage »
Le mouillage désigne le comportement d’un liquide en contact avec une surface solide. Quand les gouttes de liquide tombent sur le solide, on peut distinguer trois possibilités :
- mouillage nul : les gouttes ne collent du tout et roulent (elles « perlent ») sur la surface jusqu’à tomber par terre ;
- mouillage parfait : les gouttes collent parfaitement et s’étalent au maximum, formant un film mince, parfaitement uniforme ;
- mouillage intermédiaire : les gouttes collent moyennement sur la surface, formant des gouttes plus ou moins régulière (c’est ce cas qu’on connaît dans la vie courante).
Pour l’effet déperlant, cela peut faire penser à du mercure sur une surface en plastique, ou encore de l’eau sur les feuilles de certaines plantes comme la tulipe ou le lotus (l’effet lotus). La goutte n’accroche absolument pas à la surface et glisse par gravité.
Pour l’effet d’une goutte qui s’étale au maximum de la surface, voyez votre miroir dans la salle de bain sur lequel vous avez frotté du savon. La buée semble ne pas se poser sur la zone savonnée, mais en réalité, l’eau s’y pose bel et bien.
C’est juste que l’eau ne crée pas de gouttelettes qui déforment l’image, mais un film uniforme qui ne déforme pas l’image dans le miroir. Cet effet provient du savon qui est un tensioactif, c’est-à-dire qu’il diminue drastiquement la tension de surface de l’eau. L’eau n’est donc plus tentée de former des gouttes rondes, mais peut au contraire s’étaler librement pour épouser totalement la forme du miroir, et créer un film très mince. Cet effet du tensioactif est également obtenu avec de l’alcool et certains solvants, et c’est pour cela que les lingettes antibuée pour lunettes contiennent de l’alcool notamment.
Dans le cas des revêtements hydrophobes pour voiture, on recherche l’effet déperlant : que les gouttes ne s’étalent surtout pas mais perlent et tombent, par gravité, entraînant la saleté avec elle.
Une question d’énergie superficielle (ou tension de surface)
Dans une phase condensée (liquide ou solide), il faut distinguer le cœur de la matière d’une part et la surface d’autre part. Dans le liquide par exemple, toutes les molécules sont libres de se déplacer, mais restent attirées les unes aux autres. Cette attraction provient de diverses forces intermoléculaires : forces de London, de Debye et forces de Keesom, regroupées sous le terme de forces de van der Waals.
Une molécule située au cœur de la matière présente ces forces attractives dans toutes les directions, et donc sur toutes les molécules autour d’elles. Une molécule en surface essayera de faire de même, mais n’a pas de molécules à lier au-dessus d’elle (vu que c’est en surface). L’énergie destinée à ces liaisons subsiste « en trop », et elle va être redistribuée sur les liaisons en surface. Ces liaisons sont donc plus fortes à cet endroit :

Les molécules en surface sont donc fortement liées les unes aux autres et forment comme une pellicule ; à un tel point que l’on peut faire flotter des petits objets :

C’est ce phénomène que l’on appelle la tension de surface (ou tension superficielle). Elle résulte du fait que les liaisons intermoléculaires sont plus énergétiques en surface. Ce surplus d’énergie est aussi ce qui forme le ménisque d’eau et le phénomène de capillarité. L’eau est plus stable en se liant au verre avec des liaisons « normales » qu’en créant des liaisons énergétiques avec le reste de l’eau, quitte à devoir vaincre la gravité en remontant sur les bords.
Des choses similaires se produisent dans les solides : les atomes de la surface ont un surplus d’énergie à cause de liaisons qui ne peuvent se former, faute de matière au-dessus. Pour les solides, on emploie le terme d’énergie de surface (surface free energy en anglais). La conséquence de ce surplus d’énergie est que le solide formera des liaisons avec toutes les impuretés qui se posent dessus… et en particulier les liquides !
Interaction d’un liquide sur une surface solide
Lorsqu’une goutte de liquide tombe sur une surface solide, le liquide et le solide vont se lier. Les gouttes restent « collées » à la surface, même si la surface est inclinée verticalement. Ceci rejoint le phénomène de mouillage vu précédemment.
Différents solides peuvent avoir des énergies de surface différentes : certains solides ont des énergies de surface plus importantes que d’autres.
Ainsi, si un solide a une énergie de surface importante, comme c’est le cas d’une façon générale pour les métaux, le solide cherchera à maximiser la surface de contact avec le liquide : le mouillage est favorable et la goutte d’eau s’étale, augmentant d’autant l’adhésion du liquide.
Au contraire, si le solide a une très faible énergie de surface, ce qui est le cas du polytétrafluoroéthylène (PTFE, connu sous le nom de « Téflon », et qui revêt notamment les poêles anti-adhésives), la surface de contact diminue fortement. L’adhésion est plus faible et la goutte ne colle pas du tout à la surface : elle « perle » et tombe, laissant la surface essentiellement sèche et propre.
Ces différents cas sont modélisés par l’angle de contact de la goutte de liquide avec la surface. Dans le cas de l’hydrophobie, la goutte tend à s’arrondir et à former un grand angle de contact :

On comprend ici que si l’angle de contact est grand, le même volume d’eau n’est accroché au solide que par une faible surface : elle peut donc facilement se détacher. C’est l’hydrophobie. Au contraire, un angle de contact faible signifie que la goutte d’eau est aplatie, formant une surface de contact importante et elle est fortement solidaire de la surface.
Et la céramique ? Et les traitements hydrophobes ?
Considérant tout cela, pour obtenir un effet déperlant, on comprend qu’il faut avant tout un revêtement avec une faible énergie de surface. Ce revêtement sera peu enclin à se lier aux liquides, et ces derniers ne seraient pas retenus et perleraient facilement.
Ces matériaux-là incluent ceux utilisés pour les traitements céramiques. Ces produits se composent d’un solvant (de l’alcool isopropylique généralement) dans lequel sont en suspension des nanoparticules de céramique. On entend ici par « céramique » un matériau qui n’est ni organique, ni métallique.
Pour les traitements pour voitures, on a à faire à des nanoparticules de dioxyde de silicium et de dioxyde de titane. Ces céramiques ont une très faible énergie de surface (c’est ce que l’on recherche).
Ces nano-billes, appliquées sur une vitre ou sur une carrosserie, vont se solidariser sur la surface, et former une couche protectrice hydrophobe. L’eau qui tombera dessus ne s’étalera pas, formera de grosses gouttes peu liées à la surface, qui tombent donc très facilement par simple gravité.
Conclusion (et est-ce réellement efficace ?)
Pour résumer, un revêtement céramique avec effet hydrophobe déperlant tire son efficacité des phénomènes à la surface des matériaux : les liaisons inter-moléculaires y sont plus fortes qu’ailleurs. Une goutte d’eau sur le verre va donc avoir tendance à se lier au verre et à rester dessus, même si la surface est inclinée.
En recouvrant la vitre avec un revêtement ayant des liaisons de surfaces plus faibles (l’énergie de surface est plus faible), l’eau n’aura plus tendance à s’étaler et à se coller sur la surface. Elle conservera sa forme de bille sphérique, et perlera sur la vitre, ce qui constitue l’effet tant recherché.
En pratique, les revêtements grand publics diminuent seulement l’énergie de surface sans la faire disparaître totalement. En résulte que l’eau collera juste beaucoup moins, mais l’hydrophobie n’est pas totale.
Néanmoins, ils repoussent toujours beaucoup mieux l’eau qu’une surface normale. Les meilleurs traitements donnent un effet assez spectaculaire et aident réellement lors du lavage ainsi que sous la pluie. De plus, les céramiques utilisées sont essentiellement transparentes, dues à la finesse extrême de la couche posée : 5 à 10 nanomètres. Ils sont prévus pour durer entre 1 à 5 ans.
Généralement, on fait un compromis entre l’hydrophobie et la tenue dans le temps (même si les gammes de produits s’améliorent d’année en années, tant sur la durabilité que l’hydrophobie).
Les revêtements « super-hydrophobes » que l’on voit dans certaines vidéos où l’eau n’accroche absolument pas, sont ce qui se fait de mieux en termes d’hydrophobie. Pour le moment, ces produits issues de la recherche sur les matériaux sont non encore opaques (et donc inadaptées pour une vitre de voiture), mais surtout fragiles : ils ne durent pas dans le temps, en particulier exposées aux UV dehors. Nulle doute qu’un jour, il existera un tel produit à la fois super-hydrophobe et résistant aux éléments (et à un prix convenable pour le public), mais ce produit reste encore à découvrir ou à inventer.
Enfin, ces traitements fonctionnent tant qu’ils ne sont pas totalement usés (après plusieurs années), ou recouverts de saleté incrustées (la saleté très fine finit toujours par s’accrocher partout), or, cette saleté n’est, elle, pas hydrophobe. Si l’effet semble s’estomper un peu rapidement, il est peut-être temps de passer au lavage-auto.
Pour s’amuser
Pour visualiser tout ça, on peut prendre une seringue quelconque et de l’eau. La seringue formera des gouttes d’eau de taille relativement identiques. À partir de là, on peut essayer de faire tomber des gouttes une par une sur des surfaces variées :
- métaux ;
- plastiques ;
- poêle antiadhésive ;
- verre normal ;
- verre frotté avec du savon puis essuyé avec un essuie-tout ;
- verre frotté avec de la cire (d’une bougie, ou cire à chaussure ; puis essuyée également) ;
- verre traité au Rain X.
- …
On peut aussi remplacer l’eau par de l’alcool, du liquide vaisselle, de l’huile…
On constatera assez vite que certaines surfaces tendent à étirer les gouttes d’eau (le verre frotté au savon et les métaux), et d’autres forcent les gouttes à prendre une forme bien ronde (plastiques, poêle, verre traité au Rain X).
Mieux, on peut essayer de souffler sur les gouttes : on verra que les matériaux avec les gouttes les plus arrondies sont plus faciles à sécher : les gouttes partent plus rapidement. Cela est dû à la forme plus bombée de la goutte, offrant une meilleure prise au vent, et à la surface de contact de la goutte, plus faible, donc moins bien « collée ».
Liens et ressources
- Surface energy — Wikipedia ;
- What is surface free energy? — Biolin Scientific ;
- What is Surface Free Energy? — Kyowa Interface Science ;
- Everything You Need To Know About Ceramic Coatings — Engineering Explained — YouTube ;
- Ceramic Coating - How it Works | Science Garage - YouTube ;
- How Ceramic Coating Hydrophobics Work: Auto Detailing Science.
Comment fonctionnent les stylos détecteur de faux billets ?
Couleur science par Anonyme le 07/03/2024 à 17:31:00 - Favoriser (lu/non lu)

Parfois sont utilisés des stylos ou feutres qui détectent les faux billets. L’emploi en est assez simple : on fait une petite marque sur le billet avec le stylo, et il y a alors deux possibilités :
- soit le trait est jaune et disparaît en séchant ;
- soit le trait devient bleu ou noir, et persiste.
Si le trait disparaît, le billet est authentique et la marque ne laisse pas de trace.
Si le trait persiste d’une couleur très sombre, alors le billet est un faux.
Comment cela fonctionne ? Est-ce que c’est fiable ?
Une encre à base d’iode et du papier contenant de l’amidon
L’encre de ces stylos est à base d’eau ou d’alcool et contient de l’iodure de potassium. C’est plus ou moins la même chose que la teinture d’iode utilisée en médecine pour nettoyer une plaie. Concentré, c’est un produit brun-orange. Dilué, il est jaune voire transparent.
L’amidon quant à lui est un polymère du glucose (un sucre) : il s’agit d’un long enchaînement de molécules de glucose. Ces longues chaînes peuvent être ramifiées ou s’enrouler en hélice. Dans le cas où elles forment ces chaînes hélicoïdales, on parle d’amylose.
Quand on met en présence des ions iodure I− avec de l’amidon, et plus spécifiquement de l’amylose, les ions iodure viennent se placer au centre de l’hélice d’amylose :

Ce complexe ainsi formé absorbe la lumière et devient donc très sombre : bleu foncé, voire noir. Cette coloration disparaît si l’on chauffe la solution : les hélices d’amylose ont alors tendance à se dérouler.
Le test de l’iode est une méthode très connue et très simple pour mettre en évidence la présence d’amidon. Il est utilisé par exemple par les brasseurs de bière, pour vérifier que l’amidon a bien été complètement transformé en sucres simples (qui seront ensuite fermentés par les levures, ces dernières ne pouvant consommer l’amidon directement).
Du papier utilisé pour les billets de banque
OK, donc l’iode réagit avec l’amidon. Et nos billets ?
La plupart des billets de banque du monde, incluant ceux en euros et en dollar, sont imprimés sur de la fibre de cellulose, typiquement de coton. Ces derniers ne contiennent pas d’amidon. Si l’on verse de la teinture d’iode sur ces billets, cela ne devient pas bleu-noir, mais reste jaune puis disparaît en séchant.
Le papier ordinaire, en revanche, contient de l’amidon ! Si l’on verse de l’iode dessus, cela fera une tache sombre. Il en ira de même pour une pomme de terre, de pâtes alimentaires ou encore du pain : on met facilement leur amidon en évidence grâce à de la teinture d’iode que l’on verse dessus :

Ce que font donc ces stylos, c’est détecter l’amidon. Si un billet contrefait est imprimé sur du papier ordinaire, il contiendra de l’amidon et le stylo laissera une trace noire. Si le billet est authentique, il sera imprimé sur de la fibre de cellulose et le stylo ne laissera pas de marque noire.
Est-ce fiable ?
Comme toutes les méthodes de détection, elles sont fiables seulement jusqu’à un certain point, et ne sont donc pas parfaites. Il est possible de faire passer des faux-billets comme étant des vrais (faux-négatifs) et inversement détecter des vrais billets comme étant des faux (faux-positifs).
Si le billet contrefait est imprimé sur du papier de coton, alors le stylo ne les détectera pas. De plus, il est facile de traiter un papier ordinaire pour qu’il ne réagisse pas à l’iode. Par exemple avec un acide. Le fameux « tour de magie » qui permet d’écrire avec du jus de citron (contenant de l’acide citrique) utilise ce principe : on passe un pinceau d’iode dessus et les zones écrites à l’acide ressortent clair alors que la feuille noircit.
Un billet authentique qui a été contact avec de l’amidon (farine ou pain chez le boulanger par exemple) apparaîtra également comme un faux billet à cause de l’amidon contenu dans la farine. Il faut vraiment ne pas avoir de chance, mais cela peut arriver.
En cas de doute, il faut utiliser une technique de vérification complémentaire, comme un détecteur à ultra-violet (les billets contiennent des bandes fluorescentes sous UV), un détecteur magnétique (certaines encres des billets sont sensibles aux aimants), ou encore un test de transparence (certaines zones sont plus ou moins transparentes.
Quoi qu’il en soit, c’est une méthode intéressante et à portée de tout le monde pour résoudre un problème de la vie de tous les jours et impliquant de la chimie.
Liens
Moyenne, médiane, écart-type & mode
Couleur science par Anonyme le 01/02/2024 à 05:01:00 - Favoriser (lu/non lu)

En statistiques quand on veut parler d’une série de valeurs, comme des salaires d’un ensemble de personnes, on parle souvent de la moyenne de ces salaires.
Cette moyenne n’est pourtant pas toujours très représentative, et c’est très facile à constater :
Si Bill Gates entre dans un bar, en moyenne, tout le monde est milliardaire.
Bien-sûr, on comprend tout de suite ici que la valeur de la moyenne prise seule n’est pas très intéressante : elle n’est pas du tout représentative de quoi que ce soit dans ce bar.
Elle n’est pas inutile pour autant : on peut la comparer à la moyenne des salaires des gens du bar d’en-face, où ne se trouve pas Bill Gates, mais en pratique ce n’est pas ce que nous faisons. Dans la vie courante, on voit la moyenne des salaires et on se compare à cette moyenne, et on se déclare alors riche ou pauvre (pour caricaturer).
Heureusement, la moyenne n’est pas le seul indicateur pour résumer une série de valeurs. D’autres indicateurs existent. Cet article est là pour les présenter. Après une définition précise de la moyenne, on verra la médiane et le mode. La notion d’écart-type et de dispersion seront également présentés.
La moyenne
La moyenne est toujours située entre les deux valeurs extrêmes (le minima et le maxima) de la série. On dit qu’il s’agit d’un indicateur de position.
La moyenne — plus précisément la moyenne arithmétique, car il en existe d’autres : géométrique, harmonique, pour ne citer qu’elles — d’une série de nombres est habituellement notée $\bar{x}$, ou M. Il s’agit de la somme de toutes les valeurs xi d’une série, divisée par la taille n de la série de valeurs :
$$\bold{M} = \bar{x} = \frac{1}{n}\displaystyle\sum_{i=1}^n{x_i}$$
D’un point de vu plus matériel, ou physique, il s’agit aussi du barycentre non pondéré, ou isobarycentre, de la série de points.
La moyenne représente une valeur qui tient compte de l’ensemble des éléments, même ceux qui sont clairement erratiques ou absurdes. Elle est très sensible aux valeurs extrêmes. Elle est représentative d’un ensemble, mais pas forcément des éléments individuels dans cet ensemble : l’exemple plus haut avec Bill Gates le montre bien.
Parfois, un indicateur qui soit plus proche des valeurs individuelles est plus représentative de la réalité.
La médiane
La médiane, également un indicateur de position, est un exemple généralement plus représentatif des valeurs individuelles. Pour la trouver, il faut que la série de nombres soit trié dans l’ordre.
Si la taille de la série de nombres est impair, alors la médiane est le nombre pile au milieu de la série triée.
Si la taille de la série de nombres est pair, alors la médiane est la moyenne des deux nombres centraux de la série triée :
$$M = \begin{cases} x_{\frac{n+1}{2}} &\text{si n impaire} \\ \\ \frac{ x_ {\frac{n}{2}} + x_{\frac{n}{2}+1} }{2} &\text{si n pair }\end{cases}$$
La médiane sépare la liste en deux portions de même effectif.
Par exemple, dans un ensemble de 7 valeurs ordonnées, la médiane est la quatrième valeur. Dans un ensemble de 8 valeurs, la médiane est la moyenne arithmétique entre la quatrième et la cinquième valeur.
L’avantage de la médiane c’est qu’elle est représentative des valeurs centrales d’une série de nombres. Elle est insensible aux extrêmes. Dans notre exemple avec Bill Gates, bien que son salaire soit astronomique, la médiane n’est toujours décalée que d’une place dans la liste des salaires de toutes les personnes dans le bar.
Dès lors, si le bar est rempli de personnes qui gagnent entre 2 000 et 3 000 €, que l’on fasse entrer un millionnaire, ou un milliardaire, ou même un multi-milliardaire, la médiane ne sera toujours que déplacée d’une place. Les valeurs extrêmes, pour peu qu’elles ne soient pas nombreuses, n’ont pas d’influence notable.
Dans une série statistique, la médiane, contrairement à la moyenne, permet d’éliminer une bonne partie de l’influence des valeurs parasites, ou aberrantes.
Le mode
Le mode correspond à la valeur la plus représentée dans une série de nombres. Dans une série de nombres dont on compte les occurrences de chaque valeur, le mode est la valeur avec la plus forte occurrence. Il s’agit de la valeur dominante.
Contrairement à la moyenne et à la médiane, le mode n’est pas toujours défini : si les valeurs d’une série de nombre sont toutes différentes, aucun n’est plus représenté que les autres. Le mode est alors indéterminé.
Dans notre exemple du bar, si l’on a deux personnes à 2 000 €, trois à 2 500 € et Bill Gates, le mode sera 2 500 €, car il y a plus de personnes qui touchent ce salaire-là que n’importe quel autre salaire. Le mode donne une indication de la majorité : le salaire de 2 500 € est le salaire majoritaire (majorité relative).
L’écart-type et l’étendue
On a constaté que la moyenne, la médiane et le mode permettent de se situer au sein d’un ensemble de valeurs statistiques. On dit que ces grandeurs sont des indicateurs de position.
Pour être plus précis dans ce dont on parle, on doit compléter ça par un indicateur de dispersion, c’est-à-dire une grandeur qui indique l’écart d’un indicateur de position par rapport aux valeurs réelles. Cet indicateur de dispersion nous donne des informations sur l’homogénéité de la série de valeurs.
Une moyenne (et ça vaut aussi pour une médiane) doit toujours être accompagnée de l’information sur la dispersion des valeurs autour de la moyenne. Cette dispersion est calculée en analysant les écarts de chaque valeur à la moyenne.
Il existe plusieurs façons de parler de cet écart à la moyenne, mais la plus courante est évidemment l’écart-type. Les informations que sont la valeur minimale et la valeur maximale, ainsi que l’étendue, peuvent aussi être très utiles.
L’écart-type
Sur un ensemble de valeurs xi, situées autour d’une moyenne $\bar{x}$, on peut mesurer les écarts de chaque valeur à moyenne :
$$e_i = x_i - \bar{x}$$
Puis faire la moyenne ē de ces écarts :
$$\bar{e} = \frac{1}{n}\displaystyle\sum_{i=1}^n{e_i}$$
Sauf que… cette valeur est toujours nulle ! En effet, ces écarts — qui peuvent être positifs ou négatif — se compensent dans l’ensemble à cause de la définition même de la moyenne $\bar{x}$.
Si l’on veut une donnée qui ne soit pas nulle, les écarts doivent être absolus. Pour cela, on peut par exemple prendre les carrés des écarts (pour tout passer en positif) avant d’en prendre la moyenne. Notons V cette nouvelle valeur :
$$\bold{V} = \frac{1}{n}\displaystyle\sum_{i=1}^n{(e_i)²}$$
V est appelé la variance. Si cette indication peut être utile, le fait de mettre au carré mettrait aussi au carré d’éventuelles unités. Pour un salaire en euros (€), l’unité de la variance serait des euros² (€²). D’un point de vue métrologique ou même à l’usage, c’est peu pratique.
Une possibilité est alors de prendre la racine carrée de la variance, ainsi on retombe sur des unités identiques à celle des grandeurs étudiées. Notons σ (« sigma ») la racine de la variance :
$$\sigma = \sqrt{\bold{V}}$$
Cette nouvelle valeur, σ, est ce qu’on appelle l’écart-type, et elle a la même unité que les valeurs étudiées (des euros dans notre exemple).
Pourquoi ne pas prendre la valeur absolue des écarts ?
On peut se demander pourquoi ne prend-on pas la moyenne des valeurs absolues des écarts, plutôt que faire des carrés puis des racines, ce qui reviendrait au même en termes d’unités. Et c’est une bonne question.
Sachez que l’on peut prendre la moyenne des valeurs absolues. On obtient alors non pas l’écart-type, mais l’écart moyen, noté $\bold{EM}$. On parle aussi de la déviation absolue à la moyenne. Ça existe, mais ça n’a pas toutes les propriétés de l’écart-type.
Avec l’écart moyen, on prend la valeur absolue de chaque écart à la moyenne, et on en fait la moyenne :
$$\bold{EM} = \frac{1}{n}\displaystyle\sum_{i=1}^n{|x_i - \bar{x}| }$$
En notant que la valeur absolue d’un nombre est la racine carrée du carré de ce nombre — $|x| = \sqrt{x^2}$ — on peut l’écrire aussi :
$$\bold{EM} = \frac{1}{n}\displaystyle\sum_{i=1}^n{\sqrt{(x_i - \bar{x})^2}}$$
Avec ce mode de calcul, tous les écarts ont le même poids dans la moyenne : il n’y a aucune pondération. C’est parfois voulu, mais pas toujours.
L’écart-type, lui, passe par le carré de l’écart, puis en fait la moyenne, et enfin seulement fait la racine carrée de cette moyenne. En mettant au carré un écart déjà important, on amplifie cet écart : on le pondère.
L’écart-type est donc la moyenne pondérée des écarts, et le facteur de pondération l’est par leur propre valeur : chaque écart est pondéré par lui-même, à cause du carré.
Si le constat est fait que l’écart-type et l’écart moyen sont très différents, cela signifie qu’il y a quelques valeurs qui sortent du lot. Ceci permet entre autres de repérer des valeurs parasites, ou aberrantes.
Qui plus est, l’écart-type représente parfaitement la distribution des valeurs dans le cas d’une distribution Gaussienne (ou distribution normale, une notion très importante en statistiques). Les intervalles de confiance (68 %, 95 %, 99 %, etc) fonctionnent avec l’écart-type, et non l’écart-moyen. Le symbole de l’écart-type — σ, sigma — est d’ailleurs celui auquel on réfère quand on parle des intervalles de confiance 1σ, 3σ, 5σ…
Enfin, le calcul de l’écart type est une fonction dérivable, alors que l’écart moyen ne l’est pas : la fonction valeur absolue n’est pas dérivable en 0. Mathématiquement, cela peut avoir son importance dans le cas où l’on veut étudier les fonctions issues des calculs statistiques sur un ensemble de données.
Quelle différence réelle entre l’écart moyen et l’écart-type ?
À titre de note à part, pour ceux pour qui ce serait nécessaire, insistons vraiment sur ceci : la moyenne des racines des carrés des écarts à la moyenne (l’écart moyen) n’est pas la même chose que prendre la racine de la moyenne des carrés des écarts à la moyenne (l’écart-type) :
$$\sigma = \sqrt{\frac{1}{n}\displaystyle\sum_{i=1}^n{(x_i - \bar{x})²}}$$
$$\bold{EM} = \frac{1}{n}\displaystyle\sum_{i=1}^n{\sqrt{(x_i - \bar{x})²}}$$
Ces deux formules sont différentes car l’ordre des opérations a son importance : la racine d’une moyenne n’est pas la même chose que la moyenne des racines (essentiellement parce $\sqrt{a+b} \not = \sqrt{a} + \sqrt{b}$).
L’écart-type est généralement la plus utilisée des deux.
L’étendue
L’étendue est la différence entre la valeur la plus grande et la valeur la plus petite de la série de données. C’est assez simple à comprendre, mais il permet de constater l’homogénéité (ou non) d’une série de données, et de fournir des informations sur les extrêmes.
Par exemple, toujours dans l’exemple du bar avec les salaires, si le salaire moyen est de 2 000 €, et que l’étendue est de 100 €, cela signifie que tous les salaires sont compris dans une fourchette de 100 €. Par exemple, de 1 950 € à 2 050 €, ou encore de 1920 à 2 020 €. Si l’étendue est faible, ça veut dire que tout le monde touche à peu de choses près le même salaire.
Dans le cas où Bill Gates rentrerait dans le bar, l’étendue serait quasiment égal au salaire max (le sien), ainsi qu’à la somme de tous les salaires. Ceci indique l’existence d’une valeur totalement aberrante/
L’étendue est quelque chose d’important qui ne peut pas être obtenue autrement, même avec l’écart-type. On peut avoir deux séries de valeurs avec les mêmes écarts-types et les mêmes moyennes, mais avec des étendues très différentes.
Cette information n’est apportée que par l’étendue, d’où l’importance de noter les valeurs maximales et minimales d’une série de données, en plus de la moyenne, y compris accompagnées de son écart-type.
Exemples
Exemple 1 : salaires de deux entreprises
À titre d’exemples pour tout ça, considérons deux entreprises de mille employés chacune : l’entreprise A et l’entreprise B. La distribution des salaires se fait de cette façon :
| Employé | Salaire |
|---|---|
| #1 | 500 € |
| #2 | 2 000 € |
| … | … |
| #999 | 2 000 € |
| #1000 | 3 500 € |
| Moyenne : | 2 000 € |
| Médiane : | 2 000 € |
| Mode : | 2 000 € |
| Écart-type : | 67,115 € |
| Min : | 500 € |
| Max : | 3 500 € |
| Étendue : | 3 000 € |
| Employé | Salaire |
|---|---|
| #1 | 1 900 € |
| #2 | 1 900 € |
| … | … |
| #225 | 1 900 € |
| #226 | 2 000 € |
| … | … |
| #550 | 2 000 € |
| #551 | 2 100 € |
| … | … |
| #1000 | 2 100 € |
| Moyenne : | 2 000 € |
| Médiane : | 2 000 € |
| Mode : | 2 000 € |
| Écart-type : | 67,115 € |
| Min : | 1 900 € |
| Max : | 2 100 € |
| Étendue : | 200 € |
On constate ici que les salariés de ces deux entreprises ont des salaires bien différents, pourtant les valeurs des moyennes, médianes et écart-types sont identiques ! Seuls changent ici les étendues et les valeurs des salaires le plus bas et le plus haut de l’entreprise.
Pour l’entreprise A, on pourrait penser que le salaire « type » est de 2 000 ± 67 € grâce à la moyenne et l’écart-type, mais dans l’absolu, on aura tout de même un écart de 3 000 € entre le salaire le plus bas et le salaire de plus haut. Cela peut être piégeux.
L’entreprise B, avec le même nombre d’employés, mais avec une distribution des salaires différente, aura un salaire moyen toujours égal à 2 000, et un écart-type de 67 € également, mais l’étendue sera seulement de 100 € ! D’un point de vue de l’égalité des salaires, cette seconde entreprise semblerait mieux : il n’y a aucun salaire qui se détache réellement de l’ensemble : tout est compris dans une fourchette plutôt restreinte.
Exemple 2 : séries de lancers de deux dés
Un exemple plus aléatoire, si on peut dire : le lancer de deux dés.
Si on lance un seul dé, on a autant de chances de faire n’importe quel chiffre de 1 à 6. Si maintenant on lance 2 dés, la valeur la plus probable est le 7, tout simplement, car le nombre de combinaisons qui font 7 est plus importante que toutes les autres : 1+6, 2+5, 3+4, 4+3, 5+2 et 6+1 font tous 7, alors que pour faire un 12, il n’y a que la combinaison 6+6 qui fonctionne. Dans le cas de deux dés, toutes les valeurs ne sont pas équiprobables.
Voici le résultat de 100 lancers de dés :
| Somme obtenue | Fréquence |
|---|---|
| 1 | 0 |
| 2 | 4 |
| 3 | 6 |
| 4 | 10 |
| 5 | 10 |
| 6 | 13 |
| 7 | 17 |
| 8 | 13 |
| 9 | 12 |
| 10 | 10 |
| 11 | 4 |
| 12 | 1 |
Si on visualise ça graphiquement, on constate que cela se rapproche d’une fonction gaussienne (ou loi normale). Cela signifie que les dés ne sont pas truqués et que les lancers sont bien dus au hasard :

Cette tendance est renforcée si l’on augmente le nombre de lancers (ou le nombre de dés à chaque lancer), ici le résultat de 10 000 lancers de deux dés, ainsi que le résultat de 10 000 lancers de quatre dés (donc des résultats de 4 à 24).
Conclusions
Il y a différentes valeurs à sortir d’une série statistique. Toutes ont leur raison d’être et toutes apportent une information pertinente au sujet de la série de valeurs, en particulier concernant la dispersion (écart type, étendue…) et la tendance centrale (moyenne, médiane…).
Dans l’exemple ci-dessus, on voit aussi que plusieurs séries statistiques peuvent partager certaines grandeurs (avoir la même moyenne et écart-type) mais être totalement différentes dans d’autres (étendue, valeur min, valeur max).
Certaines valeurs sont également inutiles si on les complète pas par une autre. L’exemple de la moyenne dans un bar avec Bill Gates est relativement parlant. Ici, l’information de la moyenne est totalement absurde : elle ne donne aucune information sur le salaire de chacune des personnes se trouvant dans le bar, mais plutôt une information sur la somme totale des salaires de toutes les personnes qui s’y trouvent. Une moyenne sans son écart-type, ou sans la médiane n’est généralement pas utile. Il ne faut s’en souvenir à chaque fois que l’on lit un article de presse qui parle, par exemple, du salaire moyen qui monte malgré la crise, ou du coût « moyen » de la vie.
Liens
Comment fonctionnent les canettes et plats auto-chauffants ?
Couleur science par Anonyme le 04/01/2024 à 03:02:00 - Favoriser (lu/non lu)

Le commerce regorge de gadgets étranges qui font selon moi vendre davantage pour leur côté insolite que pour le côté réellement utile.
L’un de ces produits est la canette de café auto-chauffante. Il s’agit d’une canette à première vue ordinaire (si ce n’est du café), mais qui avec un simple bouton arrive à la réchauffer en quelques instants. Ce n’est pas aussi pratique qu’une bouteille dite isotherme, et forcément beaucoup plus cher, mais le fonctionnement le rend à lui seul intéressant et mérite donc un petit article.
On peut aussi trouver des plats de nouilles chinoises ou d’autres denrées dans des emballages « auto-chauffants ».
Comment réchauffer une canette ?
Il y a plusieurs façons d’avoir un dispositif auto-chauffant. Le meilleur exemple est probablement celui des chaufferettes de poche, dont il existe un bon nombre de sortes. Ceci peut être notre point de départ pour étudier l’idée et voir si cela suffit pour réchauffer un plat ou une boisson.
Certaines chaufferettes de poche fonctionnent avec des piles lithium, et pourraient être adaptées pour chauffer une canette. Pour un objet à usage unique, cela ne serait toutefois ni écologique ni économique.
Ni même assez puissant, d’ailleurs : une canette de 250 mL remplie d’une boisson à base d’eau que l’on souhaite chauffer de 10 à 60 °C requiert une énergie de 52 kJ. Si on avait un dispositif avec une batterie lithium, il faudrait une batterie de 3 000 mAh pour cela, soit autant qu’une batterie de téléphone, ce qui coûterait cher pour une canette. Il faudrait en plus que l’énergie soit libérable en quelques minutes seulement, ce qui n’est pas tellement possible avec cette technologie.
On pourrait utiliser la méthode des chaufferettes catalytiques Peacock ou Zippo. Ces chaufferettes fonctionnent grâce à une décomposition d’un hydrocarbure catalysé par du platine (un métal précieux et rare). Là aussi ce n’est pas économique (le platine coûte très cher), et il y a un risque avec le combustible à base de naphta, qui est toxique et volatile. La quantité de chaleur produite reste également faible.
Un dernier exemple issu d’un troisième type de chaufferettes est d’utiliser le principe des chaufferettes « chimiques » liquides. Ces chaufferettes renferment une pièce métallique à cliquer : dès le clic, le liquide cristallise en libérant une chaleur douce autour de 54 °C. C’est économique et non-polluant, mais la quantité de chaleur produite est très limitée, nettement insuffisante pour chauffer une boisson comme le café. En effet, l’eau possède une bien trop grande capacité thermique, ce qui nécessite beaucoup d’énergie pour en augmenter la température ne serait-ce que de quelques degrés.
On voit dans les exemples précédents que le principal problème technique est la quantité de chaleur à produire.
Pour réaliser un chauffage « portable » qui chauffe beaucoup et très vite, il faut quelque chose de plus puissant. Quelque chose impliquant de la pyrotechnie ! La chimie a ce qu’il faut : parmi les solutions retenues par les fabricants de ces canettes, on distingue deux méthodes.
La méthode à l’oxyde de calcium
L’oxyde de calcium, de formule chimique CaO, est aussi appelée de la chaux vive. La même qu’utilisée en construction. Elle réagit vivement avec l’eau, en produisant de la chaux « éteinte » et de la chaleur par la réaction :
$$\text{CaO} + \text{H}_2\text{O} → \text{Ca(OH)}_2$$
En construction, la chaux éteinte employée réagit ensuite très lentement (plusieurs semaines, mois) avec le dioxyde de carbone de l’atmosphère pour produire du carbonate de calcium, du calcaire, relativement dure, suffisamment en tout cas pour servir d’enduit sur les murs.
Dans notre canette, c’est la chaleur produite qui est intéressante : celle-ci est émise en quelques instants. Quand elle est produite à l’air libre, cette réaction peut monter à 250 °C. Au sein d’une canette, l’eau de la boisson absorbe cette énergie en s’échauffant, et monte assez vite à 50-60 °C.
Les canettes utilisant la chaux vive ont une petite capsule de chaux et une petite poche d’eau au fond de la canette. L’activation se fait en écrasant la poche d’eau dans l’oxyde de calcium, ce qui amorce la réaction et démarre le processus de réchauffement de la boisson, qui dure alors 2 à 3 minutes.
Note : la chaux vive isolée doit être maniée avec précaution, car c’est un produit caustique et irritant, en plus de réagir de façon exothermique avec l’eau. La réaction peut projeter des vapeurs brûlantes et irritantes.
La méthode à la thermite
Une autre méthode, bien plus fun, est d’employer de la thermite ; le même explosif que celui utilisé pour souder des rails de chemin de fer ou démolir des bâtiments.
Enfin presque.
La thermite est le nom générique d’une réaction entre un métal et l’oxyde d’un autre métal. La plus connue est la réaction de l’aluminium et l’oxyde de fer, le tout en poudre, et qui va produire une réaction au cours de laquelle l’oxygène est transféré du fer à l’aluminium, libérant au passage une grande quantité de chaleur :
$$\text{Fe}_2\text{O}_3 + 2 \text{Al} → 2 \text{Fe} + \text{Al}_2\text{O}_3$$
Ici, le fer obtenu est généralement liquide et à plus de 2 000 °C :

Une petite quantité suffirait donc pour chauffer une boisson.
La réaction de la thermite de fer et d’aluminium est cependant bien trop violente. On va donc lui préférer une alternative, à savoir l’oxyde de silicium et l’aluminium :
$$3 \text{Si}\text{O}_2 + 4 \text{Al} → 3 \text{Si} + 2 \text{Al}_2\text{O}_3$$
La réaction est un peu moins vive, mais produit toujours une quantité importante de chaleur. Le fait de réduire la vitesse de la réaction permet à cette chaleur d’être captée par la boisson avant que la capsule qui renferme la réaction ne fonde ou n’explose.
Dans ces canettes, l’activation se fait en tournant la base de la canette. Ceci allume une mèche qui va initier la réaction de la thermite. Cette réaction se produit au sein d’une capsule métallique en contact avec la boisson. La capsule sert à la fois à isoler la boisson des réactifs et à conduire plus facilement la chaleur vers la boisson.
En quelques instants, la boisson est réchauffée.
Il est à noter que la boisson absorbe toute cette chaleur. Si l’on vide la canette avant, la chaleur n’est pas dissipée et s’accumule dans les réactifs, ce qui fait monter la température très haut, assez pour faire fondre l’aluminium de la capsule, donc à plus de 660 °C.
Conclusion
Contrairement aux chaufferettes pour les mains (que ce soit avec une batterie au lithium, à l’acétate de sodium, ou les chaufferettes catalytiques…) pour lesquelles la chaleur douce est émise de façon prolongée dans le temps, les deux méthodes que sont la chaux vive ou la thermite permettent de chauffer fortement sur une courte période.
Le reste est une question de dosage : on veut un produit qui chauffe la canette de façon décente aux alentours de 50-60 °C, sans non plus tout vaporiser.
Liens
Il existe un brevet sur le principe de ces canettes chauffées à la thermite.
Ci-dessous quelques liens vers des vidéos ou les produits auto-chauffants (canettes, nouilles…) directement. Ce ne sont pas des liens sponsorisés :
- Complete Instructions On How +42º Self Heats Beverages Work (par The 42 Degrees Company, qui produit ces canettes) ;
- Heating Coffee with Thermite! (vidéo de démontage d’une canette à la thermite) ;
- Pour les noodles, cherchez « Instant HotPot Noodles — Google ».
Et des liens vers d’autres articles sur ce site, dont ceux des différents types de chaufferettes :
- Comment fonctionnent les chauffes-mains catalytiques Peacock® ou Zippo® ? ;
- Comment fonctionnent les chaufferettes de poche ? ;
- Comment fonctionnaient les lampes à acétylène ? (un dispositif utilisant non pas l’oxyde de calcium, mais le carbure de calcium).
Pourquoi y a t-il du givre sur votre voiture alors qu’il fait +4 °C ?
Couleur science par Anonyme le 07/12/2023 à 19:35:00 - Favoriser (lu/non lu)

Vous avez sûrement déjà eu à gratter votre pare-brise de voiture le matin en hiver, pour enlever le givre. Le givre est simplement de la glace apparue par condensation de l’humidité de l’air sur une surface particulièrement froide, comme votre vitre.
Peut-être avez-vous remarqué que, parfois, du givre soit apparu quand bien même les températures n’ont pas été négatives au cours de la nuit.
Comment est-ce possible ? Comment la glace peut-elle se former si l’air est à +4 °C ?
Ce phénomène curieux, bien réel, se produit par la combinaison de plusieurs facteurs.
De la mesure de la température par les services météo
La température donnée par la météo est la température de l’air. Celle de Météo France l’est dans des abris météo standardisées, appelés abri Stevenson, et qui contiennent toute l’instrumentation météorologique. Ces abris sont peints en blancs, protègent de la pluie et des rayons directs, sont situés entre 1,5 et 2,0 mètres de hauteur par rapport au sol, mais laissent quand-même passer l’air. C’est de cet air qui passe que la température, l’hygrométrie et la pression sont captées.
Cette mesure ne correspond pas toujours à la température ressentie ou obtenue par un thermomètre grand public. Une voiture stationnée au soleil sera plus chaude. Un thermomètre accroché sur un mur ou un arbre à l’ombre sera plus froid.
Si votre météo vous dit +4 °C, la température à certains endroits de votre allée ou de votre jardin peut être parfois différente, y compris la température réelle (pas seulement la température ressentie).
Ceci étant dit, cela ne suffit pas toujours à expliquer le givre. Parfois, l’air est réellement à +4 °C partout et pourtant vous devez gratter la voiture.
Rassurez-vous : la thermodynamique va bien. C’est juste qu’une partie des phénomènes en jeu sont bien cachés.
De l’hygrométrie au cours d’une journée
En journée, l’air est plus chaud que la nuit. Il peut donc capter plus d’eau, ce qu’il fait. Durant la nuit, la température baisse et la même quantité d’eau arrive saturer l’hygrométrie. À ce point, on a atteint le « point de rosée » et l’eau doit sortir de l’air. Il va alors condenser en gouttelettes et tomber sur les différentes surfaces disponibles : l’herbe, le sol, votre voiture… L’eau vient donc de là.
S’il ne fait pas trop froid, l’eau restera là comme telle, c’est-à-dire liquide. Mais s’il fait sous les +4 °C, qu’il n’y a pas trop de vent, et surtout que le ciel est dégagé, les choses se gâtent.
Une question de rayonnement perdu
Généralement, tous les objets au repos et à un même endroit sont à la même température : c’est l’air qui participe à transporter la chaleur entre les objets et à égaliser les températures : on parle de conduction thermique par convection de l’air.
S’il n’y a pas de vent, la convection est réduite et les températures ne s’équilibrent plus très bien. Il faut alors prendre en compte un autre phénomène : le rayonnement thermique.
Tous les corps rayonnent de la chaleur, essentiellement par infrarouge. Le rayonnement est fonction de la température : plus un corps a une température élevée, plus le rayonnement est important. Si des braises nous apparaissent chaudes même à distance, c’est à cause du rayonnement qu’elles émettent. D’ailleurs, quand on dit que les braises sont rouges voire jaunes, c’est que la température est suffisante pour émettre non seulement des infrarouges, mais aussi de la lumière rouge, de plus en plus lumineuse, jusqu’à devenir jaune, blanche…
Ce rayonnement, s’il est capté par un autre corps, peut le réchauffer : ce qui est perdu par l’un est alors gagné par l’autre. Deux objets en vis-à-vis vont finir par équilibrer leur température par un échange de lumière infrarouge.
À présent, si vous placez un objet en direction du ciel la nuit, il rayonnera de l’infrarouge vers l’espace, mais ne recevra rien en retour : il y a bien l’air, mais ce dernier rayonne peu par rapport à un objet solide ; le vide sidéral, lui, ne rayonne rien.
En d’autres termes, votre surface exposée à l’espace va refroidir.
S’il n’y a pas beaucoup de vent, le refroidissement par rayonnement va être plus important que le réchauffement par conduction par l’air.
Lorsqu’il fait entre 0 et +4 °C, cette baisse de température engendrée par le rayonnement perdu dans l’espace est suffisant pour que la surface exposée au ciel passe sous les 0 °C. Si de la buée tombe dessus, elle formera du givre et vous devrez gratter… même si l’air un peu plus loin est à une température positive !
Vous constaterez d’ailleurs que le pare-brise gèle beaucoup plus facilement que les vitres latérales, qui ne sont pas autant exposées au ciel. De surcroît, les vitres latérales sont exposées aux murs, aux buissons, haies, qui rayonnent aussi et réchauffent les vitres, empêchant le givre voire toute condensation de se former !
Vous pouvez donc prévenir la formation de givre en stationnant votre voiture face à un bâtiment ou à un arbre par exemple : ces derniers vont rayonner des infrarouges vers votre vitre et cela suffira pour maintenir la vitre au-dessus de 0 °C. Cela marche très bien, parfois même quand l’air est quelques degrés en dessous de zéro !
Le rayonnement et la perte thermique vers l’espace fonctionne évidemment en l’absence de nuages. S’il y a des nuages, ces derniers captent le rayonnement et renvoient le leur vers le sol, réchauffant le pare-brise et empêchant le givre. Pour cette raison, vous constaterez que les matins où vous devez gratter, sont les matins de nuits claires et sans nuages.
Pourquoi un miroir sèche-t-il toujours du bas vers le haut ?
Couleur science par Anonyme le 02/11/2023 à 04:15:00 - Favoriser (lu/non lu)

Parmi les petits mystères de la vie courante, il y a celui de la buée sur le miroir de votre salle de bain : ce dernier sèche toujours du bas vers le haut. La frontière entre la région sèche et la région humide remonte le miroir au cours du séchage. Le séchage n’est donc pas uniforme : il se fait spécifiquement dans ce sens-là.
Cela peut être surprenant si l’on considère que l’air chaud monte, et donc que le haut devrait être plus chaud, et donc moins sujet à accumuler de la buée (la buée s’accumule préférentiellement sur les surfaces froides).
Si cette remarque reste juste, que l’air chaud — pas la chaleur — monte bien, votre miroir est essentiellement à la même température quel que soit l’endroit où l’on en mesure la température. D’une part, parce que le miroir conduit la chaleur d’un endroit à un autre jusqu’à s’équilibrer, et d’autre part parce qu’il est généralement accroché à un mur, et que ce dernier a une température relativement uniforme.
L’autre problème avec l’hypothèse précédente, c’est qu’elle ignore l’élément principal dans toute cette histoire : l’humidité !
Une histoire de densité des gaz
Contrairement à ce que l’intuition pourrait nous suggérer, l’air humide chargée en vapeur d’eau, n’est pas plus dense que l’air sec. Bien au contraire : l’air humide est plus léger que l’air sec. La raison est liée à la molécule d’eau elle-même, et à la façon dont les gaz se mélangent.
La molécule d’eau est une molécule très légère. Sa masse molaire est de 18 g/mol, contre une moyenne de 29 g/mol pour l’air.
Aussi1, si l’on ajoute un gaz A dans un gaz B, sans changer la pression globale, alors c’est comme si une molécule du gaz B était remplacée par une molécule du gaz A. Le remplacement se fait typiquement d’une molécule pour une molécule, quel que soit le gaz (ce principe dérive de la loi d’Avogadro-Ampère qui dit qu’un volume donné de gaz à des conditions de température et de pression données comportera le même nombre de molécules quel que soit le gaz en question).
De l’air humide n’est donc pas de l’air dans lequel on ajoute de l’eau, mais de l’air dans lequel on remplace un peu de l’air par de l’eau. Cela revient donc à remplacer une molécule de 29 g/mol par une molécule de 18 g/mol : la densité globale de l’air dans lequel on injecte de l’eau en devient plus faible.
En d’autres termes, la vapeur d’eau allège la densité de l’air.
Mécanique de l’air humide
Si l’air humide est moins dense, il s’élève. Dans une pièce fermée comme une salle de bain humide, l’humidité a donc tendance à s’accumuler au plafond. Si l’on continue de produire de la vapeur d’eau, la quantité d’air humide augmente et chasse l’air sec en dessous. Un miroir qui se trouverait exposé à cette humidité s’embue donc en commençant par le haut, jusqu’à s’embuer à un niveau de plus en plus bas.
Lorsqu’on quitte la salle de bain et que l’on ouvre la porte, l’air sec et froid du couloir arrive par le bas et c’est donc aussi le bas du miroir qui reçoit de l’air sec en premier. L’humidité sur ce dernier s’évapore dans l’air sec et le miroir sèche en bas.
Enfin, au fur et à mesure que l’air humide quitte la pièce par le haut, l’air sec remonte dans la pièce, séchant le miroir par le bas.
La même chose se produit quand on active la ventilation (VMC) : cette dernière aspire l’air humide au niveau du plafond et de l’air sec le remplace en passant sous la porte, à nouveau par le bas.
Dans tous les cas donc, l’humidité reste en hauteur et le haut du miroir sera le dernier à être exposé à l’air sec, et donc le dernier à sécher.
Notons toutefois que si l’on laisse l’air de toute la maison se mélanger, l’humidité finira par se diluer peu à peu sur toute la hauteur de la pièce, mais cela prend du temps. Beaucoup plus que pour sécher un miroir.
Conclusion
Quand on cherche à comprendre un phénomène, il est très important de tenir compte de tous les facteurs. La chaleur, l’air chaud, monte, oui c’est vrai. Mais ce n’est pas le principal élément en lien avec l’air humide d’une salle de bain. Ce titre revient, précisément, à l’humidité. Et dans le cas de l’air, l’humidité agit de façon très particulière sur l’air et notamment sa densité.
Dans cet exemple, l’air humide est moins dense que l’air sec, et donc il monte, et il commence donc par embuer d’abord le haut d’un miroir ou d’une vitre. Et lors du séchage, l’air humide stagne aussi plus longtemps en hauteur, et c’est également la dernière zone à sécher : c’est la raison pour laquelle le miroir sèche en bas d’abord puis en haut.
Un autre exemple simple, mais fascinant sur cette idée où il faut voir la totalité d’un phénomène avant de tirer une conclusion, c’est celui du thermomètre de Galilée, dans lequel, malgré les apparences, la densité des capsules colorées ne change pas en fonction de la température !
Notes
1 : Dans l’approximation des gaz parfaits, généralement appliqués pour les gaz « simples » comme ici.
Autres articles
Sur ce blog, et au sujet des miroirs, qui sont fascinants :
L’origine astronomique d’Halloween
Couleur science par Anonyme le 05/10/2023 à 05:12:00 - Favoriser (lu/non lu)

Dans mon article dédié à l’origine de Noël, j’explique comment une fête astronomique païenne avait donné peu à peu Noël ; les chrétiens n’ayant en effet rien inventé. Eh bien, de façon surprenante ou non, on peut retrouver quelque chose de similaire avec Halloween : l’origine de cette fête résiderait également dans les étoiles !
Rappel sur Noël
Pour rappel, la fin du mois de décembre était remplie de festivités à travers toute l’Europe et même l’Égypte antique : à cette époque de l’année en effet, le Soleil commençait à remonter dans le ciel après plusieurs mois où il ne faisait que baisser. De même, les jours commençaient aussi à se rallonger.
La fin du raccourcissement des jours, et la remontée du Soleil sont marqués par le solstice d’hiver, autour du 21 décembre. Comme le changement de course du Soleil prend toujours quelques jours avant d’être visible, c’était généralement vers le 25 décembre que l’on comprit que les beaux jours allaient revenir.
N’oublions pas qu’on est dans l’antiquité. Ceci était perçu comme un bon présage et donnait donc lieu à des festivités, telles que les saturnales, ou le nouvel an romain.
Plus tard, l’Église plaça ses propres fêtes au même endroit afin de profiter de leur popularité et mieux s’assouvir à travers l’Europe.
Et Halloween ?
Pour Halloween, c’est un peu similaire. L’on ne considère maintenant plus le Soleil, mais plutôt certaines étoiles et constellations.
Une histoire de constellation et de mythologie
L’évolution a donné à notre cerveau une tendance naturelle à reconnaître des formes un peu partout : dans les nuages, dans les étoiles, la forme des rochers ou des arbres. On appelle ça la paréidolie.
Quand on vit dans l’antiquité et que l’on observe le ciel nocturne, on ne voit pas des étoiles comme nous aujourd’hui. On y voit des points, que l’on peut relier, pour former des figures.
Et lorsque nous vivons entourés de chiens nouvellement domestiqués, d’ours, de taureaux, et que nos histoires et contes font mentions de géants, de héros et de divinités, alors on les imagine aussi dans les étoiles au dessus de nous.
C’est de là que viennent les constellations (du latin « con- », un ensemble, et « stella », étoiles), que ce soit l’Aigle, le Grand Chien, Orion le chasseur, la reine Cassiopée, la Grande Ourse, etc.
Qui sait si celles-ci avaient été imaginées à notre époque : aurions-nous la constellation de l’avion, du smartphone, du four à micro-ondes ?
À cause de notre révolution autour du Soleil et de l’inclinaison de notre écliptique, la position et la hauteur des constellations varie au cours de l’année. Chacune des constellations est à son point le plus haut ou son point plus bas une fois dans l’année, et chaque année à la même période. C’est la base de l’astrologie.
Ce phénomène cyclique et annuel, nous donne une horloge cosmique, racontée par ces personnages de la mythologie qui sonnent par exemple l’arrivée de l’hiver ou de l’été, et donc la période des semis ou des récoltes, très importantes.
La constellation des Pléiades pour Halloween
Prenez la constellation des pléiades. Il s’agit d’un ensemble très rapproché de 6 étoiles (sept à l’époque antique) facilement reconnaissable. Elle est juste à côté du taureau et de la constellation d’Orion, dont on reconnaît la ceinture très rapidement, formée de trois étoiles alignées et très lumineuses :

Selon la mythologie grecque, Orion, le chasseur légendaire, tomba sous le charme de sept jeunes femmes, sept sœurs en vérité : les sept filles de Pléione et d’Atlas.
Orion les poursuivit inlassablement durant sept années entières.
Épuisées, les Sœurs demandèrent grâce à Zeus, qui la leur accorda : il les transforma en étoiles dans le ciel, les mettant à l’abri d’Orion. La constellation des sept sœurs, les Pléiades, était ainsi formée.
Les anciens apportaient une grande importance aux Pléiades, qui est une des constellations les plus faciles à repérer dans le ciel. On la retrouve ainsi dans la grotte de Lascaux, chez les Mayas, et dans le monde moderne sur le logo de Subaru, qui est aussi le nom japonais de la constellation.
Au cours d’une année, cette constellation apparaît le matin ou le soir. Le moment où elles commencent à se lever avant le Soleil, les rendant visibles, annonçait le printemps puis l’été. Elle se lève alors de plus en plus tôt dans la nuit, jusqu’à se lever la veille au soir, puis carrément se lever avant même le coucher du Soleil.
Ce dernier moment, où elles se lèvent avant que le Soleil ne se couche marquait l’automne et annonçait l’hiver.
Plus précisément, le moment où les Pléiades commence à se lever lors du Soleil couchant se trouve au milieu de l’automne, et plus précisément vers la fin du mois d’octobre. Cette apparition dans le ciel était alors saluée par la fête des morts.
Pour la petite histoire, Orion était vantard de ses prouesses de chasse, ce qui déplut à Héra. Pour le punir, cette dernière ordonna à un scorpion de piquer Orion quand il ne s’y attendait pas. Et cela arriva : Orion, le chasseur légendaire, mourut tué par un petit animal. Il fut alors transformé en constellation, juste à côté des pléiades… Héra remercia le scorpion en le transformant en constellation également, mais pour éviter que le combat entre le bête et Orion ne s’éternise, plaça le scorpion de l’autre côté de la voûte céleste.
La fête des morts et l’Halloween
Tout comme pour Noël et la position du Soleil, donc, le lever des Pléiades le soir était l’occasion d’une célébration, en l’occurrence celle des défunts, et elle se tenait donc lieue fin octobre à cause de la date où son lever coïncide avec le coucher du Soleil.
Cette fête correspond aujourd’hui à celle de la Toussaint et de la fête des morts, placées respectivement au 1ᵉʳ Novembre et au 2 novembre dans notre calendrier.
Notons au passage que la Toussaint se dit « All Hallow’s » en anglais.
Logiquement, la veille de la Toussaint — le soir où les Pléiades sont observables — correspond au 31 octobre. Autrement dit une date appelée « veille de la fête de la Toussaint », ou « All Hallow’s Eve », en anglais, dont l’expression a fini par évoluer en « Hallowe'en » avec le temps.
Et nous y voilà : Halloween représentant la veille au soir de la fête de la Toussaint (elle-même veille de la fête des morts), et placée le jour de l’année où la constellation de la Pléiade se lève au moment où le Soleil se couche.
Liens & ressources
- Pleiades: The Seven Sister Stars on Halloween | The Old Farmer's Almanac
- Pléiades: les sept sœurs étoiles de l'Halloween - Les jardins de Laurent
- Les Pléiades (mythologie et histoire des constellations)
- Orion et les pléiades
- Les Pléiades : joyau du ciel d’hiver | Espace pour la vie
- Orion, les Hyades et les Pléiades - Clodoweg
- Orion — Wikipédia
- Halloween — Wikipédia
- Subaru — Wikipédia
Comment communiquer avec une civilisation extra-terrestre ?
Couleur science par Anonyme le 07/09/2023 à 06:15:00 - Favoriser (lu/non lu)

En 1972 et 1973 furent lancées les sondes Pioneer 10 et 11 en vue de la reconnaissance, pour la première fois, des confins du système solaire et des planètes géantes. La destinée de ces sondes, après leur mission, était de s’éloigner indéfiniment de la Terre, toujours plus profondément dans l’obscurité de l’espace…
À l’époque de leur lancement, nous ne savions pas si nous étions seuls dans l’univers ou non. Nous ne le savons d’ailleurs toujours pas aujourd’hui. Ceci n’a pas empêché la NASA d’accrocher notre « carte de visite » sur les sondes Pioneer sous la forme de la célèbre plaque de Pioneer :

Cette plaque comporte, de façon codée, la position du Soleil dans la galaxie, la position de la Terre dans notre système solaire, ainsi que la silhouette d’une femme et celle d’un homme. Le tout était destiné à une éventuelle civilisation extra-terrestre si elle trouvait notre sonde.
Cette opération fut renouvelée, sous la forme d’un disque doré à l’occasion des sondes Voyager. D’un côté, le disque comportait un enregistrement de bruits et sons rencontrés sur Terre (paroles, bruits d’animaux, de machines…). De l’autre côté, des instructions codées sur la façon de lire le disque et restituer les sons, ainsi que des informations similaires à celle de la plaque de Pioneer :

Citons enfin un autre message dans ce style, à savoir le message d’Arecibo, transmis sous la forme d’un signal radio binaire, un peu comme du morse très basique. Une fois reconstitué, le message devait subir un décodage, mais servait de nouveau à distribuer notre adresse galactique.
Les chances que ces « bouteilles à la mer » dans un océan cosmique soient trouvés et décodés semblent infimes, et encore plus infime d’aboutir sur la visite d’extra-terrestres sur notre planète.
Dans ce cas, pourquoi donc avoir laissé ces messages ? Et comment faire en sorte qu’ils soient déchiffrables par d’autres êtres vivants ? C’est l’objet de l’article.
Pourquoi chercher à se faire trouver ?
Si l’on examine la façon dont les êtres humains ont considéré leurs territoires à peine conquis au fil de l’histoire, on note très vite que ça s’est généralement terminé dans le sang et la destruction.
Pas juste sur les autres tribus humaines, mais aussi sur les autres espèces animales : nous tenons des animaux en esclaves dans des cirques, nous les maltraitons parfois, les exploitons souvent pour leurs œufs, viande, fourrure, huile, ivoire… et nous les exterminons même pour la menace qu’ils représentent pour nous ou nos intérêts, et même les tuer pour notre simple et égoïste plaisir sadique.
De surcroît, nous ignorons quasi systématiquement l’effet que nos activités ont sur les autres espèces. À tel point que nous sommes actuellement dans la sixième extinction massive d’espèces vivantes ; et celle-ci porte notre nom, et possède l’être humain pour cause directe : l’extinction de l’Anthropocène.
Au vu de tout cela, posons-nous la question suivante : si nous nous accordons le droit de faire subir ce qui précède aux autres espèces moins intelligentes, à quoi devons-nous nous attendre de la part d’une civilisation plus intelligente, si ce n’est qu’elle nous traite comme nous traitons les animaux ?
On peut cependant porter un espoir à ça.
En effet, si une civilisation extraterrestre arrive à venir nous rendre visite en traversant la galaxie, elle serait forcément beaucoup plus avancée que nous, puisque nous-même sommes encore à des siècles (au moins !) de pouvoir en faire autant. On peut alors nourrir l’espoir qu’une civilisation plus avancée soit également plus sage et plus bienveillante que l’espèce humaine, et qu’elle ne pense donc pas immédiatement à nous tuer et à nous exploiter.
Cet espoir a de bonnes chances d’être comblé : car après tout, la sagesse et la retenue sur nos instincts destructeurs est une condition nécessaire pour survivre à soi-même suffisamment longtemps pour maîtriser le voyage interstellaire. En ce qui nous concerne, bien qu’à l’aube d’une destruction sans précédent de l’écosystème de notre planète, nous sommes — globalement — plus sages que nos ancêtres.
Notre considération envers les uns et les autres, les peuples et tribus variées, les animaux et les autres espèces, s’améliore petit à petit. On est loin d’une grande harmonie, mais l’avenir s’annonce meilleur — ou moins mal — que le passé sur ces plans-là. Les guerres sont moins nombreuses, les gens sont plus coopératifs entre-eux et nous sommes plus que jamais proches d’une gouvernance mondiale, à la fois politique (avec l’ONU), que technologique et culturel (Internet, par exemple), scientifique (LHC, ISS), sportive (les JO), économique… malgré quelques tensions de temps en temps.
Envoyer notre adresse dans le cosmos peut sembler un pari risqué, que nous avons choisi de prendre, car nous n’avons en vérité rien à perdre ! Ce « pari » est également justifié par le fait que n’importe quel signal électrique que nous ayons émis au cours de l’histoire rayonne déjà dans l’espace autour de nous. Une civilisation qui passe dans notre voisinage galactique peut capter n’importe quelle émission de TV ou de radio qui a été émise par le passé. Un émetteur de signal TV émet partout, y compris dans l’espace, et qu’on le veuille ou non.
Considérant ça, pourquoi ne pas leur transmettre un message pacifique ? Cela ne coûte rien.
Comme expliqué plus haut, les civilisations enclines à venir nous trouver ont de bonnes chances d’être pacifiques, et de toute manière, aurait la technologie de venir nous voir, y compris sans notre aide.
Quelle difficulté de communiquer avec les extra-terrestres ?
Il subsiste un problème : comment communiquer avec une civilisation extra-terrestre ? Ils ne parlent (a priori) pas français, ni anglais, ni aucune langue humaine. Il est illusoire de penser qu’ils partagent même l’un de nos alphabets.
En fait, la « barrière de la langue » avec un extra-terrestre est bien plus énorme et fondamentale encore que cela.
Communiquer avec des extra-terrestres
Avez-vous déjà essayé de communiquer avec une taupe ou un cerisier ? Dire que ce n’est pas simple est pour le moins un euphémisme. Pourtant ces deux organismes partagent plus de la moitié de leur ADN avec nous. Même discuter avec un grand singe — qui a 97 % de l’ADN en commun avec un humain — reste difficile, et seuls certains résultats très basiques peuvent parfois être obtenus.
Encore mieux : avez-vous déjà essayé de communiquer avec un être humain vivant de l’autre côté d’une frontière ? Dans une autre langue ? Seule une minorité de personnes sont capables de le faire facilement. Et l’on parle ici d’individus de la même planète et de la même espèce.
Comment pouvons-nous espérer un seul instant discuter avec un être qui a évolué à l’autre bout de la galaxie ? On peut imaginer autant de formes de vie que l’on veut, mais dans la majeure partie des cas, la communication sera extrêmement difficile, voire impossible.
Un problème allant jusqu’à la physionomie
Dans les films de science-fiction, les aliens sont toujours de forme humanoïde, marchent comme des humains, respirent, voient et parlent comme nous, et comprennent toujours notre langue. Bref, ce sont des humanoïdes colorés en bleu ou en vert, rien de plus.
D’un point de vue scénaristique, cela s’explique parfois par le fait que ça se passe dans le futur, et que ces extra-terrestres sont en fait d’anciens humains qui ont évolué de leur côté après un voyage dans l’espace durant des siècles et que l’on retrouve par hasard. C’est une possibilité scénaristique tout à fait crédible, mais qu’en serait-il d’extra-terrestres qui n’ont rien avoir avec nous ?
D’un point de vue exobiologique, il n’y a aucune raison pour qu’une créature extra-terrestre nous ressemblent. Rien que sur la Terre, tous les animaux sont différents, sans même parler pas des plantes ou des bactéries. On trouve dans nos jardins des organismes plus différents de nous que ne le sont les extra-terrestres d’Hollywood !
La réflexion peut aller loin : la vie peut apparaître sur une planète errante, profitant de sa chaleur interne et non de celle d’une étoile. Dans ce cas, la planète est éternellement dans l’obscurité. Ces créatures n’ont donc aucun besoin d’yeux comme les nôtres et n’aura jamais évolué pour en avoir. Même chose si la créature s’est développée sur une planète sans atmosphère : dans ce cas, les sens de l’odorat, de l’ouïe ainsi que la voix seraient inutiles et ne se seraient pas développés.
Ils pourraient en revanche communiquer par le toucher au moyen de vibrations (directe ou via le sol), transferts chimique (comme une synapse), par signaux électriques, magnétiques, infrarouges, etc. Rien de compréhensible par des humains.
Il n’y a aucune raison qu’un extra-terrestre soit humanoïde. Certains pourraient ressembler à des ballons flottant dans l’atmosphère, comme une méduse flotte dans l’eau, ou encore à des formations statiques, à la façon d’un arbre sur Terre. Saurions-nous au moins reconnaître cela comme de la vie ?
Encore une fois, cela va bien au-delà de ce qu’on peut imaginer : ces quelques exemples ne sont que le début des bizarreries que l’on pourrait trouver.
Quoi leur communiquer ?
Pour le disque de Pioneer ou la plaque de Voyager, nous avons donc dû faire des choix. L’univers est trop vaste et sûrement trop créatif pour pouvoir faire quelque chose qui s’adapte à tout ce que l’on peut imaginer, et encore plus pour s’adapter à tout ce que nous n’imaginons même pas.
On peut donc considérer que la seule barrière retenue dans ces messages est la barrière de la langue, pas la barrière des sens par exemple, comme expliqué ci-dessus.
Sur Terre, toutes les civilisations humaines ont utilisé les arbres et les pierres pour créer des habitations et des outils. Nous foulons le même sable et respirons le même air. Nous avons en commun notre planète.
Toutes les civilisations ont utilisé les étoiles pour tracer des constellations, créer des histoires et des mythes. Nous avons en commun la voûte céleste au-dessus de nos têtes.
Plus fondamentalement, nous subissons les mêmes lois physiques aussi.
Dans le cas des extraterrestres, il en va de même mais à une échelle plus grande. Nous ne visons pas sur la même planète, ou dans le même système solaire, mais dans le même univers, celui constitué de 73,9 % d’hydrogène, 24 % d’hélium, 1 % d’oxygène, 0,5 % de carbone et des traces de tout le reste. L’univers étant isotrope et homogène, nous rencontrons les mêmes formations stellaires et galactiques et nous sommes soumis aux mêmes lois de la nature où que l’on se trouve.
C’est donc dans ce qui nous unit que nous devons écrire un message.
Nous connaissons les lois de la physique. Alors eux aussi. C’est donc avec la science que nous communiquerons.
Des êtres intelligents vont forcément chercher à comprendre comment fonctionne leur monde, d’où il vient, de quoi il est fait. Or, en ayant évolué dans le même univers que nous, ils auront les mêmes conclusions que nous : les mêmes lois de la thermodynamique, de l’électromagnétisme, de chimie, etc. Avec des créatures que tout oppose mais avec qui nous partageons un univers, les maths sont notre alphabet et la physique notre histoire.
Pour la plaque de Pioneer et de Voyager, et dans le message d’Arecibo, c’est ce que nous avons utilisé.
Exemple de la plaque de Pioneer
La plaque de Pioneer représente notre adresse cosmique au sein de notre galaxie, la Voie Lactée. En effet, sur l’échelle de notre espèce humaine, le plaque restera dans notre galaxie. Il faudrait bien plus de temps pour qu’elle en sorte. Même la lumière mettrait plusieurs millions d’années pour atteindre seulement la galaxie voisine de la nôtre, sans même parler du reste de l’univers.
Pour commencer, la plaque représente ce que l’univers a de plus abondant : l’atome d’hydrogène. La plaque en représente deux, sous forme d’un proton entouré d’une orbitale électronique :

Les électrons uniques de l’hydrogène sont représentés avec de sorte de flèche orientée. Ceci représente le spin de l’électron, qui peut prendre deux valeurs que nous appelons habituellement haut et bas. Il se trouve que le spin de l’électron de l’atome d’hydrogène change de sens selon une fréquence très régulière de 1 420 405 751,768 Hz, soit 1,42 GHz.
Cette fréquence, la plus rencontrée dans l’univers à cause de l’abondance de l’hydrogène, est donc à coup sûr connue par quiconque étudie le cosmos. Sur le message, cette fréquence donne notre tempo, notre base de temps.
À présent, le message donne également notre position. Similairement au système GPS sur Terre, on peut imaginer un système de positionnement galactique. Plutôt que d’utiliser des satellites dont la position est connue, nous utilisons des astres émetteurs de radiofréquences très régulières : les pulsars. Chaque pulsar est unique et sa position peut être détectée par n’importe qui. Notre position est donc triangulée (trilatérée, pour être précis) par rapport à ces pulsars.
La fréquence propre de ces pulsars est notée comme un multiple de la fréquence de l’hydrogène donnée ci-dessus. Sur le schéma du message, ceci est représenté par les pointillés émanant d’une sélection de quelques pulsars et se rejoignant en un point qui est la position du Soleil :

À ce stade, si une civilisation au moins aussi intelligente que nous a repéré tous les pulsars et noté leur fréquence, ils savent lesquels on a dessiné et pourront utiliser le schéma pour nous positionner dans la galaxie. Ceci en considérant évidemment que les pulsars n’ont pas changé de position au sein de la galaxie. Cela est vrai sur une échelle de temps de quelques millions ou dizaines de millions d’années, mais guère au-delà. Les pulsars et même nos constellations auront changé dans le futur lointain, car toutes sont en mouvements les uns par rapport aux autres dans notre galaxie.
Une autre information, de taille, si j’ose dire, est celle de la longueur d’onde de la fréquence citée. Dans le vide, elle est d’environ 21,1 cm. Ceci représente alors une unité de longueur. Pas besoin de faire intervenir des mètres ou des centimètres, qui sont des unités anthropologiques, on utilise simplement la longueur d’une pulsation de la fréquence de base de l’hydrogène parcourue avec la lumière.
Ceci nous permet par exemple de mesurer la grandeur des deux silhouettes humaines également dessinées.
Il va de soi que le codage des messages doit se faire correctement, et que ça semble assez « tordu ». Maintenant, peut-on vraiment faire mieux, sachant que l’on s’adresse à des êtres qui n’ont pas notre alphabet ni même nos chiffres ? Il est donc obligatoire de passer par des dessins et des schémas, si possibles simples, et en n’employant que des éléments connus dans tout l’univers, à savoir une base scientifique et un codage mathématique ?
Quant à l’usage du binaire dans la représentation des données numériques, elle fut choisie, car je rappelle que la base décimale n’est utilisée que parce que l’on possède 10 doigts en tant qu’humain, et que ce n’est donc pas forcément le cas chez des extra-terrestres. Le binaire quant à lui est plus universel de ce côté-là.
Conclusion
Quand il s’agit de communiquer avec des extra-terrestres, ce n’est pas aussi simple que d’écrire un message et d’en envoyer la lecture dans le cosmos. Déjà, le message doit être capté techniquement, mais aussi décodé, et le résultat du décodage doit lui aussi être lisible par des extraterrestres.
À quoi bon envoyer un message audio si le message est trouvé par un organisme qui n’a pas d’oreilles ? Et ensuite, dans quelle langue l’envoie-t-on ?
Le travail nécessaire pour créer un message, et son support, ainsi que son encodage est donc plus compliqué que ce que ça en a l’air. On considère cependant que le dénominateur commun parmi toutes les civilisations jugées « intelligentes » est la recherche de la connaissance et l’étude de l’univers. Autrement dit, la science.
C’est donc avec cela que les messages sont écrits. Quant au contenu, la seule chose utile envoyée dans les différents messages est notre position dans la galaxie, dans l’espoir de finir éventuellement sur une rencontre.
Comment fonctionnent les tapis rafraîchissant pour chien ou chat ?
Couleur science par Anonyme le 03/08/2023 à 06:41:00 - Favoriser (lu/non lu)

Parlons encore une fois de ces objets de la vie courante qui renferme un peu de science, à l’instar des ventilateurs pour poêle, des sprinklers ou des cocottes minute. Cette fois-ci parlons des tapis rafraîchissants pour chiens ou chats.
Ce sont des tapis à poser par terre et dès qu’on se pose dessus, ils donnent une sensation de froid très prononcé. En période caniculaire, on peut les utiliser sous son oreiller, ou alors les laisser à nos animaux de compagnie qui les apprécient également.
Comment ça marche ? Comment produisent-ils du froid ?
Le problème de produire du froid
Produire du froid n’est pas aussi simple que produire du chaud.
Pour produire de la chaleur, on doit transformer une énergie (électrique, chimique…) en chaleur (énergie thermique), et… c’est tout.
Pour faire du froid, ce mécanisme ne fonctionne pas. On ne peut pas produire du froid par conversion d’électricité en froid : ça ne se fait pas, la nature ne fonctionne pas comme ça. La nature même de la chaleur et du froid ne le permet pas.
Le froid et le chaud n’ont pas de sens en physique : ces deux choses sont identiques : de l’énergie thermique. Un corps froid a simplement moins d’énergie thermique qu’un corps chaud.
Ce que l’on sait faire, c’est déplacer de l’énergie thermique d’un endroit et l’évacuer ailleurs. L’endroit en question finira alors par refroidir. C’est ainsi que fonctionnent les climatiseurs, les frigos, les modules Peltier…
Les tapis rafraîchissants fonctionnent sans piles et encore moins avec un mini frigo : ils sont parfaitement passifs.
D’ailleurs… ils ne produisent pas de froid !
Une simple impression
Les tapis pour animaux ne produisent pas de froid. Vous avez bien lu. Ils sont à la même température que le reste. La sensation de froid est une impression. Cela n’empêche pas que ce soit efficace pour se rafraîchir.
En fait, c’est exactement comme marcher pied nu sur le carrelage, qui semble beaucoup plus froid que marcher sur un tapis. Le carrelage et le tapis sont à la même température, mais les deux n’agissent pas de la même façon en ce qui concerne la chaleur du pied.
Quand on marche sur le tapis, le pied réchauffe le tapis et le tapis maintient ensuit le pied chaud : on peut marcher sans se geler les pieds. La chaleur émise par le pied reste à proximité de celui-ci. Le tapis isole thermiquement le pied chaud du sol froid, et la chaleur reste dans le pied :

Si on marche sur le carrelage, la sensation est autrement plus froide, car le carreau absorbe très rapidement la chaleur et la dissipe dans le sol. Le carrelage est un bon conducteur de chaleur et ne demande qu’à conduire la chaleur de vos pieds dans le sol.
La chaleur de votre pied finit alors par être diffusé dans le sol et le pied par refroidir :

Quand je parle d’isolant ou de conducteur thermique, cela réfère à la notion de conductivité thermique, tout comme on peut parler de conductivité électrique.
Conductivité thermique, convection thermique ou capacité thermique ?
La conductivité thermique permet d’exprimer la quantité d’énergie thermique (de chaleur) qu’un matériau peut conduire d’un endroit à un autre par unité de temps. L’énergie thermique est essentiellement associée à de l’énergie vibratoire dans les molécules. Si les molécules transmettent cette vibration de proche en proche aux molécules voisines, alors l’énergie thermique finit elle aussi par être véhiculée.
Les métaux font ça très bien. Si on chauffe l’extrémité d’un bout de cuivre, l’autre extrémité devient très rapidement chaude également. Si vous cuisinez, vous le constatez facilement avec une cuillère en métal plongée dans une casserole. À l’inverse, une cuillère en bois ne se réchauffe pas aussi rapidement : le bois ne conduit pas bien la chaleur.
Ce n’est cependant pas la meilleure méthode pour transporter la chaleur. On peut transporter beaucoup plus d’énergie thermique si on déplace un corps chaud d’un endroit en un autre. En effet, transporter de la matière chaude d’un endroit à un autre est généralement plus efficace que laisser la chaleur se conduire toute seule d’un endroit à un autre. On parle alors de convection, lorsqu’il y a déplacement de matière en plus de chaleur.
Enfin, le transport de chaleur est également amélioré avec des matériaux qui peuvent absorber de grandes quantités de chaleur. Plus un matériau peut absorber de calories avant de s’échauffer, plus on peut véhiculer de chaleur à l’aide de ce matériau. L’eau est très bonne pour ça : l’eau peut emmagasiner beaucoup d’énergie thermique. Bien plus que de l’acier ou du cuivre !
L’eau doit absorber 4,18 joules par gramme pour monter d’un degré. Le cuivre, avec les mêmes 4,18 joules, monterait de 11 degrés ! Dit autrement, transporter de l’eau chaude véhicule plus de chaleur que transporter du cuivre chaud.
En plus, la fluidité de l’eau lui permet de se mettre en convection et de transporter la chaleur encore plus facilement. C’est pour ça qu’on préfère utiliser des fluides quand on a besoin de refroidir des choses, comme un PC (par water-cooling) ou un moteur de voiture (avec le liquide de refroidissement).
Et nos tapis rafraîchissants ?
Les tapis sont remplis d’une sorte de gel, à base de polymères mais aussi à base d’eau.
L’idée est de tirer parti de tous ces phénomènes cités plus haut à la fois. L’eau, tout d’abord, peut absorber de grandes quantités de chaleur. Quand on pose la main sur le tapis, une grande quantité de chaleur est transmise au tapis… ce qui a pour effet de refroidir la main !
L’eau et le gel dans le tapis sont partiellement liquides: ils peuvent donc se déplacer au sein du tapis : l’eau réchauffée par votre main est alors déplacée et de l’eau fraîche vient prendre sa place se mettre sous votre main, et l’on sent à nouveau du froid.
Enfin, le tapis étant grand et en contact avec le sol et l’air, toute la chaleur absorbée est également évacuée grâce à une grande surface d’échange thermique avec l’extérieur. Le tapis offre donc une sensation continue de fraîcheur.
Une autre explication possible
En faisant les recherches en ligne pour expliquer la sensation de froid très prononcée de ces tapis, j’ai trouvé d’autres explications. L’une d’elle fait mention d’un gel « activé par la pression ».
Autrement dit, appuyer sur le tapis provoquerait un refroidissement réel du gel qui se trouve dedans : la température du tapis diminuerait quand on appuie dessus.
Ceci est un mécanisme possible : le gel peut être constitué de telle sorte qu’une pression peut lui faire changer son état moléculaire, ou juste son état physique, de façon à entrer dans une phase de plus basse entropie. Ce changement de phase est alors endothermique et la température baisse. D’un point de vue purement conceptuel, c’est quelque chose qui serait possible.
Cependant, en effectuant mes essais sur mon propre tapis, je n’ai pas observé de baisse de température lorsque j’ai posé un poids sur le tapis. Il n’y a donc pas de phénomène endothermique en jeu. En revanche, mon tapis en entier monte en température lorsque je pose mes pieds dessus : c’est donc bien signe que des calories sont rapidement captées de mes pieds et renvoyées dans tout le tapis.
Enfin, si la compression produisait un refroidissement, un relâchement devrait produire un échauffement. C’est obligatoire. Or ce n’est pas le cas et même le contraire : dès que l’on retire la main chaude du tapis, ce dernier n’est plus réchauffé par la main et commence à perdre en température.
Des tapis tirant parti d’un phénomène endothermique peuvent exister, mais mon tapis n’est pas de ce genre-là. Le principe d’un « gel activé par la pression » est donc très probablement un simple « argument » commercial.
Conclusion
Les tapis rafraîchissant ne deviennent pas réellement froids, pas plus que le carrelage de la salle de bain n’est plus froid que le tapis qu’on pose dessus : les deux sont à la même température. La sensation de froid ne provient que du mécanisme qui vole la chaleur de votre pied ; mécanisme bien plus fort avec le carrelage qu’avec un tapis.
Ces mécanismes font intervenir la captation de la chaleur corporelle ainsi que son transport au sein du tapis, et le tout est optimisé par le choix des matériaux pour avoir une sensation de froid agréable en périodes de fortes chaleurs, y compris pour nos animaux de compagnie.
Liens
Si, au lieu de froid, vous voulez plutôt avoir chaud, vous pouvez essayer de voir du côté des chaufferettes, pratiques à mettre dans vos poches. Il en existe qui fonctionne avec des cristaux exothermiques, ou alors les chaufferettes catalytiques qui fonctionnent avec de l’essence à Zippo.
Quelques liens de ressources et de discussions :
- Pressure activated gel cooling pads for dogs: what are the physics behind them?
- How do pet cooling mats work?
- Cooling Gel Pillow. – Keeping It Cool
- How do pet cooling mats work ? : chemistry
Le lien vers mon modèle de tapis rafraîchissant :
- Tapis Rafraîchissant Chien et Chat (lien Amazon)
Pourquoi le mois de juin n’est pas le mois le plus chaud, alors que c’est le mois où les jours sont les plus longs ?
Couleur science par Anonyme le 06/07/2023 à 06:27:00 - Favoriser (lu/non lu)

Si l’on regarde la durée du jour et de la nuit pour les mois de l’année (en France), c’est le mois de juin qui a les jours les plus longs. Si l’on regarde les mois le plus chaud, c’est le plus généralement juillet, et même assez souvent août :
| Mois | Durée moyenne du jour |
|---|---|
| … | … |
| avril | 13h38 |
| mai | 15h10 |
| juin | 15h57 |
| juillet | 15h32 |
| août | 14h10 |
| … | … |
| Année | Juin | Juillet | Août |
|---|---|---|---|
| 2022 | 21,2 | 23,2 | 23,7 |
| 2021 | 20,3 | 20,7 | 20,0 |
| 2020 | 18,6 | 21,6 | 22,6 |
| 2019 | 20,1 | 23,0 | 21,8 |
| 2018 | 20,1 | 23,2 | 22,3 |
| 2017 | 21,2 | 21,7 | 21,5 |
| 2016 | 18,7 | 21,3 | 21,5 |
| 2015 | 19,8 | 22,8 | 21,6 |
| 2014 | 19,6 | 20,6 | 19,1 |
Comment expliquer cette différence ? Pourquoi le moins le plus exposé au Soleil n’est pas le plus chaud ?
Le solstice d’été
Le mois de juin marque le début de l’été, car il contient le jour du solstice d’été.
Le solstice est avant tout un phénomène astronomique. La Terre parcourt son orbite autour du Soleil en une année. L’axe de notre planète étant inclinée par rapport au plan de son orbite — appelé plan de l’écliptique — chaque hémisphère est donc tantôt dirigé au centre de l’orbite, tantôt dirigé vers l’extérieur. Le solstice d’été correspond au moment où l’hémisphère nord de la Terre est dirigé vers le Soleil.
Vu de cet hémisphère, le Soleil est à son point le plus haut dans le ciel ce jour-là.
Cela tombe généralement un 21 juin, mais peut se retrouver entre le 19 et le 22 juin, selon les années. D’un point de vue du calendrier, le jour du solstice est le jour où la journée est la plus longue, et la nuit la plus courte. C’est donc pour cette raison que le mois de juin, et pas un autre, a les jours les plus longs de l’année.
Or, la Terre, en tout cas un hémisphère donné, reçoit sa lumière, sa chaleur et toute son énergie de la part du Soleil et en journée. Si les jours sont plus longs, cet hémisphère reçoit plus d’énergie.
Globalement, le mois de juin est le mois le plus d’heures de Soleil (toujours dans l’hémisphère nord) : il s’agit donc aussi le mois où l’hémisphère nord reçoit le plus d’énergie. Logiquement donc, le mois de juin devrait être le mois le plus chaud. Pourtant, c’est rarement le cas.
Pourquoi un délai entre l’énergie reçue et la température ?
Il est facile de répondre à cette question, mais également très facile de tomber dans le piège de la mauvaise réponse.
Ce piège est de penser que lorsque l’on chauffe un corps pendant une durée donnée, alors sa température est au plus haut au milieu de cette durée.
Ceci est faux. Quand on chauffe un corps, le moment où il est le plus chaud est celui où l’on coupe la chauffe. Ainsi, une casserole que l’on met sur le feu de 12h00 à 12h10 sera donc à son plus chaud à 12h10, et non pas 12h05. Ceci provient du fait que la chaleur s’accumule avec le temps, et donc plus le temps passe, plus on en a, même si on chauffe moins.
Pour ce qui est de l’hémisphère nord chauffé par le Soleil, c’est la même chose. Ainsi, ce n’est pas parce que juin est le mois le plus chauffé par le Soleil que c’est là où la température est le plus élevée.
Au cours d’une année, l’hémisphère Nord reçoit évidemment de l’énergie toute l’année, mais les mois où il en reçoit le plus sont ceux centrés sur juin, donc d’avril à août. On peut dire que c’est notre période de chauffe.
Si on comprend ce que l’on vient de voir, alors on comprend que l’hémisphère est au plus chaud à la fin de cette période, soit juillet ou août.
En juillet et août, les jours sont de plus en plus courts, mais tout comme notre hémisphère reçoit de la chaleur en journée, il en perd la nuit (par rayonnement dans l’espace). Or, en juillet et en août, il en gagne toujours davantage en journée qu’il n’en perd la nuit. Durant ces deux mois, donc, le bilant thermique est donc toujours positif et la chaleur continue de s’accumuler.
Ce n’est généralement qu’à partir de septembre que la baisse de la durée des journées est suffisante, et que la chaleur perdue la nuit est supérieure à la chaleur gagnée le jour, que l’hémisphère finit par refroidir.
Une dissymétrie dans la température globale du sol
Pour savoir quel mois il fait le plus chaud, il faut aussi considérer la température du sol avant le réchauffement estival. En effet, si le sol était particulièrement froid avant, il mettra là aussi plus de temps à gagner en température.
Et c’est exactement ce qui se passe : au printemps (avril et mai, et même juin), l’hémisphère nord sort d’une période où il a fait très froid. La chaleur reçue et accumulée au printemps sert donc avant tout à compenser le froid de l’hiver, et celle de juin, juillet et août permettent ensuite de réellement chauffer.
Un peu comme en cuisine il faut compter quelques minutes pour décongeler un aliment avant de réellement pouvoir commencer à le cuire.
Il est donc bien normal qu’il fasse plus chaud après le mois de juin plutôt qu’avant, même si les mois d’avril et d’août ont à peu près les mêmes temps d’exposition au jour.
La même logique peut d’ailleurs être appliquée en automne et en hiver. En automne, le sol est encore chaud et son inertie thermique acquise en été. Cela permet donc d’avoir de la chaleur de septembre à novembre. Le mois de décembre, qui totalise le moins d’exposition au Soleil, n’est généralement pas le plus froid non plus ; ce titre revenant plutôt à janvier ou à février.
Il y a donc constamment un décalage entre la quantité d’ensoleillement et d’énergie reçue et la courbe de température au cours d’une année, essentiellement à cause de l’inertie thermique du sol.
Enfin, un décalage similaire est observé au cours d’une journée. Bien que le moment où le Soleil tape le plus fort soit 14 h (en France et par définition ; midi + 2 heures), le moment le plus chaud se situe bien après ça, autour de 16 h à 17 h. La raison est identique : le matin, le Soleil compense le froid de la nuit, et ce n’est qu’après que la chaleur sert à vraiment chauffer le sol et l’air. Vous pouvez voir l’article dédié à cette question.
D’où viennent les aurores polaires ?
Couleur science par Anonyme le 01/06/2023 à 05:58:00 - Favoriser (lu/non lu)

On rencontre typiquement les aurores polaires au niveau des pôles de la Terre, mais parfois, ceux-ci peuvent descendre à des latitudes plus basses, y compris de façon exceptionnelle en France métropolitaine.
D’où viennent-elles ? Pourquoi elles donnent ces couleurs ? C’est l’objet de cet article.
Définitions
Bien que l’on parle souvent d’aurores boréales, le terme général est plutôt aurores polaires. Boréale signifie simplement le nord, et les aurores boréales sont donc les seules aurores proches du pôle Nord.
Quand les aurores ont lieu au pôle Sud, on parle des aurores australes.
Quant au terme d’aurore lui-même, il vient du latin aurora, qui signifie briller. Une aurore brille dans le ciel. Le terme désigne également les premières lumières du matin (pour la même raison), et se retrouve aussi dans les racines étymologiques de l’or (aurum, en latin), à nouveau parce que ça brille.
Cela ne nous dit d’où elles viennent quand on les voit dans le ciel.
Origine des aurores
Les aurores sont des phénomènes lumineux provenant de l’interaction entre les molécules de l’atmosphère (azote, oxygène, hydrogène…) et les particules libérées par le Soleil lors des éruptions solaires.
Le Soleil, par son activité thermique et magnétique, souffle en permanence des particules électriquement chargées (protons, électrons) dans toutes les directions. On parle du vent solaire. Il lui arrive d’émettre des bourrasques de particules nettement plus fortes qu’à l’habitude. Cela se produit lorsque l’activité magnétique solaire atteint des pics lors des cycles solaires, tous les 11 ans environ. On parle d’orages magnétiques.
Dans ces cas-là, si la bourrasque se dirige vers la Terre, les particules finissent piégés par le champ magnétique terrestre. Elles sont alors déviées le long des lignes de champ. Or, ces lignes pointent vers les régions polaires, où elles concentrent les particules avant de les envoyer sur la haute atmosphère, entre 80 et 1 000 km environ.
C’est pour cette raison que les aurores sont visibles vers les pôles.
Ce sont ensuite les collisions et les interactions entre ces particules solaires et les particules atmosphériques de la Terre qui produisent de la lumière.
D’où viennent leurs couleurs ? Pourquoi y en a-t-il des différentes ?
L’interaction qui a lieu entre les particules chargées du Soleil et l’atmosphère résulte en une excitation des atomes de l’atmosphère. Lorsque les atomes se désexcitent, cela se traduit par la libération d’un photon de lumière.
Chaque gaz produit ainsi son propre spectre de couleurs en réaction à une excitation extérieure.
C’est le principe des enseignes lumineuses en vogue des années 1950-1960, et faites de tubes néon : le néon produit une couleur orange vif en cas d’excitation, alors que l’hélium produit plutôt du blanc, et le xénon du bleu :

La même chose s’observe dans l’atmosphère. Dans l’atmosphère, on a principalement de l’oxygène (21 %) et de l’azote (78 %). Le reste, moins de 1 % restant, correspond à d’autres gaz (argon, dioxyde de carbone, eau…). Ces gaz sont relativement bien mélangés au niveau sol, mais ce n’est pas forcément le cas en altitude : là, la vitesse thermique des molécules font qu’à certaines altitudes on trouve préférentiellement certains gaz et pas d’autres.
Par conséquent, quand les particules solaires arrivent dans l’atmosphère, en fonction du type de choc (élastique, inélastique…), de la vitesse de l’impact et de la molécule heurtée, la réaction n’est pas la même et la lumière émise lors de la désexcitation est différente également.
Ainsi, quand ces interactions ont lieu entre 120 et 180 km, on observe des lumières vertes et rouges à cause de l’oxygène. Quand les interactions ont lieu à plus basses altitudes, l’azote est majoritaire dans l’atmosphère et l’on observe du bleu, rouge et violet.
Tout ceci doit évidemment également se produire la nuit (sinon la lumière du jour masque le phénomène), et lorsque le ciel est dégagé de nuages. Les projections de particules solaires doivent aussi évidemment être faites en direction de la Terre. Cela fait beaucoup de conditions à réunir et l’ensemble reste donc un phénomène assez rare et spectaculaire.
Quelles conséquences pour nous ?
Les aurores, les phénomènes lumineux n’ont pas de conséquences directes sur nous, si ce n’est qu’elles sont jolies, fascinantes et qu’on aime les regarder. Certaines cultures y associent également des croyances : au Japon par exemple, voir des aurores est le signe d’un mariage heureux.
Ce qui peut avoir une conséquence, ce sont les phénomènes qui donnent naissance aux aurores : les vents solaires. Rappelons que ce sont des particules chargées, et donc d’énormes courants électriques. Ces courants produisent des champs magnétiques qui à leur tour vont induire des surtensions dans toutes les structures conductrices sur Terre, et en particulier dans les lignes haute tension longues distances, provoquant des incidents électriques et des coupures. Ce fut le cas par exemple en 1989 au Canada et aux USA, où 6 millions de personnes furent plongés dans le noir durant plusieurs heures.
Le bombardement de particules chargées lui-même peut affecter ou endommager l’électronique parfois fragile, surtout quand ce dernier est utilisé en altitude (avion, montagne) en raison d’une moins grande épaisseur d’atmosphère protectrice.
Les cartes électroniques des satellites ou des sondes spatiales sont d’ailleurs plus robustes et résistantes à tout ça : la gravure des circuits intégrés y est beaucoup moins fine.
Références et liens
Comment fonctionnent les billes déshumidifiant en silicates ?
Couleur science par Anonyme le 04/05/2023 à 06:33:00 - Favoriser (lu/non lu)

Dans la vie courante, vous avez sûrement déjà rencontré des petits sachets de dessicant en gel de silicates, aussi appelé silicate synthétique amorphe. On en trouve dans les boîtes de chaussures neuves ou les poches des vêtements dans les magasins, par exemple, mais ses applications vont bien au-delà de ça.
Ils servent à déshumidifier et éviter que l’humidité ambiante ne détruise la marchandise.
Comment ça marche ?
Ces billes de silicates (oxydes et hydroxydes de silicium) sont dures et ne prennent pas forcément de volume lorsqu’ils adsorbent l’humidité. Contrairement à une éponge, ils ne deviennent pas non plus humides au toucher. Leur principe « actif » peut donc sembler un peu mystérieux, surtout si l’on compare aux billes en polymère super-absorbants (« jelly-marble »), qui elles prennent jusqu’à 100 fois leur volume et qui sont humides au toucher.
Les billes en gel de silice sont des silicates, donc essentiellement une structure minérale en dioxyde de silicium. Il s’agit de la même composition chimique que le quartz ou le verre de la vie courante, voire tout simplement du sable. Ce qui change est essentiellement la disposition des molécules, plutôt que la composition.
La particularité du gel de silicate est qu’il est préparé de façon à avoir une structure nano-poreuse. La composition chimique est identique, c’est juste l’agencement mécanique qui diffère.
En l’occurrence, la structure de ce « gel » — qui est tout de même dur et non réellement gélatineux — se présente comme un amas de « globules » de dioxyde de silicium entre lesquels se situent des pores. C’est donc une structure aérée, peu dense. Ce sont ces pores qui adsorbent les molécules d’eau et piègent l’humidité :
Notez bien que l’on parle ici d’adsorption — avec un D — et pas d’absorption, avec un B. La différence est importante.
L’adsorption est un phénomène de surface : les molécules adsorbées se fixent sur la surface de la matière adsorbante, éventuellement sous la forme de plusieurs couches successives, alors que pour l’absorption, le produit absorbé finit dans le volume de la structure absorbante et peut participer à sa cohésion.
Dans ces conditions, si l’on veut que l’eau soit adsorbée en grande quantité, il faut une surface importante. L’efficacité du dioxyde de silicium préparé sous forme de gel de silice en tant que dessicant réside dans sa très grande surface spécifique. C’est le rôle de ces globules et des pores : chaque globule présente une surface qui permet l’adsorption, là où une structure pleine ne présenterait aucune surface utile à l’intérieur.
Le gel de silice présente de cette façon une surface active de l’ordre de 750 à 800 m² par gramme !
On retrouve ce principe dans le charbon végétal (charbon actif) également, qui possède lui aussi une très grande surface spécifique sur lequel peuvent se fixer des impuretés diverses (raison pour laquelle on utilise le charbon végétal comme filtre pour capturer les odeurs et autres molécules étrangères).
Le gel de silice présente lui une grande affinité avec les molécules polaires, typiquement l’eau. Les molécules d’eau qui arrivent en contact avec la surface, finissent piégées par le gel et ne se retrouvent alors plus dans l’air, d’où ses propriétés dessicants.
Que se passe-t-il si l’on mange ces billes ?
En un mot : rien.
Bien que l’on mette ces billes dans des sachets où l’on indique « ne pas avaler » ou « do not eat », le gel de silice reste non toxique, non combustible et non dangereux : il ne s’agit que de sable capable d’adsorber un peu d’eau.
Leur pouvoir d’adsorption reste limité en fonction du volume de gel de silice, ce n’est donc pas non plus ça qui va vous déshydrater de l’intérieur.
Le produit est simplement mis dans un sachet « ne pas manger » car ce n’est pas pour autant comestible. Il s’agit aussi d’éviter toute confusion avec des sachets de condiments, sel ou poivre, que l’on peut trouver dans les restaurants par exemple.
Et les billes bleues ?
Il existe des billes de silices bleues, ou même roses, oranges. Ce sont des billes identiques mais dans lesquelles on a ajouté un colorant dont la couleur est visible quand la bille a adsorbé de l’eau. Dans ce cas, son pouvoir dessicant est terminé et il n’aide plus à assécher l’air. La présence du colorant aide alors à savoir si le dessicant doit être renouvelé ou réactivé.
Historiquement, on utilisait du chlorure de cobalt pour ça : les billes passaient alors de bleu (sec) à rose (hydraté). Il n’est plus utilisé aujourd’hui, car ce produit est toxique voire cancérigène.
Parmi les colorants utilisés aujourd’hui, on peut citer le sulfate d’ammonium et de fer, qui est orange quand il est sec mais incolore ou blanc lorsqu’il est hydraté.
Lorsque l’on détecte que le dessicant est hydraté, il convient alors de le réactiver par un passage dans un four par exemple, pour faire sortir l’humidité et les rendre dessicant de nouveau.
Le gel de silice seul (sans colorant) est non toxique, non réactif et sous sa forme de petites billes ne constitue pas de réel danger. Les billes cassées peuvent cependant engendrer des poussières irritantes.
Ressources
Matière noire, énergie noire et courant noir
Couleur science par Anonyme le 06/04/2023 à 06:59:00 - Favoriser (lu/non lu)

Le tableau périodique compte 118 éléments chimiques connus, pourtant, tout cela n’explique que 5 % l’univers.
Tout ce que l’on voit, les galaxies et les étoiles, les planètes, les animaux et les plantes, les océans et les montagnes, nos machines et nos outils, aussi diverses qu’elles soient, sont faits des éléments du tableau périodique, qui sont la matière baryonique et qui ne correspond qu’à 5 % de l’univers.
Sur ce pourcentage, et à l’échelle de l’univers, 90 % de tout ça n’est que de l’hydrogène. C’est-à-dire un simple proton associé (ou pas) à un simple électron, produits suite au big-bang et subsistant depuis, amassés en étoiles (où d’ailleurs l’électron est dissocié de son proton). Les 10 % restants sont partagés entre de l’hélium seul d’une part, produit par la fusion de l’hydrogène dans les étoiles et les autres éléments d’autre part (oxygène, silicium, carbone, fer, or, uranium, magnésium…) qui ensembles ne constituent qu’une infime fraction des atomes de l’univers.
Un rocher, ou même la planète Terre tout entière, aussi grande qu’elle nous apparaît, n’est donc constitué que d’éléments à l’état de trace dans la composition de l’univers. Vous vous sentez insignifiant ? Ce n’est pas terminé.
Que compose donc les 95 % restants de l’univers ? Pourquoi ne la voit-on pas ?
Imaginez-vous marcher sur la plage ou dans la neige et apercevoir des empreintes de pas. Qui les a laissés là ? On ne sait pas : il n’y a personne aux alentours. Pourtant les traces sont là. Quelqu’un a dû les laisser, c’est une certitude.
Dans le cas de ces 95 % de l’univers, c’est la même chose. Bien qu’on ne les voie pas, et qu’on ne sait pas ce que c’est, on voit les traces qu’elles laissent dans l’univers.
Mieux, on a découvert qu’il y a deux types d’empreintes : une gravitationnelle et une liée à l’expansion de l’univers. On a donné, à ces deux choses le nom de matière noire et énergie noire (ou sombre). Ces deux choses ne sont pas à confondre avec l’antimatière, qui est encore autre chose, et qui fait partie de la matière baryonique normale.
On peut aussi citer le courant noir, un autre phénomène mystérieux et d’origine inconnu.
La matière noire
La première correspond à environ 25 % de ce que compose l’univers, et représente donc cinq fois plus que la matière normale. Elle a été découverte en analysant la vitesse de déplacement de galaxies au sein d’amas de galaxies, dès 1933, puis redécouverte près de quarante années plus tard.
Dans un amas de galaxies, toutes les galaxies orbitent le même centre de masse, et normalement, les galaxies proches du centre se déplacent bien plus rapidement que celles plus éloignées. La diminution de la vitesse en fonction de la distance suit une loi bien précise et parfaitement connue. Or, on a constaté que cette règle n’était pas respectée pour les galaxies dans ces amas, ni même pour les étoiles dans une galaxie.
Une des façons d’expliquer ça, fut par l’hypothèse d’une masse cachée, invisible. On a baptisé ça la « matière noire ». On ne sait vraiment pas grand-chose à son sujet, mais on sait :
- que c’est là, ou en tout cas que quelque chose est là ;
- que ça agit au travers de l’interaction gravitationnelle ;
- qu’il y en a environ 5 fois plus que de matière normale.
Et… c’est à peu près tout à ce jour. La nature exacte reste un mystère à ce jour.
La matière noire n’est pas visible, elle n’interagit donc pas avec la force électromagnétique. Elle ne forme pas de « molécules » et semble ne pas former d’astres denses. Elle semble juste constituer de larges amas autour des galaxies.
L’hypothèse d’une masse fantôme 5 fois plus grande que la matière ordinaire expliquerait d’autres phénomènes étonnants dans l’univers et l’espace, comme les variations dans le fond diffus cosmologique. Ce dernier est la chaleur rémanente du Big-Bang, qui est globalement homogène dans l’univers tout comme la distribution des galaxies dans la galaxie.
Les seules variations ne sont que de ±0,1 % par endroit : c’est faible, mais elles restent anomalistiques. Néanmoins, les différentes simulations numériques arrivent à les retrouver, à condition d’avoir un univers cinq fois plus massif que ce qu’on a avec la seule matière visible.
On a donc des preuves suffisantes pour dire qu’il existe quelque chose. Quant à savoir si c’est vraiment une masse, ou une « matière », rien n’est moins sûr. Il existe d’autres hypothèses concurrentes.
La plus connue est probablement la théorie MOND (MOdified Newtonnian Dynamics), qui se destine à expliquer les mouvements des galaxies et l’anomalie du fond diffus cosmologique par une modification de la mécanique newtonienne. Elle semble moins soutenue que celle d’une vraie « matière » fantôme.
Une autre voudrait que la masse manquante soit le résultat de l’interaction de notre univers avec un autre univers, et qui agirait dessus à distance, à la manière d’un aimant caché sous une table qui agit sur un trombone posé dessus.
Certains pensent que la matière noire est juste de la matière « normale » mais que l’on ne verrait pas : petits trous noirs, ou particules très légères mais hyper-nombreuses, telles que des neutrinos (regroupées sous le terme de WIMPs : weakly interacting massive particles), des formations inconnues composées de particules connues (strangelet, ou particules formés de multiples quarks). D’autres penchent pour une cinquième force fondamentale, une anomalie dans la supersymétrie, etc.
Mais à cause de l’absence de preuves directes, cela fait 90 ans que le mystère reste entier, malgré des dizaines d’expériences scientifiques. Les premiers résultats de détection d’ondes gravitationnelles encouragent à penser qu’on a enfin une méthode pour analyser la matière noire qui n’agit que par gravité, mais on est encore dans un épais brouillard scientifique tout de même.
L’énergie noire
L’énergie noire, elle, est tout à fait autre chose. Son hypothèse est également plus récente et remonte à 1997 !
En relativité générale, les équations permettent tout un tas de choses que la physique classique ne permettait pas. L’une de ces choses est un univers en expansion. Ceci a été mis en évidence par Edwin Hubble, le scientifique éponyme du télescope. Ce dernier remarqua que les galaxies lointaines subissaient davantage le phénomène de décalage vers le rouge — le redshift — que les galaxies plus proches. Cela signifiait que les galaxies lointaines s’éloignaient plus vite.
L’explication à ça est que l’univers était en expansion et que plus les galaxies étaient distantes de nous, plus il y a d’espace qui s’étire, et donc plus l’expansion les éloigne de nous. La lumière émise par ces galaxies étant elle aussi étirée, les longueurs d’ondes s’en voient d’autant plus allongées que les galaxies sont loin.
Or, si notre univers grandit à chaque seconde qui passe, ça signifie que par le passé, il était plus petit. Aussi, si l’on remonte assez en arrière, il y a un moment où sa taille devait être nulle. Cette idée — nouvelle en 1930 — était considérée comme ridicule et on donna ironiquement le nom de « big bang » à l’explosion qui provoqua l’expansion initialement.
Pourtant, beaucoup d’indices incontestables aujourd’hui montrent que notre univers est bien en expansion.
Une question qui vient dès lors est de se demander si cette expansion ralentit ou non, et donc de savoir s’il arrivera un moment où l’univers cesse de s’étendre pour amorcer une contraction (et éventuellement un retour vers un état ultra-dense, c’est-à-dire l’idée connue sous le nom de « big crunch »), puis une explosion de type big-bang de nouveau, créant un processus cyclique sur la formation de notre univers.
Les mesures qui suivirent pour répondre à cette question donnèrent un résultat inattendu : non seulement l’expansion ne ralentit pas, mais en plus elle accélère ! Ceci semble enfreindre tout un tas de lois physiques, mais c’est ce qu’on observe.
Le taux d’expansion est connu sous le nom de constante de Hubble. On mesure ainsi que l’univers gonfle de 70 km/s par mégaparsec. Ça signifie qu’une galaxie située à 1 mégaparsec (3 261 564 années lumière) s’éloigne de nous, et nous d’elle, avec une vitesse de 70 km/s. C’est donc cette vitesse qui croît avec le temps.
Bien-sûr, si l’univers gonfle de plus en plus vite, une certaine pression ou énergie le pousse à faire ça. Mais laquelle ? Cette « énergie » inconnue, c’est l’énergie noire.
Tout comme pour la matière noire donc, on ne sait pas grand-chose à son propos. On sait seulement qu’elle est là, quels sont ses effets et aussi qu’elle est sans cesse créée. En effet, si l’univers gonfle, l’énergie doit logiquement être de plus en plus diluée et donc de moins en moins active. Or c’est l’inverse que l’on observe ! L’énergie noire est donc de plus en plus active, donc si elle était créée constamment. À partir de quoi ? On ne sait pas. Une hypothèse serait qu’il s’agit d’une propriété intrinsèque de l’espace. Et comme l’espace s’étend, l’énergie noire est de plus en plus importante aussi.
Si l’énergie sombre se crée de nulle part aujourd’hui, c’est qu’il y en aura de plus en plus avec le temps qui passe, mais aussi qu’il y en avait de moins en moins si l’on remonte le temps. En particulier, juste après le Big Bang, il y en avait moins que la matière (et la matière noire). La gravité agissant de façon attractive sur la matière, en l’absence d’énergie sombre suffisante, l’expansion doit ralentir. Ceci s’est bien produit durant environ 8 milliards d’années, mais depuis 5 milliards d’années après, l’expansion est en accélération.
Cela semble enfreindre les lois les plus fondamentales de la physique, mais ça ne semble pas plus absurde que l’idée d’un univers tout entier lui-même né d’une explosion originelle ! Ainsi, si l’on peut accepter l’idée d’un big-bang sorti de nulle part, il devrait être acceptable l’existence d’une énergie dont il s’en crée également de plus en plus à mesure que l’espace grandit.
Les raisons ou l’origine de tout ça demeurent un mystère, mais on estime que la quantité « d’énergie » qui pousse notre univers à gonfler de plus en plus vite est aujourd’hui telle que ça représenterait environ 70 % de tout ce qu’il contient.
On peut digresser un peu et imaginer ce qui va se passer dans l’avenir, si l’expansion augmente de plus en plus.
La constante de Hubble nous dit qu’un objet situé à 1 mégaparsec s’éloigne de nous à 70 km/s. S’il est situé à 2 parsecs, il s’éloigne de nous à 140 km/s. Logiquement, un objet suffisamment éloigné pourrait s’éloigner à une vitesse dépassant la vitesse de la lumière. Ce n’est pas tant son éloignement qui a cette vitesse, mais plutôt la « création » de distance entre nous et l’objet. Dans les deux cas, le résultat est le même : de la lumière émise par cet objet ne pourra jamais nous atteindre, car l’expansion sera plus rapide que le déplacement de la lumière.
Il existe donc une distance au-delà de laquelle aucune information ne peut nous parvenir : on appelle ça l’horizon cosmologique.
Si cette expansion s’accélère avec le temps, la constante de Hubble grandit et l’horizon cosmologique se rapproche. Il arrivera un moment où l’horizon cosmologique sera de plus en plus proche de nous. Les galaxies lointaines finiront au-delà et des galaxies visibles aujourd’hui s’éteindront peu à peu, et disparaitront de notre connaissance.
Si l’expansion s’accélère encore, l’horizon cosmologique peut se rapprocher indéfiniment. Assez en fait, pour séparer même les atomes et particules. Dans ces conditions, toutes les particules, tous les atomes finiront par s’éloigner de toutes les autres à des vitesses supraluminiques. Il n’y aura alors plus aucune interaction entre les particules et l’univers sera à un stade de mort thermodynamique.
Le courant noir
Tout comme la matière noire et l’énergie noire, le qualificatif de « noir » désigne davantage quelque chose que l’on ne voit pas, que quelque chose de couleur noire.
Pour celui-ci, il n’y a pas de consensus scientifique. Il est néanmoins assez mystérieux de noter et d’étudier quelques étonnements obtenus dans divers travaux de recherches, en particulier quand cela concerne un éloignement mystérieux et uniforme d’une partie de l’univers à 600 kilomètres par seconde…
Si l’on n’avait que l’expansion uniforme de l’univers, alors toutes les galaxies situées à la même distance de nous s’éloigneraient à la même vitesse quelle que soit la direction dans laquelle on regarde. Or, des observations menées dès 1973 montraient que d’un côté de nous les galaxies s’éloignent plus vite que de l’autre côté. Dans un référentiel plus englobant, cela voudrait dire que les galaxies dans leur ensemble ont un déplacement global net vers une direction en particulier. C’est ce déplacement unidirectionnel d’un paquet de galaxies que l’on appelle le courant noir, ou flux noir, si on traduit ça de l’anglais dark flow.
Si le courant noir est un déplacement des galaxies vers un endroit en particulier, on peut se demande quelle source attractive — a priori gravitationnellement — provoque ça.
Diverses études (2008, 2013) depuis ces observations semblent tantôt mettre en doute le courant noir, tantôt nous conforter dans l’hypothèse de son existence. Le problème réside essentiellement dans le fait que les infimes hétérogénéités dans l’intensité du fond diffus cosmologique et la distribution de masse dans l’univers visible ne peuvent expliquer totalement ce que l’on voit. On n’a donc aucune conclusion exacte à donner dans la cause de ces observations.
Le Grand Attracteur, une concentration de galaxies au sein de notre superamas de galaxies Laniakea et situé environ 200 millions d’années lumière de nous (ce qui n’est pas énorme à l’échelle de l’univers visible) et d’une masse de 150 000 galaxies (2×10¹⁶ masses solaire) semble ne pas être la cause du courant noir : les effets du courant noir s’étendraient en effet beaucoup plus loin, à des distances comptées en milliards d’années lumières…
Une hypothèse est que le déplacement actuel soit le déplacement rémanent provoqué par l’attraction de quelque chose situé au-delà de l’horizon cosmologique, et que nous ne pouvons pas voir aujourd’hui, ni visuellement avec la lumière, ni par gravité (ces deux phénomènes se déplaçant à la vitesse de la lumière, rappelons-le).
En conclusion
Cet article présente deux phénomènes (voire trois si on inclue le courant noir dont on n’est pas encore sûr) dont le processus demeure, aujourd’hui encore, inconnu.
On observe des choses, parfois avérées, mais on ne sait pas encore les expliquer.
Ici, on sait que l’on ne sait pas, ce qui est déjà pas mal : on aurait également pu ne pas savoir que l’on ne savait pas. Il y a donc des choses que l’on sait inconnues, et d’autres, probablement encore plus nombreuses dont on ignore jusqu’à l’existence.
La recherche est là pour lever les doutes et les interrogations. Il s’agit d’un processus long et complexe, mais qui avance petit à petit malgré tout. Et plus la recherche avance, plus la somme de ce que l’on sait et connaît augmente et plus l’on progresse dans ce brouillard épais des connaissances.
En sciences toujours, l faut mieux admettre que l’on ne connaît pas quelque chose (et éventuellement stimuler les recherches sur le sujet), que s’inventer des conclusions et des raisons sorties de l’imaginaire et produites sans preuve, ou même d’indices.
En sciences, ne pas savoir n’est pas un problème.
- Dark Flow & The Great Attractor - YouTube
- What is Dark Matter and Dark Energy? - YouTube
- The Absurd Search For Dark Matter - YouTube
- Dark Flow & The Great Attractor - YouTube
- Cosmological constant — Wikipedia
- Where Did Dark Matter And Dark Energy Come From?
- Grand attracteur — Wikipédia
- NASA - Mysterious Cosmic 'Dark Flow' Tracked Deeper into Universe|https://www.nasa.gov/centers/goddard/news/releases/2010/10-023.html]
Image d'en-tête de Don Mc Crady
Comment fonctionne un silencieux de pistolet ?
Couleur science par Anonyme le 16/03/2023 à 05:29:00 - Favoriser (lu/non lu)

On connaît tous très bien les films de James Bond où un tireur utiliser une arme à feu avec un silencieux : tirer avec l’arme transforme le bruit du coup de feu en un simple « clic » dû simplement bruit mécanique lié à la détente et au percuteur. Sauf que, bien-sûr, ceci est totalement idéalisé.
Dans le monde réel, le silencieux est très loin d’être « silencieux » : au mieux, le bruit passe de clairement assourdissant à juste très fort (termes scientifiques… ou pas), mais le coup de feu est toujours là. Le terme de « silencieux » est d’ailleurs plutôt un terme grand public : plus techniquement on parle généralement de modérateur de son, ou encore de suppresseur (de l’anglais « suppressor »).
Il y a pourtant tout de même une nette amélioration, et elle est plus utile au tireur afin de protéger son ouïe, plutôt que réellement tuer quelqu’un sans se faire entendre.
La science et l’ingénierie derrière tout ça reste assez intéressante et c’est donc pour ça que cet article a été écrit.
Du bruit d’un coup de feu
Pour savoir comment fonctionne un silencieux, il faut d’abord connaître le mécanisme derrière le coup de feu, pourquoi c’est si bruyant, et ensuite trouver des moyens pour réduire ces effets-là.
Il y a essentiellement deux choses qui font du bruit quand on tire avec une arme :
- le coup de feu lui-même, à cause de l’explosion de la charge de poudre ;
- le crack supersonique, correspondant à la balle qui traverse l’air à une vitesse supersonique.
On va commencer par le crack supersonique. C’est la même chose qu’un bang supersonique d’un avion : la balle, comme l’avion, traverse l’air à une vitesse supérieure à la vitesse du son dans l’air. Ce qui arrive alors, c’est que les ondes sonores, qui s’échappent de la balle sont rattrapées par la balle elle-même. Les nouvelles ondes produites sont donc produites les unes par-dessus les autres :

Il se forme alors un cône, appelé cône de Mach, où les compressions-décompressions qui constituent l’onde sonore se superposent et forment donc une zone de compression-dépression très importante, autrement dit, un son très intense, correspondant à un « bang ».
Même un petit projectile peut ainsi produire un bang assez fort et très bien audible, surtout quand on se trouve à proximité de la trajectoire de la balle.
Ce bruit-là est lié au déplacement de la balle elle-même, et un silencieux que le supprimera pas. On peut cependant utiliser une munition moins chargée en poudre : la balle sera alors tirée avec moins de puissance et donc moins vite. On parle de munitions subsoniques. L’onde de compression-décompression ne s’accumulera plus devant la balle et ne produira plus le fameux bang.
Ensuite vient le bruit du coup de feu lui-même. Ce bruit, comme tous les bruits en fait, provient aussi d’une compression-décompression rapide dans l’air. Ici, ce sont les gaz produits par la combustion de la charge qui, lorsqu’elles se détendent brutalement à la sortie du canon, produisent une compression subite de l’air, et à nouveau un son très important. Ces gaz sont à une pression très élevée, de l’ordre de 200 atmosphères.
Précisons que les gaz sont ce qui propulse la balle à leur très haute vitesse : ils sont donc situés dans le dos de la balle et sortent toujours après celle-ci du canon.
C’est sur ce bruit-là qu’un silencieux agit.
Le mécanisme d’un silencieux
Un silencieux est essentiellement une cavité placée au bout du canon d’une arme et qui, à défaut de supprimer totalement le bruit, le réduit tout de même de 20 à 35 dB, ce qui est tout de même assez remarquable, quand on se souvient que l’échelle des décibels est logarithmique.
D’après ce qui précède, pour éviter le bruit, il faut réduire la pression du gaz en sortie du canon, et faire en sorte qu’il sorte beaucoup plus lentement, de façon moins explosive, en somme. Et c’est exactement ce qu’il fait.
Dans un premier temps, le silencieux agit comme une cavité qui recueille les gaz de combustion et leur offre un « espace de détente ». La détente des gaz n’a donc pas lieue dans l’air, mais dans une cavité rigide. Le son ne sort donc (presque) pas dans l’air environnement et il n’y a (presque) pas de bruit.
Aussi, si le silencieux est froid, les gaz de propulsion vont pouvoir se refroidir un peu et ceci réduit également déjà la pression.
Ceci dit, contenir les gaz de combustion ne suffit pas. Le silencieux est toujours rempli des gaz de combustion qui n’étaient pas là avant : il y a donc toujours une surpression et ces gaz doivent être libérées. Pour éviter que cela fasse tout de même du bruit, il faut que la libération du gaz se fasse de façon progressive.
Ici, c’est la géométrie interne du silencieux qui va jouer : leur structure est telle qu’elle forme de multiples cavités et forment même des voies d’évacuations qui empêchent le flux d’air de se faire de façon optimale, et donc de façon ralentie. On retrouve ici le principe d’une valve de Tesla.

Les gaz finissent tout de même par sortir, mais la pression n’est alors que d’environ 4 bars. C’est toujours relativement fort. C’est toujours le double de la pression d’un pneu de voiture, mais tout de même bien moins que les 20 bars de la pression régnant dans une bouteille de champagne. On a donc toujours une compression de l’air en sortie, mais celui-ci est très amoindri.
Conclusion
Contrairement à ce que prétend Hollywood, le silencieux n’est pas totalement « silencieux », loin de là même. Il permet toutefois de réduire le bruit d’un coup de feu d’environ 20 à 35 dB ce qui est représente une division par 30 de l’intensité acoustique.
On obtient ce résultat essentiellement en agissant sur la cause de l’onde de choc d’un coup de feu. Cette onde de choc apparaît suite à une rapide détente de gaz en sortie du canon. En diminuant la vitesse de détente de ces gaz, on réduit le bruit. Le silencieux agit comme une cavité de retenue des gaz en expansion et sa géométrie interne fait tout pour que les gaz s’échappent progressivement.
Ce genre de principe est également utilisé dans les pots d’échappements des véhicules à moteur : chaque explosion dans le moteur produit des gaz dont l’expulsion, très rapide, produit une surpression et donc un son très fort. L’intérieur du pot d’échappement est molletonné et absorbe ainsi l’onde de choc et permet une libération progressive des gaz en sortie
Notons que d’autres méthodes de suppression de bruit existent, comme ceux utilisés pour un casque anti-bruit (avec réduction active) ou dans les aspirateurs et les carburateurs (avec un résonateur de Helmholtz).
Ressources
Quelques expériences avec un aimant
Couleur science par Anonyme le 02/03/2023 à 05:01:00 - Favoriser (lu/non lu)

Dans ce troisième article sur les choses que l’on peut faire à la maison, je vous propose de vous munir d’un aimant puissant (ceux qu’on trouve dans les disques durs par exemple, ou un capable de lever une boule de pétanque).
Repousser de l’eau
Un aimant attire le fer, l’acier et un autre aimant. Concernant le dernier, il peut également le repousser si on change son orientation.
Mais savez-vous qu’il existe également des matériaux naturellement et constamment repoussés par les aimants ? Ce sont les matériaux diamagnétiques.
En présence d’un champ magnétique, les matériaux diamagnétiques développent leur propre champ magnétique, opposé au premier.
Un tel matériau n’est pas magnétique en soi : il n’attire pas le fer et ne repousse pas d’autres matériaux. Mais il repousse un aimant quand ce dernier est suffisamment proche.
L’eau est un matériau diamagnétique, et on peut le voir avec un aimant suffisamment petit et puissant : quand on suspend un aimant au-dessus de l’eau, un petit creux apparaît à la surface du liquide :

Ces expériences où l’on vous montre que les céréales sont attirées par un aimant ne montrent en réalité que le diamagnétisme de l’eau qui compose le lait : l’aimant repousse l’eau, et cela crée un creux à la surface. La céréale tombe alors dans le creux, donnant l’apparence qu’il est attiré par l’aimant.
Cela ne vient pas du fer qui se trouve dans la céréale : l’expérience fonctionne avec du polystyrène ou du pollen, qui ne contiennent pas de fer du tout. D’autres matériaux sont diamagnétiques également, comme le carbone pyrolithique ou le bismuth. Il existe ainsi des figurines où un petit aimant flotte indéfiniment entre deux plaques de bismuth.
Tomber au ralenti
Lorsque l’on fait tomber un objet, il tombe en accélérant à un taux égal à 1 g, où g est l’accélération de la pesanteur), soit 9,81 m/s². Cela veut dire que chaque seconde, la vitesse de chute augmente de 9,81 m/s, ignorant les effets dus aux frottements de l’air.
Maintenant, quand on fait tomber un aimant à travers un tube métallique non-ferreux, même si l’aimant ne frotte pas contre les parois du tube, il est ralenti : l’aimant tombe lentement à travers le tube, défiant alors la gravité.
Il existe deux petits fidgets qui utilisent ce principe pour fonctionner : le Moondrop et le Feel-flux :

Comment ça se fait ?
L’aimant possède un champ magnétique autour de lui. Si l’aimant est immobile, le champ magnétique est statique, invariant. Si l’on bouge l’aimant, alors le champ se déplace avec lui. Autrement dit, si l’on reste posé à un endroit donné, le champ se déplace et varie. Or, un champ magnétique qui varie, ça produit un courant électrique s’il y a un métal pas loin.
C’est ce qui se passe dans le tube : si l’aimant tombe à travers le tube il va induire un courant électrique circulaire dans le tube : on parle de courants de Foucault. Maintenant, que fait un courant électrique ? Il produit un champ magnétique !
Or, le champ magnétique produit par le courant induit par la chute de l’aimant est opposé au champ magnétique de l’aimant lui-même (loi de Lenz). Il en résulte que l’aimant qui chute va voir une force magnétique s’opposer à sa chute : cette force freine la chute de l’aimant et ce dernier tombe au ralenti.
L’aimant ne peut cependant pas s’arrêter totalement : si cela devait arriver, le champ magnétique ne varierait plus, il n’y aurait plus de courant et donc plus non plus de champ magnétique secondaire pour empêcher l’aimant de tomber. En somme, l’aimant est ralenti seulement quand il tombe. S’il s’arrête, on ne peut plus dire qu’il tombe et il n’est plus ralenti.
L’aimant doit tomber pour être ralenti. Et plus l’aimant est puissant, ou plus le tube est conducteur, plus le ralentissement est prononcé : la force empêchant l’aimant de tomber tend alors à s’approche de la force poids qui tire l’aimant vers le bas.
Avec le fidget du Feel-Flux, vous avez la version en cuivre et celle en aluminium. La version en aluminium est bien moins chère, mais celle en cuivre offre un meilleur résultat : le cuivre est meilleur conducteur que l’aluminium.
Enfin, il est à noter que si la chute est ralentie, il y a une déperdition d’énergie cinétique. Cette déperdition a lieu sous forme de pertes thermiques dans le métal. Certains trains ou camions utilisent des freins magnétiques basés sur ce principe pour ralentir sans utiliser de frottements mécaniques (et donc réduit les points d’usure).
Déformer l’image d’un écran CRT
Les écrans CRT, pour cathode ray tube, ou « tubes à rayons cathodiques » sont les écrans cathodiques, ceux des vieilles télés ou écrans.
Ces écrans fonctionnent à base de hautes tensions : une électrode — la cathode — est mise à un très fort potentiel électrique qui va accumuler beaucoup d’électrons dessus. Cette accumulation d’électrons va rendre la cathode très fortement négative et les électrons vont finir par s’en échapper à très grande vitesse, créant un rayon d’électrons.
Vu que le tube cathodique lui-même est sous vide, les électrons fusent à travers le tube à une fraction notable de la vitesse de la lumière. Ils viennent ensuite heurter la surface de l’écran. Ce dernier est recouvert de luminophores et la zone bombardée d’électrons devient lumineuse.
En contrôlant l’orientation du faisceau d’électrons, on arrive à viser les bons pixels et à reconstituer l’image sur la télé.
Les vieux écrans, avant les écrans plats, fonctionnaient comme ça. En soi, c’étaient des accélérateurs de particules de salon.
Maintenant l’aimant : les électrons sont des charges électriques. Or une charge électrique qui se déplace produit un champ magnétique. Si on approche un aimant, le champ magnétique du faisceau va être dévié.
Résultat, si l’on approche un aimant d’un écran cathodique : les électrons tapent dans les mauvais pixels et l’image est déformée. S’il vous reste un tel écran, essayez avec un aimant : cela forme des figures colorées et géométriques, qui tendent à mettre en évidence le champ magnétique de l’aimant (sa forme, son sens…) :

Ces écrans avaient d’ailleurs parfois un bouton « démagnétiser », pour recalibrer l’image et la débarrasser de tout magnétisme résiduel, et ainsi remettre le faisceau en face des pixels.
Ressentir l’oscillation des courants alternatifs
Les aimants sont sensibles aux champs magnétiques : ils réagissent aux champs externes. Ces champs externes peuvent venir d’un autre aimant ou d’un électroaimant. Les transformateurs électriques permettent de convertir de passer d’un courant haute tension (et basse intensité) à un courant basse tension (et haute intensité) en faisant transiter l’énergie électrique par une phase où l’énergie est sous forme magnétique.
Une petite partie de cette énergie magnétique peut fuiter en dehors du bloc transformateur et on peut la détecter. Si l’on tient un aimant dans la main et que l’on approche un dispositif transformateur d’électricité, alors l’aimant se met à vibrer au rythme du champ magnétique dans le transformateur ; lui-même oscillant au rythme des oscillations du courant, généralement 50 Hz.
On peut en faire l’expérience à la maison : les transformateurs électriques ne manquent pas dans nos maisons. Des blocs transformateurs d’un PC, au chargeur d’un téléphone, ou alors, là où ça marche le mieux, ce sont les lampes de bureau basse tension avec un socle. On peut alors poser l’aimant dessus et l’entendre ou le sentir vibrer à 50 Hz !
Parfois, avec les très gros transformateurs, la carcasse métallique même du transformateur vibre sous l’effet du champ magnétique. On appelle ça la magnétostriction et c’est ce qui produit le bruit caractéristique des transformateurs ou même des moteurs électriques (train, voiture électrique, métro…).
Les détecteurs antivol dans les supermarchés fonctionnent également avec des champs magnétiques alternatifs. Ces derniers sont émis par les portiques antivol aux casses ou à la sortie du magasin. Si on essaye de faire passer un article muni d’un dispositif antivol, ce dernier réagit et émet son propre champ magnétique. Ce dernier est ensuite capté par le portique et il sonne.
Vous pouvez passer par un tel portique en tenant un aimant dans la main (rassurez-vous, un aimant permanent ne fait pas sonner les portiques) : il vibrera et vous le sentirez.
Détecter les faux billets
Parmi les nombreuses mesures de protections contre la contrefaçon utilisée sur les billets de banque, il y a l’encre ferromagnétique.
Il s’agit d’une encre dont un des ingrédients contient de l’oxyde de fer, qui réagit à un aimant : le billet est attiré par l’aimant. Les billets en euro (la première série) contient également cette mesure de sécurité et si vous avez un aimant puissant, vous pouvez réussir à attirer certaines parties du billet vers l’aimant :
Notez bien que tout le billet n’est pas magnétique, seules certaines portions le sont. Mais en baladant l’aimant dessus, vous trouverez assez vite les portions concernées.
Certains détecteurs de faux billets fonctionnent en testant la présence et la position de la bande magnétique sur le billet. D’autres détecteurs pratiquent le test à la lumière UV (certaines encres sont fluorescentes), d’autres aux infrarouges, ou encore à la présence de symboles ou inscriptions particulières (constellation EURion).
D’où vient la résistance du verre Pyrex® ?
Couleur science par Anonyme le 16/02/2023 à 06:34:00 - Favoriser (lu/non lu)

Le Pyrex® est un type de verre qui ne se brise pas, ou beaucoup plus difficilement, sous l’effet d’un choc thermique. Il est utilisé en cuisine pour les plats qui vont au four par exemple, ou dans l’équipement de laboratoire, parfois sujets à des gradients de températures élevés : tubes à essais, béchers, etc.
Pourquoi ce verre résiste-t-il à la température et pas le verre ordinaire ?
Une question de dilatation
La température constitue le degré d’agitation des molécules au sein de la matière. Le plus souvent, si la température monte, l’agitation augmente et les atomes ont besoin de plus d’espace ce qui dilate la matière. C’est ce qu’on appelle la dilatation thermique.
Certains matériaux se dilatent plus que d’autres. Une barre de métal courant de 1 m de long gagne environ 15 à 25 µm par degré. On dit que son coefficient de dilatation est de 15-25 µm⋅m⁻¹⋅K⁻¹, ou tout simplement 15 à 25 × 10⁻⁶ K⁻¹. Pour le verre ordinaire, il est autour de 9 × 10⁻⁶ K⁻¹, soit moitié moins.
La différence de coefficient de dilatation thermique ne fait pas tout. Si on chauffe un verre lentement mais à très haute température, et qu’on le laisse refroidir très lentement ensuite, il n’y aura aucun problème : il ne se brisera pas. Les problèmes naissent si le refroidissement est brutal, et surtout, local. Dans ces cas-là, certaines zones du verre se refroidissent et se contractent pendant que d’autres sont encore chaudes et dilatées. C’est cela qui va casser le verre. Et là, c’est dû à la rigidité du verre.
Les métaux ne sont pas affectés, car ils sont malléables : les liaisons entre les atomes sont flexibles et peuvent se défaire et se reformer. Si une région du métal a des liaisons plus longues suite à un échauffement, ce n’est pas grave : ces liaisons se déplacent et s’étirent.
Dans le verre, qui n’est absolument pas malléable et très dur, les liaisons ne peuvent pas s’étirer : elles se brisent. C’est pour ça que le verre casse sous l’effet de la température, mais aussi d’un choc ou d’une déformation :
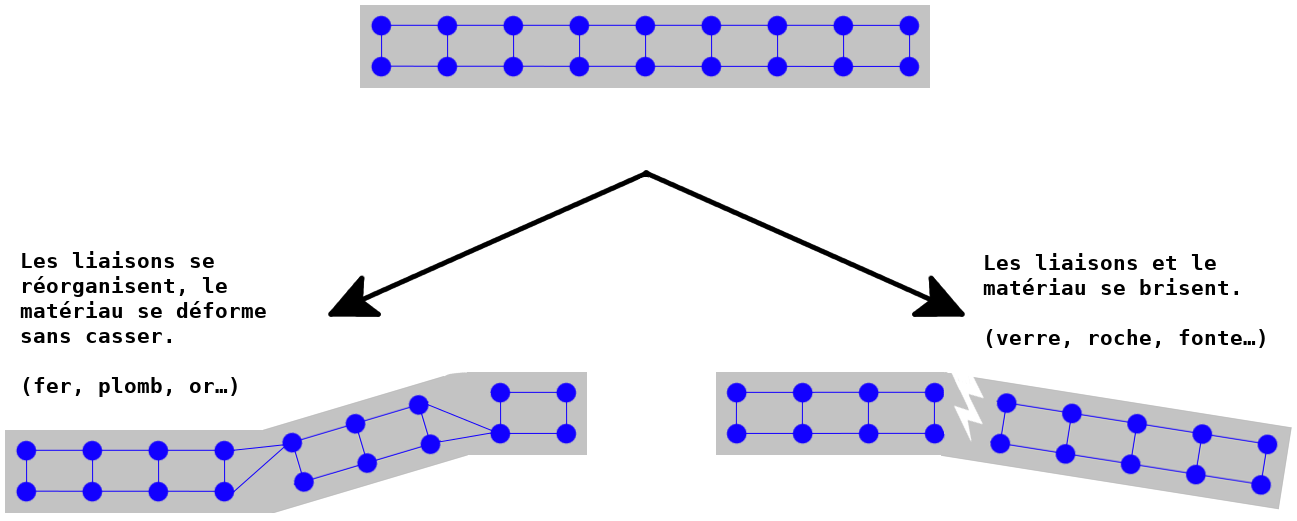
Le verre ordinaire a donc deux propriétés qui vont très mal ensemble :
- les différences de températures le déforment ;
- ses liaisons atomiques sont indéformables et se cassent sous la contrainte.
On comprend donc que si le verre est chauffé ou refroidi trop brusquement, il casse. Pour éviter ça, on peut agir sur l’un des deux paramètres : soit créer un produit déformable (plastique, métal…) soit créer un matériau qui ne se dilate pas sous l’effet de la température.
De l’introduction du borax
Les verres, similairement aux alliages métalliques, sont des mélanges bien dosés de plusieurs substances : on utilise généralement un matériau de base mais dans lequel on rajoute des ingrédients pour en modifier les propriétés. Le cristal en est un exemple : utilisé pour faire des coupes ou des verres, c’est un verre dans lequel on incorpore du plomb, ce qui en modifie les propriétés optiques et acoustiques notamment.
Pour le Pyrex, c’est du bore que l’on a ajouté, sous forme de borate de sodium, ou borax (un minéral) dans une base ordinaire en silicate. Ceci modifie la structure moléculaire du verre et en réduit le coefficient de dilatation thermique : de 9 × 10⁻⁶ K⁻¹, on passe à 3 × 10⁻⁶ K⁻¹.
Pour une même différence de températures, les contraintes mécaniques induites par la dilatation localisée du verre sont divisées par 3. Ceci suffit amplement aux températures subies par un plat de cuisine : le verre borosilicaté peut supporter des différences de température de ~180 °C, contre ~55 °C pour le verre ordinaire.
Température VS différence de température
Il faut bien insister sur le fait que c’est la différence de température qui fait que le verre se brise. Si vous chauffez un verre uniformément, il ne se passera absolument rien. En faisant ça, toutes les liaisons atomiques se dilatent ensemble et cela ne pose pas de problème. Même chose lors d’un refroidissement. C’est pour ça qu’un verre de cuisine peut aussi bien contenir du thé chaud, qu’un soda avec des glaçons.
Ce qu’il faut éviter, c’est de refroidir certaines zones et en chauffer d’autres, comme plonger un verre rempli de glace dans une bassine d’eau bouillante : l’extérieur chauffé se dilate et tire sur la partie restée froide et cela casse.
Même chose pour un pare-brise : il résiste aussi bien au Soleil en été qu’à la glace en hiver. Mais si vous jetez de la glace dessus en plein été, ou de l’eau chaude en hiver, la différence soudaine de température fera casser le verre à cause des contractions ou dilatations localisées du verre. Si vous voulez dégivrer un pare-brise avec de l’eau, n’utilisez donc pas de l’eau chaude, mais de l’eau froide (10-15 °C) : cela suffit pour fondre la glace, sans toutefois casser la vitre.
D’autres matériaux intéressants
Il est incroyable que l’on arrive aujourd’hui à proposer des matériaux avec des propriétés aussi intéressantes. Autrefois, les vitraux étaient faits en verre coloré scellés dans du plomb. En effet, le plomb est malléable et facile à façonner. Le fer ou l’acier sont beaucoup plus communs et durs, mais le fait qu’ils soient aussi plus rigides pose problème en cas de fort gradient de température : leur dilatation risque de déformer le vitrail et de casser le verre, alors que le plomb, malléable, prend la déformation pour lui.
Pour de hautes températures on utilise aujourd’hui un alliage à base de nickel et le fer appelé le covar : son coefficient de dilatation est proche de celui du verre. En cas de chauffe, une structure verre-covar se dilate donc uniformément sans qu’un des constituants ne tire sur l’autre. C’est une variante d’un autre alliage : l’invar, dont le coefficient de dilatation est très faible (
Dans les conditions de température extrêmes, comme les ampoules lumineuses très haute puissance (projecteur de cinéma par exemple), est généralement utilisé de la verrerie en quartz. Ce dernier, bien que plus cher à produire, a un coefficient de dilatation thermique extrêmement faible et résiste particulièrement bien aux forts changements de température.
Comment fonctionnent les spray anti-buée pour lunettes ?
Couleur science par Anonyme le 02/02/2023 à 05:25:00 - Favoriser (lu/non lu)

Les lunettes, tout comme les miroirs de salle de bain ou encore les vitres de voitures, ont tendance à former de la buée quand l’air est humide et qu’il fait froid. Il existe des sprays « antibuée » censés prévenir la buée et maintenir une bonne visibilité.
Comment fonctionnent ces sprays ? C’est l’objet de l’article. Un indice : c’est une question de tension de surface de l’eau !
Pourquoi se forme de la buée ?
Pour savoir ce qui se passe, il faut déjà savoir pourquoi il se forme de la buée et pourquoi elle détériore la visibilité.
La buée n’est autre que de l’humidité qui condense sur une surface froide, dans le cas présent, un verre de lunette ou une vitre. L’eau contenue sous forme de gaz dans l’air redevient liquide au contact de la vitre froide et y adhère.
À cause de la tension de surface de l’eau, les molécules d’eau sont davantage attirées entre-elles qu’au verre. Il en résulte que l’eau a tendance à prendre la forme de gouttelettes bien rondes au lieu de former un film uniforme sur tout le verre.
Dans ces conditions, le verre mouillé, bien que toujours transparent, altère totalement l’image par diffraction :

C’est ce phénomène que l’on cherche à prévenir ici, et une solution est alors d’agir sur la tension de surface de l’eau.
La tension de surface
La tension de surface — ou tension superficielle — je l’ai dit, provient du fait que les molécules sont très fortement attirées les unes aux autres. Une molécule au cœur d’un récipient d’eau attire l’eau partout autour d’elle, mais en surface, la molécule ne peut attirer que celles situées en surface. Vu qu’il y a moins de molécules d’eau, la force de cohésion n’en est que plus forte en surface : l’eau forme donc comme un film, et ce dernier est suffisamment résistant pour y faire flotter un trombone, par exemple :

Dans le cas de la condensation, ce processus entraîne la formation de gouttelettes arrondies, ce qui permet à l’eau de minimiser la surface totale tout en maximisant la quantité d’eau dans une goutte. La forme géométrique dont le ratio volume / surface est le plus grand est en effet une sphère. La taille maximale des gouttes est ensuite limitée par la gravité et la force de cohésion avec le verre.
Il est totalement possible de briser cette tension de surface : cela se fait en empêchant les molécules d’eau d’être liées entre-elles !
Le rôle d’un tensioactif
Un produit qui s’insère dans un liquide, vient se positionner entre les molécules et réduit la tension de surface, s’appelle un tensioactif.
L’alcool ou le savon sont des tensioactifs. Vous pouvez essayer : si vous avez votre trombone qui flotte sur l’eau, versez une goutte de savon ou de produit vaisselle dans le verre et le trombone coulera aussitôt. Le tensioactif aura alors séparé les molécules d’eau et la tension de surface diminue : le trombone n’est alors plus soutenu et il coule.
Dans le cas des sprays pour lunettes, le tensioactif est généralement un alcool (de l’alcool isopropylique) ainsi qu’un produit détergeant similaire au savon qui forme un film persistant sur le verre. Quand l’eau vient s’y condenser, ce dernier ne cherche pas à former des gouttes d’eau arrondies, mais plutôt un film d’uniforme épaisseur. Résultat : il n’y a plus de déformation de l’image :

En prime, vu que la surface de contact est beaucoup plus grande avec le verre, l’eau y capte davantage de chaleur et s’évapore plus rapidement !
Une autre solution : réchauffer le verre
La méthode que tout le monde connaît, et qu’on utilise dans une voiture ou une salle de bain, est de souffler de l’air chaud sur la vitre. Cela permet de faire évaporer l’eau qui s’y condense. Jusque là, rien de nouveau. Mais s’il était possible de récupérer la chaleur ambiante, ou le rayonnement invisible du Soleil pour réchauffer le verre sans pour autant bloquer la lumière ?
Ceci est justement ce qu’a fait un groupe de scientifiques suisses. Ces derniers ont publié un papier où ils expliquent avoir développé un traitement de surface constituée d’une fine couche d’or emprisonnée entre deux réseaux de dioxyde de titane. L’ensemble mesure moins de 10 nm d’épais. L’effet de cette nanostructure est d’absorber le rayonnement infrarouge et de le convertir en chaleur, tout en laissant passer la lumière visible.
La moitié du rayonnement solaire naturel, même indirect, par exemple lorsqu’il fait nuageux, est composé d’infrarouge invisible. Toute cette énergie est captée par la couche d’or qui la transforme en chaleur. Ceci réchauffe alors le verre et fait partir la buée.
Le réchauffement du verre, selon les chercheurs, serait jusqu’à +8 °C par rapport à la température ambiante, tout ça en restant transparent à la lumière visible, et donc parfaitement adaptée aux lunettes ou aux vitres.
Les verres ainsi traités se désembuent quatre fois plus rapidement qu’un verre ordinaire et sont également plus efficaces pour prévenir la formation de buée initialement.
Conclusion
Les sprays ou lingettes antibuée fonctionnent, car elles contiennent des tensioactifs : des molécules qui réduisent la tension de surface du liquide. L’eau ne cherche plus à former des gouttes qui déforment l’image, mais forme un film uniforme dont l’effet sur la vision est pratiquement nul.
Voici ce que cela donne sur une surface vitrée :

Quant à d’autres méthodes, notamment à base de nanotechnologies, sont activement en développement : le papier sur la fine couche d’or a été publiée juste quelques jours après que j’eus fini d’écrire cet article !
Maintenant que toutes le unités SI sont définies par des constantes naturelles, vont-elles encore changer ?
Couleur science par Anonyme le 19/01/2023 à 05:03:00 - Favoriser (lu/non lu)

En 2018, la 26ᵉ Conférence générale des poids et mesure (CGPM) a décidé de poser une nouvelle définition du kilogramme. Cette unité était alors la dernière des unités de base à encore être définie à partir d’un artefact matériel — la masse d’un bloc de platine stocké à Paris — et non une constante universelle de la nature. D’autres unités furent également redéfinis, comme le kelvin ou l’ampère.
Depuis 2018, donc on a un système d’unités cohérent, sans artefact matériel périssable ou fragile. Ainsi, le BIPM, ayant rempli sa mission de proposer un système d’unités complet et inaltérable, a été dissout et tout va pour le mieux dans le meilleur des mondes.
Non ? Non.
Bien-sûr, tout ne s’est pas arrêté, et en 2022, soit quatre ans après, s’est tenu la 27ᵉ réunion de la CGPM. Divers nouvelles propositions ont été faites et validées, avec notamment l’ajout de quatre nouveaux préfixes : quetta, ronna, ronto, quecta.
Une autre mesure importantes est d’avoir lancé le projet d’une éventuelle redéfinition de la seconde. Pourquoi ?
Pourquoi refaire ce qui a déjà été fait depuis 1960, à savoir disposer d’une définition précise de la seconde ?
Histoire de la seconde
L’histoire des unités de mesure est passionnante. Aussi, la recherche d’un système d’unités commun à tout le monde ne date pas d’hier. Déjà avant le Moyen Âge, on cherchait à unifier les moyens d’échanges commerciaux entre les régions et les royaumes, qui avaient tous leurs propres étalons de longueur (pied, pouce, yard, aune, coudée, verge…) ou de poids (livre, livre sterling, once, quintal, stone…). Aussi, sans un système de vérification derrière, les marchants peu scrupuleux n’hésitaient pas à trafiquer les masses marquées ou les balances à leur avantage, provoquant là également des dérives et des conflits.
Le système métrique, né de la révolution française et adopté partout dans le monde aujourd’hui (ou presque) permit de mettre fin à ces pratiques, en tout cas de poser un cadre fixe et légal à la métrologie internationale.
De façon intéressante, l’unité de la mesure du temps, la seconde, n’avait pas ce problème. Il faut croire que la division en vingt-quatre d’une journée date d’une époque tellement lointaine, à savoir l’Égypte Antique, que le monde entier en a hérité. La division en 24 heures de la journée, puis de chaque heure en 60 minute et chaque minute en 60 secondes se retrouve partout et a demeuré jusqu’à nous. Et même si les révolutionnaires français ont tenté de modifier ça dans le but de passer à des journées de 10 heures et des heures de 100 minutes, cette idée-là n’a jamais prise et fut rapidement abandonné.
Maintenant, avoir une seconde définie à partir d’une fraction de 1/24 × 1/60 × 1/60 de la rotation de la Terre est bien joli, mais c’est sans compter que nos instruments de mesures sont devenus de plus en plus sensibles. À un point que l’on a fini par constater que la rotation terrestre elle-même n’avait pas grand-chose de régulier ! Autrement dit, l’on avait une définition de la seconde qui variait d’année en année.
Ceci était inacceptable. La solution mis en place alors : définir la seconde comme une fraction d’une année bien précise, l’année 1900 et aucune autre. Ceci fut la définition de la seconde entre 1956 et 1967. Puis, elle fut changée à nouveau parce qu’on avait beaucoup mieux. Depuis 1967, la définition de la seconde fait intervenir des périodes d’oscillation de radiations émises par des atomes et mesurées avec l’aide d’horloges atomiques.
Une seconde est désormais le temps mis pour qu’une radiation émise par une transition hyperfine de l’atome de césium 133 à l’état fondamental oscille 9 192 631 770 fois.
Les horloges atomiques permettent de mesurer les durées de façon exacte jusqu’à la 14ᵉ décimale, ce qui fait de cette unité celle qui est la mieux définie parmi toutes les unités du système international.
Pourquoi changer la seconde ?
Avec la définition précédente, on pourrait penser qu’on a enfin une définition stable et définitive de la seconde. Sauf que ce n’est pas si simple.
La mise en œuvre de cette définition fait intervenir un appareil, à savoir une horloge atomique dont le fonctionnement (décrit dans mon article sur l’horloge atomique) peut être résumé ici.
Tout d’abord, il faut savoir que les atomes et leurs électrons ont une fréquence de vibration propre. Un certain nombre d’oscillations de ces vibrations correspond à un temps d’une seconde. Problème : comment mesurer ces vibrations ? Comment les compter ?
Tout d’abord, on a décidé qu’une seconde correspondait à 9 192 631 770 oscillations de la lumière émise par le césium 133. Cette durée a été estimée à partir de la définition précédente, puis on a décidé que ça serait la nouvelle définition. Maintenant, comment mesurer 9 192 631 770 oscillations ?
La solution est d’utiliser une horloge atomique. Il s’agit d’envoyer un rayonnement micro-onde sur des atomes de césium 133. Si ce rayonnement a une fréquence approximative de la fréquence de vibration du césium, alors les atomes entrent en résonance et il passe dans un état excité.
L’idée est donc, une fois qu’on envoie le rayonnement micro-onde sur les atomes, de compter le nombre d’atomes dans leur état excité. En faisant varier la fréquence du rayonnement micro-onde, on fait varier la proportion d’atomes excités. Il suffit donc de trouver le rayonnement micro-onde qui excite le mieux les atomes. Une fois qu’on a trouvé la bonne fréquence, il suffit de dire que cela correspond à 9 192 631 770 hertz, car c’est ce qu’on a défini comme étant « une seconde ».
Ensuite, on divise la fréquence de ce rayonnement par 9 192 631 770, et on obtient un compteur de 1 Hz, soit une oscillation par seconde, et nous voilà avec notre horloge.
Maintenant pourquoi ceci n’est pas infiniment précis ? Tout simplement parce que notre machine à micro-ondes n’est elle-même pas infiniment précise ! La machine affiche bien 9 192 631 770 Hz, mais qui sait si l’on est plutôt à 9 192 631 770,3 Hz ou plutôt à 9 192 631 769,8 Hz ?
Oui, la différence est minime — on parle d’une résolution en picosecondes — mais en métrologie, cette différence compte. Aussi, avec la technologie récente, on sait mettre en pratique des fréquences dont la résolution est plus fine que ça d’un facteur 100 environ. Autrement dit, on pensait avoir le chronomètre le plus précis du monde, mais aujourd’hui on en fait un 100 fois plus précis ! Dans ces conditions-là, c’est bien ce nouveau chronomètre qu’il faut utiliser pour mesurer le temps universel utilisé par tout le monde, non ?
Cette conclusion est également celle à laquelle la BIPM est parvenue, et lors de la 27ᵉ réunion de la GCPM, a ouvert la voie pour « la future redéfinition de la seconde ».
Quelle importance dans le système métrique ?
On peut penser que redéfinir une unité, de temps en temps, parce qu’on a inventé un dispositif plus fiable et plus exact que le précédent est quelque chose de normal. Et ça l’est. Le truc c’est que dans le cas de la seconde en particulier, cette redéfinition est d’autant plus importante.
Déjà, je l’ai dit : la seconde est déjà l’unité la plus précisément définie. Descendre encore plus bas relève donc en soi d’un exploit. Mais ce n’est pas tout : modifier la seconde a des conséquences sur toutes les autres unités !
En effet, bien que l’on parle ici d’unités de base, rien n’empêche leur définition de les lier entre-elles. Ainsi, la définition du mètre fait intervenir la seconde : le mètre est le trajet de la lumière durant une fraction 1/299 792 458 seconde. L’ampère, quant à lui, correspond à une quantité de charge qui traverse un fil électrique… durant une seconde également !
De la même manière, depuis la redéfinition en 2018 du kilogramme, de l’ampère et du kelvin, toutes les unités (mise à part la mole) dépendent de la seconde.

Autrement dit, redéfinir la seconde aura une implication sur les autres unités.
Toutes les unités sont aujourd’hui définies à partir de définitions de constantes physiques : le mètre dépend de la vitesse de la lumière, le kilogramme dépend de la constante de Planck, etc. Si ces constantes sont numériquement exactes, il faut tout de même utiliser un appareil de mesure pour retrouver nos unités. C’est là qu’intervient une incertitude de mesure.
Ainsi, définir la seconde avec une horloge atomique au césium nous la donne avec une précision de 10⁻¹⁶ près. Le kilogramme, lui est défini à partir de la constante de Planck et sa mesure se fait avec une précision de 10⁻⁸ environ. Vu que le kilogramme dépend de la seconde, les incertitudes se combinent. Si maintenant l’incertitude dans la mesure de la seconde diminue, grâce à une meilleure sensibilité de la mesure, alors l’incertitude dans la mesure du kilogramme s’en trouve également améliorée.
Vu que toutes les unités dépendent de la seconde, ce sont donc toutes les mesures des unités qui pourraient en bénéficier ; ou en tout cas cela ne pourra pas nuire à leur mesure, vu que la seconde est déjà définie avec une précision beaucoup plus importante.
À qui cela va profiter ? Quel intérêt ?
Avoir des unités toujours plus précises ne peut pas nuire, déjà.
Ensuite, le fait d’avoir des horloges capables de nous donner l’heure avec une résolution allant jusqu’à la nanoseconde est utile dans la vie courante : tous les ordinateurs actuels fonctionnent à cette échelle. Sans ceci, ces derniers ne fonctionneraient pas. Les télécoms, ou encore le système GPS, eux, ont besoin de précision supplémentaire, donnée par des horloges atomiques.
Maintenant, arriver à mesurer des intervalles de temps encore plus fins permettra de déceler des variations de distance plus fine également (le mètre dépend de la seconde, je le rappelle). Ceci pourrait servir par exemple dans la mesure des ondes gravitationnelles en provenance de l’espace. Rien pour la vie courante, mais la recherche fondamentale — qui elle, au sens large, a des implications dans la vie courante — s’en trouvera améliorée.
Un autre exemple peut-être des mesures plus précises dans les champs de pesanteur terrestre : la sensibilité des horloges atomiques optique est telle qu’on détecte les effets relativistes quand on soulève l’horloge d’un centimètre, par exemple.
Avec une telle sensibilité, on peut espérer détecter des variations dans la structure interne de la Terre : mouvement des plaques continentales, typiquement. Il n’y a qu’un pas pour dire que ça servira pour, éventuellement, prédire les séismes ou les éruptions volcaniques.
Pourquoi la fumée bleue de cigarette devient blanche quand on l’expire ?
Couleur science par Anonyme le 05/01/2023 à 19:30:00 - Favoriser (lu/non lu)

Avez-vous parfois constaté que toutes les fumées n’ont pas la même couleur ? Certaines sont blanches, d’autres noires… Et même hors du cadre d’un conclave, on peut trouver quelque chose à dire sur tout ça.
En l’occurrence, les fumées noires sont essentiellement constituées de suie imbrûlée et de particules lourdes, c’est-à-dire bien plus grosses que de simples molécules. Les fumées blanches sont plutôt chargées de vapeur d’eau et forment des nuages (entre autres molécules invisibles et plus ou moins polluantes évidemment).
Mais qu’en est-il des fumées bleues, comme celles observées avec une cigarette ? Et pourquoi, cette même fumée, devient-elle blanche lorsqu’elle est expirée ?
Ce phénomène curieux fait l’objet de cet article. Et non, ce n’est pas une raison pour se mettre à fumer.
La fumée bleue : une question de taille
Ce qui détermine la couleur d’une substance gazeuse, comme une fumée, c’est la façon dont les molécules du gaz interagissent avec la lumière. En particulier, comment et par quel mécanisme la lumière est diffusée — déviée — par le gaz.
Une des formes de diffusion possible est la diffusion de Rayleigh.
Cette diffusion existe quand les particules sont bien plus petites que la longueur d’onde de la lumière. Pour le visible, cela signifie une taille de l’ordre de 100 nm (0,1 µm) maximum.
Cette diffusion se produit alors si les particules se trouvent sur la trajectoire d’un rayon lumineux : l’onde lumineuse, qui n’est autre qu’une oscillation du champ électromagnétique, provoque une oscillation des électrons des atomes qu’elle rencontre et ces derniers vont renvoyer leur propre lumière, identique à celle qui a provoqué la vibration. Il en résulte que la lumière est renvoyée dans toutes les directions autour de cet atome :

L’intensité de la diffusion de Rayleigh dépend de la longueur d’onde de la lumière diffusée. Plus précisément, cette dépendance est à la puissance −4. Cela signifie que si la longueur d’onde est multipliée par 2, alors la diffusion est divisée par 16 (car 2⁻⁴ = 1/16). Une faible augmentation dans la longueur d’onde constitue donc une réduction importante dans la diffusion de cette longueur d’onde. Ce que cela signifie pour nous est que le bleu est fortement diffusé, et les autres couleurs, nettement moins.
Tout ce processus est ce qui se produit avec la fumée de cigarette : cette fumée est très fine (les particules sont plus fines que 100 nm) et sous la lumière blanche, le bleu est renvoyé dans toutes les directions, y compris vers l’observateur, alors que les autres couleurs continuent leur chemin en ligne droite, car elles sont peu ou pas diffusées. La fumée nous apparaît donc bleutée.
Et pour la fumée expirée, qui est blanche ?
Maintenant, quand un fumeur inhale la fumée et l’expire quelques instants après, les particules ne sont plus sous le même état dans l’air expiré. L’air dans les poumons est très humide, et cette humidité se condense sur les impuretés. Ici, les particules de la fumée vont produire de petites gouttelettes.
Ces gouttelettes sont beaucoup plus grosses et la diffusion de Rayleigh ne fonctionne plus. La diffusion qui a lieue à présent est appelée diffusion de Mie, qui correspond à la diffusion obtenue quand les particules sont bien plus grosses que la longueur d’onde incidente.
Quand on éclaire cette fumée constituée de gouttelettes d’eau, toutes les longueurs d’ondes sont diffusées dans les mêmes proportions et la lumière blanche est déviée dans sa globalité : la couleur de la fumée est… blanche.
C’est pour ça que je disais plus haut que l’on observe en réalité un nuage : eux aussi sont composés de gouttelettes d’eau, comparativement grosses par rapport aux molécules. Et c’est aussi la raison pour laquelle les nuages sont blancs : toute la lumière y est diffusée par le principe de la diffusion de Mie.
Et pour la complétude : l’origine de la couleur bleue de la fumée est également celle de la couleur bleue du ciel : les très fines impuretés, les molécules elles-mêmes et les variations dans la densité de l’air produisent la diffusion de Rayleigh. Le bleu nous vient donc de tous les côtés, alors que les autres couleurs, le jaune, rouge, vert, orange… nous provient seulement directement du Soleil, qui est donc jaune-blanc.
Pourquoi le champagne et les boissons gazeuses pétillent-elles ?
Couleur science par Anonyme le 15/12/2022 à 06:11:00 - Favoriser (lu/non lu)

Vous connaissez très probablement les boissons gazeuses, telles que le Coca, de la limonade, de l’eau gazéifiée, ou encore le champagne. Mais pourquoi ces boissons piquent ?
Est-ce que ce sont bulles qui piquent ? Non, pas directement !
Une question d’acide
Toutes ces boissons sont à base d’eau dans laquelle on dissout du dioxyde de carbone, le CO2. Ce dernier est un gaz, mais cela reste un composé qu’il est possible de dissoudre dans l’eau. Le dioxygène, O2, un autre gaz, est aussi soluble dans l’eau : c’est comme ça que les poissons arrivent à respirer sous l’eau, grâce à leurs branchies.
Une fois dissoute, le CO2 réagit avec l’eau pour former de l’acide carbonique :
Cette réaction se fait toute seule dès lors qu’on met de l’eau en contact avec du CO2, mais se produit mieux sous pression. Les boissons gazeuses sont d’ailleurs préparées sous pression, pour maximiser la teneur en CO2 et donc en bulles.
Cette réaction est également réversible : si l’on diminue la pression, l’acide carbonique se décompose en eau et CO2 et ce dernier forme des bulles qui remontent alors à la surface. C’est ce qui se produit lorsqu’on ouvre une bouteille de boisson pétillante pour la première fois.
Cependant ce ne sont pas les bulles qui produisent la sensation de picotement. D’une, si c’était le cas, alors le picotement serait ressenti par exemple avec un doigt que l’on plongerait dans la limonade. Or ce n’est pas le cas. Si cela picote en bouche, et essentiellement sur la langue, c’est une affaire liée au sens du goût.
L’acide carbonique reste avant tout un acide : c’est ce qui donne à l’eau gazéifiée ce petit goût acidulé. Si l’eau est fortement gazéifiée, comme c’est le cas dans les boissons gazeuses, l’acide carbonique a pour effet d’activer sur la langue les mêmes récepteurs que ceux activés par la moutarde ! C’est ça qui provoque ce picotement.
Maintenant, l’effet est très court : l’acide finit par se décomposer et l’effet ne dure pas, à la différente de l’effet du piment par exemple, qui reste quand-même longtemps en bouche.
Et les boissons « light » ?
On remarque assez bien, que ce soit au goût au bien avec la fameuse expérience « coca-menthos », que les boissons allégées en sucres, ou « light », contiennent plus de bulles. Ceci est lié essentiellement à la solubilité du gaz dans l’eau de la boisson et de la facilité des bulles à se former lorsqu’on ouvre la bouteille.
Quand la pression est relâchée lors de l’ouverture, l’acide carbonique peut se décomposer en eau et en CO2, mais ce dernier doit pouvoir repousser de l’eau afin de former des bulles. Or, il intervient ici la notion de tension de surface de l’eau, qui empêche la formation de ces bulles s’il n’y a pas assez de CO2 pour constituer une bulle.
Dans les boissons light, le sucre est retiré, mais des édulcorants comme l’aspartame sont ajoutés à la place. Or ce produit a le pouvoir de réduire la tension de surface de l’eau : on dit que c’est un tensioactif. Sous son effet, l’eau résiste moins à la formation de bulles et elles sont plus nombreuses, et plus petites aussi.
Et avec d’autres gaz ?
Certaines bières contiennent de l’hélium, non pas pour le goût, mais pour s’amuser à avoir cette voix de Donald Duck quand on parle (une question d’absorption de certaines fréquences dans le gaz).
Ces bières contiennent toujours du CO2 (produits par la fermentation), et restent donc piquantes à cause de ça, sans que l’hélium n’y change quoi que ce soit.
En principe, donc, une boisson dont les bulles sont exclusivement formées par autre chose que du CO2 ne piqueraient pas, ou en tout cas pas de la même façon. Ceci reste difficile à tester toutefois, car le CO2 est environ 50 fois plus soluble que l’oxygène ou le diazote, tous les deux constituants de l’air. Les quelques gaz plus solubles dans l’eau que le dioxyde de carbone comprend par exemple le dichlore ou le sulfure d’hydrogène, qui sont très ou extrêmement toxiques, et peu recommandables.
Certaines autres substances, comme la chantilly contiennent des gaz dissous également, en l’occurrence du protoxyde d’azote. On utilise spécifiquement ce gaz, car il est liposoluble (soluble dans le corps gras de la crème) alors que le CO2, acide, on l’a vu, risque de faire tourner la crème.
Ceci étant dit, le protoxyde d’azote ne produit pas de pétillement. Il reste néanmoins du gaz hilarant (le gaz hilarant est du protoxyde d’azote), il ne faut pas en abuser non plus.
Conclusion
Pour conclure : ce ne sont pas les bulles elles-mêmes, ni leur éclatement qui piquent quand on boit une boisson gazeuse. Il semble que l’effet soit dû spécifiquement à l’action de l’acide carbonique, un acide formé par réaction d’hydratation du CO2 par l’eau.
Le CO2 est utilisé car il est facilement soluble dans l’eau, contrairement à d’autres gaz courants, et sans danger.
Le CO2 est aussi le gaz qui est produit lors de la fermentation alcoolique de certains jus de fruits, un processus où des micro-organismes transforment les sucres en alcool. Dans le vin, on laisse ce gaz s’échapper jusqu’à la fin de la fermentation. Pour le champagne, le cidre ou encore la bière, la fermentation se fait dans un contenant fermé qui force le gaz à rester. Dans ce cas, la pression monte, le CO2 se dissout dans l’eau et on obtient des boissons à bulles.
Références
- The secret behind soda's bite? Not bubbles, study finds. - Los Angeles Times
- FYI: Why Do Humans Like Fizzy Drinks? | Popular Science
- Why Is Diet Coke So Fizzy? | Office for Science and Society - McGill University
- The Sparkle of Carbonated Water | Office for Science and Society - McGill University
- Solubilities of Gases in Water at 293 K
Pourquoi le maïs forme du pop-corn ?
Couleur science par Anonyme le 01/12/2022 à 18:43:00 - Favoriser (lu/non lu)

Le pop-corn est ce que l’on obtient quand on chauffe très fortement les grains de certaines variétés de maïs : le grain de maïs, petit et rond, éclate subitement et prend beaucoup de volume. Comment ça se passe ?
Une histoire de polymères
Le grain de maïs est essentiellement constitué d’amidon : un polymère naturel du sucre, autrement dit un long enchaînement de molécules de glucose. Il contient également un peu d’eau. L’amidon et l’eau sont piégés dans le grain lui-même par la peau, appelé le péricarpe, du grain.
Lorsque l’on chauffe tout ça autour de 180 °C, on assiste à plusieurs phénomènes.
Pour commencer, l’amidon solide et dure devient gélatineuse, pratiquement liquide. L’eau quant à elle monte également en température. En temps normal, à 180 °C, elle se serait vaporisée, mais là elle reste liquide à cause de son confinement dans le grain. Incapable de se vaporiser, elle va monter en pression : on parle d’environ 9 fois la pression atmosphérique, soit environ quatre fois la pression d’un pneu de voiture !
Soumis à un tel effort, le péricarpe finit par céder. À ce moment, l’eau et l’amidon gélatineux ne sont plus retenus : l’eau peut se détendre et revenir à la pression atmosphérique et se vaporiser, et elle fait cela directement dans l’amidon.
Il en résulte que l’amidon prend jusqu’à 30 fois son volume et devient une sorte de mousse : une structure aérée constituée d’alvéoles pleines de gaz (de vapeur, en l’occurrence).
Qui plus est, tout comme la compression d’un fluide tend à l’échauffer, la détente tend à la refroidir. Lorsque le grain de maïs cède, l’eau va rapidement se détendre, se vaporiser et se refroidir, passant immédiatement de 180 °C à 135 °C. Ceci a pour conséquence de recristalliser l’amidon : la mousse obtenue est alors figée et durcie : le pop-corn est prêt.
Enfin, comme l’éclatement d’un grain de maïs sous 9 bars de pression est assez violent, l’amidon commence à être éjecté du grain dès la formation des premières fissures : c’est cela qui forme les « ailes de papillon » d’un grain de pop-corn :
Un processus similaire du polystyrène expansé
L’amidon, ce polymère du glucose, qui s’expanse sous l’effet de la vapeur d’eau, n’est pas sans rappeler un autre produit que vous avez sûrement déjà vu : le polystyrène expansé.
Je dis bien « expansé » car le polystyrène de base ne l’est pas forcément : le plastique qui forme les pots de yaourt, par exemple, est du polystyrène non-expansé : il n’est pas sous forme de mousse.
Pour obtenir du polystyrène expansé, on utilise une émulsion de styrène (le monomère, le maillon de la chaîne du polystyrène) dans de l’eau. Quand on commence à polymériser le styrène pour former du polystyrène, on ajoute un fluide, du pentane typiquement : ce dernier va imprégner le polystyrène en train de se former.
Ici, on recrée en réalité les conditions d’un grain de maïs, à savoir un fluide (l’eau ou le pentane) imprégnant un polymère (l’amidon ou le polystyrène). Ensuite, il suffit de chauffer fortement avec de la vapeur et le polymère devient mousseux puis se fige.
Dans le cas du polystyrène expansé, ce dernier est généralement directement moulé pour lui donner la bonne forme.
Le polystyrène, comme le pop-corn est très léger et peu dense. Mais dans les deux cas, il suffit de les plonger dans un solvant pour le condenser rapidement : la structure de mousse s’effondre et tout l’air présent dans la mousse est relâchée. C’est ce qui se passe quand on plonge un pop-corn dans de l’eau.
Conclusion
Comme tout processus, le pop-corn se forme par une succession d’événements provoqués par un ensemble de conditions réunies. En l’occurrence, le grain de maïs plein d’amidon doit également contenir un peu d’eau (14 % idéalement), être bien étanche (la variété « butterfly » convient pour ça) et l’ensemble doit être chauffé à environ 180 °C.
Ensuite, le grain éclate et l’eau qui s’évapore au milieu de l’amidon provoque l’expansion de ce dernier qui se fige enfin formant une mousse volumineuse mais très légère.
Ce processus est identique à celui qui permet la création du polystyrène expansé. Par ailleurs, les composés d’amidon expansé (pop-corn) sont utilisés pour remplacer le polystyrène dans certains cas, comme celui d’absorbeur de chocs dans les colis par exemple, comme absorbeur de chocs.
Liens et références
Liens :
- Le pop-corn, c’est emballant | Pour la Science
- Pourquoi le POPCORN explose ? − YouTube (par Jamy)
- From Seed to Snack – Popcorn.org
Comme j’ai dit, le maïs qui pousse dans un champ n’est probablement pas du maïs à pop-corn : son péricarpe (sa peau) ne retient pas la pression de l’eau au moment de chauffer et ne permet pas de former cette mousse ni le « pop ».
Il faut du maïs spécial, comme celui-ci ou celui-là (liens Amazon).
Inutile d’en acheter quinze paquets : une fois transformé en pop-corn, le gain de volume est d’un facteur 30 environ, ce qui en fait un snack particulièrement économique. Une casserole avec deux cuillères d’huile de cuisson (tournesol par exemple) et une seule poignée de grains de maïs, un petit fond donc, suffiront pour remplir la casserole de pop-corn à la fin ! Il ne restera alors plus qu’à sucrer, ou saler, et à déguster !
C’est quoi les mAh ? kWh ? C ?
Couleur science par Anonyme le 17/11/2022 à 04:34:00 - Favoriser (lu/non lu)

Pour les téléphones ou les batteries USB, les capacités de batterie sont exprimées milliampèresheure, ou mAh (ou l’ampèreheure, Ah). Pour les voitures électriques ou les batteries d’ordinateurs portables on utilise plutôt le kilowattheure, ou kWh (ou le wattheure, Wh).
Toutes les batteries servent à la même chose : stocker de l’énergie électrique, donc pourquoi cette distinction ? Quelle utilité ?
Pour répondre à la question rapidement : c’est une question d’échelle. Le kilowattheure est une grande unité : cela représente beaucoup d’énergie, beaucoup plus que ce que ne contient une batterie de téléphone. Si on exprimait les 2 500 mAh d’un téléphone en kWh, on aurait 0,012 kWh. Ça marche, mais c’est pas forcément facile à assimiler, et en tout cas pas bien vendeur.
Il a d’autres différences entre ces deux unités, notamment le fait important que le mAh ne soit pas une unité d’énergie !
Le kWh
Le kilowattheure (kWh, et non KWh, ni Kwh) est homogène à des joules et est bien une unité désignant une quantité d’énergie. Ici, elle concerne l’énergie emmagasinée dans une batterie, à priori une grosse batterie, comme celle d’une voiture électrique ou d’un PC portable.
C’est aussi en kWh que le fournisseur d’électricité décompte votre consommation électrique. Une voiture consommant tout de même une bonne quantité d’énergie pour vous transporter, il semble donc relativement commode d’utiliser les mêmes unités : cela permet de rapidement donner une idée du coût d’une recharge d’une voiture électrique, par exemple.
Ensuite, la puissance au sens large (pas seulement électrique) se traduit comme un débit d’énergie par unité de temps. En effet, des kilowattheures divisés par des heures sont des kilowatts, une puissance. Ainsi, un appareil d’une puissance de 10 kW qui tourne durant 2 heures, va consommer 10×2 = 20 kWh, tout simplement.
Le mAh
Si l’unité du wattheure (ou kilowattheure) est bien homogène à une énergie, les ampèreheures (ou milliampèreheures) ne le sont pas.
L’ampèreheure est homogène au coulomb, qui est l’unité de la quantité de charge électrique.
Une batterie comportant une certaine quantité de charges peut se décharger plus ou moins vite. Une batterie de 1 Ah peut ainsi faire circuler un courant de 1 A pendant une heure. Ou bien 0,5 A pendant deux heures, ou bien 0,25 A pendant 4 heures, etc.
L’ampère lui-même correspond à l’intensité d’un courant électrique qui fait passer une charge d’un coulomb en une seconde. L’intensité peut donc être exprimée en coulomb par seconde. En multipliant des ampères par des heures, on retombe donc sur des coulombs, soit une charge, pas une énergie.
L’ampère, qui est l’unité de l’intensité du courant électrique peut alors être vu comme un débit de charges électrique : l’intensité d’un courant est un débit.
Le mAh est une unité utile pour savoir combien de temps votre batterie va — théoriquement — pouvoir faire fonctionner un appareil donné. La durée va uniquement dépendre du courant débité.
Il n’est pas question d’énergie ici, seulement de quantité de charges et de durée d’utilisation.
Alors mAh ou kWh ?
Dans ce qui précède, on arrive à noter un certain parallèle :
- les watt ou les kilowatts, la puissance, sont un débit d’énergie par unité de temps.
- les ampères ou les milliampères, l’intensité, sont un débit de charges par unité de temps.
Dans les deux cas on peut tout à fait parler d’un débit (d’énergie ou de charge). Si l’on multiplie ce débit par un temps, on retombe sur la quantité initiale (énergie ou charge). Et c’est ce que l’on fait quand on utilise ces unités, et c’est pour ça que l’on rajoute le « h » sur les kW et les mA, qui nous donnent alors les kWh ou les mAh.
Si l’on se souvient, les watts (W) électriques sont la puissance d’un appareil électrique. Ce dernier correspond à la tension nominale multipliée par l’intensité du courant qui le traverse. Ainsi, l’énergie consommée est également au produit de la tension, de l’intensité et de la durée d’utilisation de l’appareil.
Si l’on veut obtenir l’énergie consommée à partir d’une valeur en mAh, c’est-à-dire une intensité et une durée, il faudra en plus multiplier par une tension.
La plupart des téléphones ou les autres petits appareils électriques à batterie (oreillettes, consoles, montres…) utilisent des batteries Li-Ion à une seule cellule, avec une quantité de charge variable mais délivrant une tension identique de 3,7 V.
Ainsi, on pourra convertir une valeur exprimée en mAh en kWh, mais en tenant compte de la tension.
Ceci est important, car une batterie qui délivre un courant donné pendant une durée donnée avec une tension élevée aura plus d’énergie que la batterie qui délivre le même courant pendant la même durée, mais avec une tension plus faible.
Par exemple :
- 1 cellule Li-Ion de 1 000 mAh produisant 3,7 V a une énergie de 3,7 V × 1 000 mA × 1 h = 3,7 Wh ;
- 1 cellule NiMH de 1 000 mAh produisant 1,5 V aura une énergie de 1,5 V × 1 000 mA × 1 h = 1,5 Wh.
Ici, à quantité de charges égales, la puissance d’une cellule Li-Ion est plus importante qu’une cellule NiMH, et l’énergie qu’elle stocke également, même si les deux contiennent la même charge électrique. La différence est alors que la batterie au lithium (Li-ion) débite cette charge avec plus de puissance, plus de force que la batterie au nickel (NiMH).
Le « C »
Dans le cadre des batteries pour le modélisme telle que ceux pour les mini-drônes, on parle également de « C » : 10C, 30C, 45C…
Ce facteur C permet de calculer l’intensité maximale (et donc la puissance) que la batterie peut fournir.
En effet, comme expliqué ci-dessus, une batterie de 1 000 mAh peut produire 1 000 mA durant 1 h, ou bien 500 mA durant 2 h, etc. Mais si on veut, on peut aussi calculer dans l’autre sens : produire 2 000 mA durant 30 minutes, 4 000 mA durant 15 minutes, etc.
Si on va plus loin, on peut alors trouver 1 000 000 mAh durant 1/1 000 d’heure (soit 3,6 secondes). C’est possible ? Non, pas vraiment. La réaction chimique qui produit le courant électrique à l’intérieur d’une batterie n’est pas infiniment rapide : elle est limitante quant à l’intensité qui peut en sortir. Pour une batterie Li-ion de base, on ne pourra que rarement dépasser 10 A.
C’est là qu’intervient le facteur « C ». Ce facteur indique quelle intensité maximale la batterie peut produire. Ce facteur est à multiplier par la valeur de la capacité en mAh de la batterie.
Ainsi, une batterie de 2 000 mAh de 10 C pourra produire 2 000 × 10 = 20 000 mA, soit 20 ampères. Notons qu’ici on bafoue totalement les unités, et qu’on passe de milliampères-heure à des ampères (sauf à considérer que le C est homogène à l’inverse d’une durée). Cette même batterie avec 40 C pourrait produire 2 Ah × 40 = 80 ampères, mais sont autonomie serai bien moindre). On arrive à faire cela en réduisant la résistance interne des batteries.
À capacité égale, une batterie avec un C plus gros produira plus de puissance (les moteurs de votre drone tourneront plus vite) mais donc moins longtemps.
Conclusion
Wh et Ah ne sont donc pas la même chose, mais on arrive tout de même à obtenir une correspondance entre les deux.
Quand utilise-t-on l’un ou l’autre ?
Cela dépend de l’usage. Le mAh est plus adapté à la compréhension et au marketing : « 2 500 » ou « 3 000 », ça parle déjà davantage dans une fiche produit que 0,012 ou 0,015 kWh. On aurait pu utiliser également les Wh, mais l’industrie est restée sur les milliampèresheure, comme elle est restée sur les tailles d’écran en pouces plutôt que des mètres.
Le kWh est lui resté sur les batteries plus grosses : certaines batteries externes comportent les inscriptions en Wh/kWh et en mAh/Ah, ainsi que les batteries énormes des voitures électriques, où personne ne parlerait jamais de mAh.
Le C quant à lui n’a pas grand chose à voir avec la capacité électrique d’une batterie, mais donne plutôt une indication sur sa puissance, et son intensité maximale qu’elle peut produire, à tension fixe.
À quoi correspondent les orbitales électronique ? Et les nombres quantiques ?
Couleur science par Anonyme le 03/11/2022 à 05:45:00 - Favoriser (lu/non lu)

À l’école, en chimie, on apprend que les atomes sont composés d’un noyau avec des électrons qui tournent autour, organisés en couches électroniques.
Naturellement, on pense alors à une organisation sous la forme de cercles comme des planètes autour d’une étoile. Ce modèle est intuitif et facile à se représenter, mais il ne correspond pas à la réalité, car il n’explique pas tout.
Si vous jetez un œil à un manuel de chimie un peu plus avancé, vous verrez plutôt des orbitales atomiques avec des formes très étranges :

D’où viennent ces choses ? Que voit-on ici ? Pourquoi ces formes étranges ?
Rappel de physique quantique et des électrons
Incertitude
Loin du modèle planétaire d’un atome où les électrons font figure d’une petite bille électrique qui gravite autour d’un noyau atomique, on admet aujourd’hui que le modèle d’un atome est celui d’un noyau avec un nuage d’électrons autour. L’idée de « nuage » désigne ici quelque chose de fluide, de flou, donc tout le contraire d’une couche circulaire ou sphérique contenant des billes.
Ce nuage ne se contente pas de contenir l’électron : il est l’électron.
Ce modèle est lié à l’hypothèse selon laquelle l’électron n’a pas une position bien définie, et provient de la notion d’incertitude de Heisenberg sur la position et la vitesse d’une particule (qui ne peuvent être connus simultanément de façon précise).
À la place d’une position et d’une trajectoire, donc, on associe à l’électron une probabilité de présence. Cela signifie qu’à chaque endroit donné de l’espace, on a une probabilité précise de trouver l’électron que l’on recherche.
On peut alors définir des zones de l’espace dans laquelle l’électron se trouve avec une probabilité arbitrairement choisie, typiquement 90 %.
L’idée derrière le calcul des orbitales les nuages électroniques, c’est ça : délimiter la région de l’espace tel qu’on ait 90 % de chance d’y trouver l’électron. Le reste de l’univers tout entier constituant les 10 % restants.
Ces « régions », telles que je les appelle, ce sont les orbitales atomiques.
Dualité onde-particule, fonction d’onde
Une autre notion très importante en quantique, c’est la nature même de la matière ou de la lumière. Historiquement, ce que Newton avait considéré comme des « billes de lumière », les photons, pouvait aussi manifester des comportements ondulatoires, telle que des interférences. Pendant très longtemps, le débat de savoir si un photon était une onde ou une particule divisait la communauté scientifique. Le problème a pu être plus ou moins résolu grâce à la physique quantique, en proposant un objet mathématique dont la nature était particulaire et ondulatoire à la fois.
L’électron — comme le photon — présente également un caractère ondulatoire selon les cas de figure. Cela ne veut pas dire que le caractère corpusculaire a disparu : les deux sont là.
Cette « onde-particule » est appelée en physique quantique un paquet d’onde, et constitue le modèle d’une entité qui possède à la fois le caractère d’une onde et celui d’une particule.
On peut donc voir l’électron non comme une bille orbitant un atome, mais telle une onde évoluant autour d’un noyau atomique, comme recourbée sur elle-même.
Si l’on donne plus ou moins d’énergie à l’électron, l’onde qui lui est associée va vibrer plus rapidement et va occuper une orbite avec une forme différente. Les différents modes de vibration correspondent alors à différentes harmoniques de cette onde.
La détermination de ces harmoniques et la forme de l’onde qui en résulte se fait par le calcul de la fonction d’onde associée à l’électron. Cette fonction s’obtient en résolvant l’équation de Schrödinger, très célèbre, et permet de calculer la probabilité de présence de l’électron en tout point de l’espace.
Juste pour vous mettre en appétit, voici à quoi ressemble la fonction d’onde pour l’atome d’hydrogène. L’hydrogène a bien un seul électron, mais ce dernier peut être dans une orbitale ou une autre, selon son énergie :
$$\Psi_{n\ell m}(r, v, \phi) = \sqrt{\left(\frac{2}{na_0}\right)^3 \frac{(n-\ell-1)!}{2n[(n+\ell)!]}} e^{-\frac{\rho}{2}}\rho^\ell L^{2\ell+1}_{n-\ell-1}(\rho) \sdot Y_{\ell m}(v, \phi)$$
Orbitales atomiques
Maintenant combinons ces deux notions : d’une part, on définit des régions de l’espace où l’onde a une probabilité arbitraire de se trouver (90 %), et d’autre part, l’électron qui évolue de façon ondulatoire au sein de cette région, et dont le mode de vibration dépend de son énergie.
Tout système oscillant décrit des formes plus ou moins géométriques, à cause de ses modes de fréquence propre[1]. L’oscillation d’un électron au sein d’un atome n’y déroge pas, et en appliquant la fonction d’onde à un électron, on obtient la forme de ses différentes orbitales, correspondant chacune à un niveau d’énergie.
C’est la géométrie de ces orbitales que l’on voit sur ces images.
Les niveaux d’énergie sont définis de façon formelle par quatre grandeurs : les quatre nombres quantiques de l’électron. Ces nombres quantiques suffisent et permettent de décrire une orbitale électronique au sein d’un atome.
Chaque nombre apporte, de façon simplifiée, une information à propos de l’orbitale : le premier nombre peut être associé à sa taille, le seconde sa forme, le troisième son orientation dans l’espace, le quatrième le sens de rotation de l’électron.
Ces nombres sont quantifiés (discontinus) : les modes de vibration associées à chaque électron le sont également, et c’est pour cette raison que les orbitales ont des formes si régulières et délimitées.
Pour le moment, commençons par voir les quatre nombres quantiques, qui est le but de cet article.
Les nombres quantiques
Les électrons s’organisent en couches, sous-couches et orbitale au sein d’un atome. La découverte de cette organisation s’est faite par étape au cours du XXᵉ siècle. Toutes les notations empiriques qui y réfèrent sont empreints de cette histoire et réfèrent souvent, comme on va le voir, à l’analyse spectrale, qui est la méthode ayant permise la plupart des découvertes.
Dans ce qui suit, je vais retracer le cheminement historique. Je ferais aussi le lien entre les notations empiriques et les notations modernes.
n : le nombre quantique principal, ou couche électronique
Historiquement, on a remarqué que certains éléments pouvaient être regroupés selon leurs propriétés chimiques. Le potassium et le sodium par exemple, ou encore le fluor, le chlore et le brome : à chaque fois ils avaient des propriétés très proches et formaient des molécules similaires.
Bohr a proposé dès 1913 un modèle atomique où les électrons s’organisaient en couches distinctes : le modèle de Bohr de l’atome :
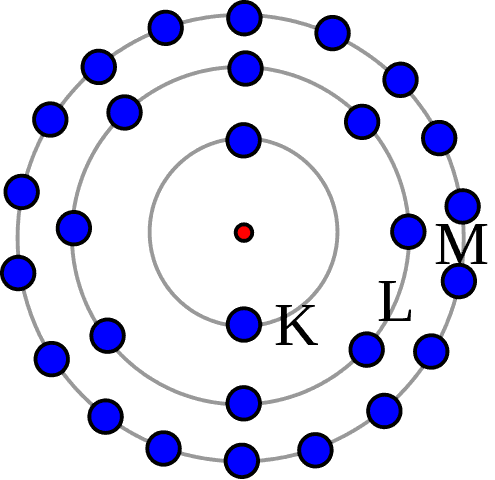
Ici, seules les couches externes servaient à la chimie, indépendamment des couches internes. Les couches externes avec un même nombre d’électrons conféraient alors les mêmes propriétés chimiques aux éléments, d’où leur classement dans la même colonne au sein du tableau périodique.
Ces différentes couches d’électrons étaient appelées K, L, M, N… etc. jusqu’à Q pour le tableau périodique actuel. Cette dénomination provient des premières expériences utilisées en spectroscopie des rayons X[2].
Aujourd’hui, pour la couche électronique, on parle plutôt du nombre quantique principal, noté « n ». n est numéroté de n=1 pour (K) la première couche, n=2 pour (L) la seconde, n=3 pour (M) la troisième, et ainsi de suite.
Les couches électroniques correspondent à une énergie grandissante, qui se traduit par un éloignement croissant de l’électron à son noyau.
Pour l’instant, je crois que ça n’est pas encore trop compliqué. Ajoutons juste que chaque couche électronique peut contenir un nombre d’électrons égal à 2n², au maximum.
Pour les 4 premières couches, on a donc :
| n | nombre d’électrons maximal par couche |
|---|---|
| 1 | 2 |
| 2 | 8 |
| 3 | 18 |
| 4 | 32 |
| … | … |
| n | 2n² |
Dans le tableau périodique, hormis pour les éléments de transition (le bloc central), la couche électronique externe d’un atome est appelée couche de valence. C’est la couche qui détermine les propriétés chimiques de l’atome.
ℓ : le nombre quantique secondaire (ou azimutal), sous-couche électronique
Découverte
En analysant le modèle de Bohr, on s’aperçoit que ce n’est pas encore très précis. En effet, plusieurs dizaines d’électrons peuvent être sur la même orbite (c’est à dire avec la même énergie). Or, lorsque l’on observe les raies spectrales produites par les atomes, on voit beaucoup plus de transitions que de couches électroniques. Il devait y avoir une structure interne à chaque couche : ce sont les sous-couches.
C’est Sommerfeld qui proposa sa solution, en proposant de nouveaux nombres quantiques. Dans le modèle de Sommerfeld-Bohr, les sous-couches peuvent avoir des formes elliptiques autour d’une même couche circulaire (donc avec le même n).
L’hypothèse d’une sous-structure propre à chaque couche a donc été mise sur la table dans ce modèle, et on lui associe le second nombre quantique, ℓ, le nombre quantique azimutal.
ℓ réfère à la grande lettre L utilisée en mécanique pour décrire le moment cinétique (ou moment angulaire), une grandeur physique qui apparaît dans le cas de masses en rotations. L’électron étant en rotation autour du noyau, il dispose d’un moment cinétique : cette lettre est donc restée. Dans le cas de l’électron, le moment cinétique est quantifié.
Là où le nombre quantique principal était plutôt associé à la taille d’une couche, le nombre quantique azimutal lui donne sa forme. Dans le modèle de Sommerfeld, c’est un peu le degré d’aplatissement de la couche électronique :

Aujourd’hui, le modèle circulaire/elliptique est abandonné, et on utilise des représentations en formes de lobes.
Description et représentation moderne
Quantitativement, chaque couche électronique n est divisée en n sous-couches, numérotées de 0 à n−1. Par exemple, la couche n=3 aura les sous-couches ℓ=0, ℓ=1 et ℓ=2. Chaque sous-couche ℓ peut contenir jusqu’à 2(2ℓ+1) électrons.
Comme je l’ai dit, ces sous-couches électroniques ont été découvertes par l’analyse des spectres d’émission des atomes, et donc des raies. Or, on distinguait les raies selon leur « importance » dans le spectre. Ces raies ont été nommées avec des qualificatifs (en anglais).
Les quatre premières sous-couches portent donc pour nom les qualificatifs suivants :
- ℓ=0 : s (pour sharp)
- ℓ=1 : p (pour principal)
- ℓ=2 : d (pour diffuse)
- ℓ=3 : f (pour fundamental)
Les fameux « s, p, d, f » viennent donc de là, et ils correspondent tout simplement aux sous-couches 0, 1, 2, 3. La sous-couche « s », est présente dès la première couche. La sous-couche « f » n’est présente que dès la couche n=4.
Quant aux ℓ suivants, non découvertes dans la nature, on suit simplement l’ordre alphabétique (sans le i, jugé trop ressemblant au j) :
- ℓ=4 : g
- ℓ=5 : h
- ℓ=6 : j
- ℓ=7 : k
- …
On peut résumer les deux premiers nombres quantiques dans le tableau suivant :
| couche | sous-couche | |||
|---|---|---|---|---|
| n | 2n² | ℓ | nℓ | 2(2ℓ+1) |
| 1 (K) |
2 | 0 | 1s | 2 |
| 2 (L) |
8 | 0 | 2s | 2 |
| 1 | 2p | 6 | ||
| 3 (M) |
18 | 0 | 3s | 2 |
| 1 | 3p | 6 | ||
| 2 | 3d | 10 | ||
| 4 (N) |
32 | 0 | 4s | 2 |
| 1 | 4p | 6 | ||
| 2 | 4d | 10 | ||
| 3 | 4f | 14 | ||
| … | … | … | … | … |
Attention car n est numéroté en commençant à 1, mais ℓ est numéroté en commençant à 0. D’où, la relation suivante parfois rencontrée :
$$0 \leqslant \ell \leqslant n-1$$
Si, schématiquement, les couches successives sont de plus en plus grandes en taille, les multiples sous-couches ℓ correspondent à des « portions » de ces couches et avec des formes bien définies.
Voyons tout ça.
Sous couche « s » (ℓ=0)
Comme expliqué en introduction, les formes des sous-couches répondent aux solutions de la fonction d’onde. Si l’on trace cette fonction pour les sous-couches s (1s, sous-couche s de la couche 1 ; 2s, sous-couche s de la couche 2 ; 3s, sous-couche s de la couche 3), on obtient ceci :
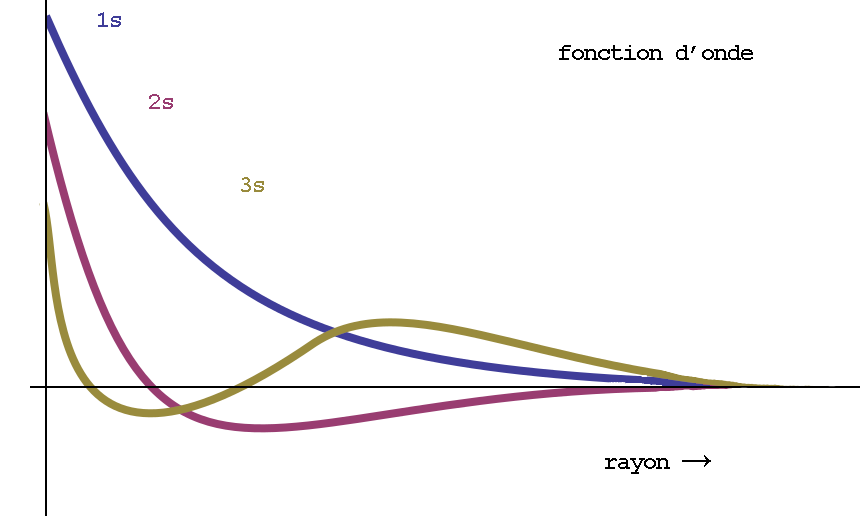
Cette courbe traduit la probabilité (en y) de trouver un électron en fonction de la distance au noyau (en x). On voit que pour 1s, il y a un seul lobe positif et décroissant : il y a donc une zone où la probabilité est très forte autour du noyau. En trois dimensions, cela correspond à une sphère centrée sur le noyau.
Pour la 2s, on voit qu’il y a deux lobes : un positif au début (la partie de la courbe au dessus de l’axe horizontal), et un négatif après un moment (la partie de la courbe en dessous de l’axe) qui remonte ensuite vers 0. On a donc deux sphères concentriques. Vu que la courbe 2s franchit l’axe des abscisses, et passe par 0, cela signifie qu’entre les deux sphères, il y a une zone où la probabilité de trouver un électron 2s est nulle. Pour 3s enfin, il y a 3 lobes et deux passages par 0 : on a donc trois sphères distinctes.
Si l’on représente ça en trois dimensions, on obtient ceci :

Sous couche « p » (ℓ=1)
Regardons maintenant les sous-couches p (donc ℓ=1). Cette sous-couche n’apparaît qu’à partir de la seconde couche. On peut tracer les fonctions d’ondes :
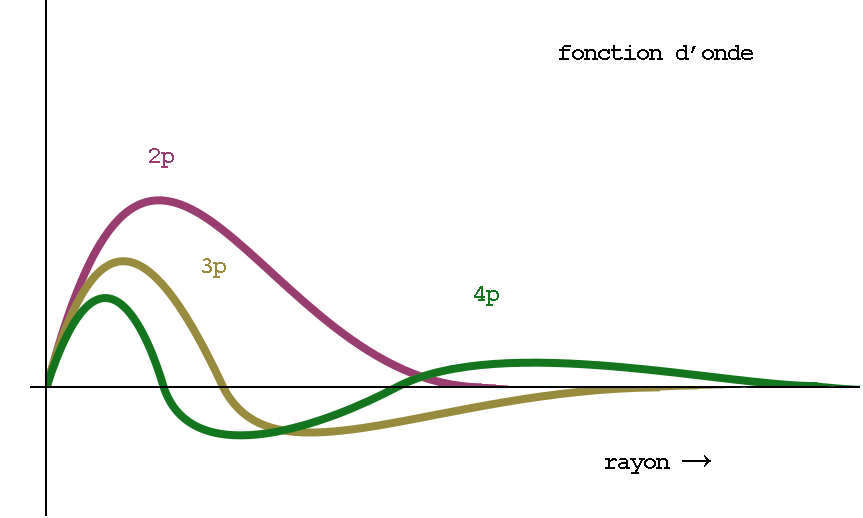
Ici, on remarque qu’au niveau de l’origine, donc proche du noyau, la probabilité est nulle. Les lobes n’englobent donc pas le noyau. Il faut s’en éloigner un peu pour commencer à avoir une chance de trouver un électron. Ce qu’il faut voir ici, c’est que la courbe est symétrique de l’autre côté de l’origine, dans les rayons négatifs si l’on veut. Physiquement, cela correspond à une composante dépendante de l’angle à laquelle on se trouve par rapport au noyau.
Cette sous-couche p possède donc deux lobes hémisphériques de part et d’autre du noyau, et ça au sein de chaque couche :
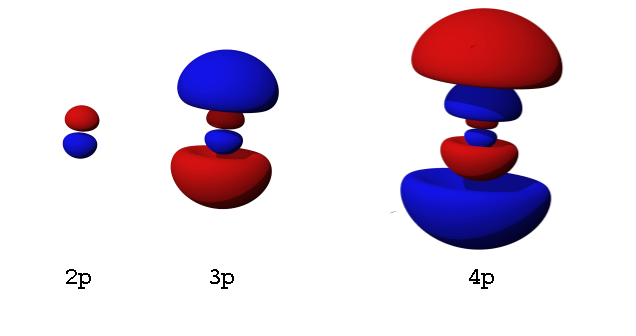
Les couleurs aident à visualiser les différents lobes, mais ils représentent mathématique le signe (+/−) de la fonction d’onde, et physiquement sa phase (car la composante ondulatoire confère à l’électron une fréquence, une amplitude et une phase).
Sous couche « d » (ℓ=2)
Si l’on poursuit maintenant, on arrive sur les sous-couches d (ℓ=2).
Ces sous-couches d sont en forme de trèfles ou de donut (l’un ou l’autre dépendant du troisième nombre quantique, mℓ, que l’on va voir juste après).
Le principe est fondamentalement le même. Ici, la fonction d’onde est encore plus dépendante de l’angle et les lobes figurent donc un peu partout autour du noyau :
À nouveau, à chaque fois qu’on progresse dans les couches, les sous-couches d sont de plus en plus lobées :

Sous-couche « f » et suivante (ℓ=3, 4, 5…)
De façon similaire, les sous-couches f, g, et suivantes ont des formes encore plus lobées et exotiques.
mℓ : le troisième nombre quantique, ou nombre quantique magnétique, de l’orbitale électronique
Découverte
Si vous avez suivi : n correspond à la couche, ℓ à la sous-couche, les « ellipses » de Sommerfeld. Bien qu’un cercle reste identique quelque soit son orientation, une ellipse peut être orientée : vers la droite, vers la gauche… Sommerfeld proposa donc également un troisième nombre quantique, destiné à définir l’orientation considérée de son ellipse.
Chaque sous-couche désigne donc un ensemble d’orbitales de même forme, mais avec des orientations différentes.
Maintenant, souvenez-vous : à une transition électronique correspond une raie dans le spectre d’émission. Ceci est vrai en temps normal. Mais en temps anormal, c’est à dire ici, dans un champ magnétique, on s’est rendu compte que les atomes produisaient des raie multipliée en plusieurs sous-raies.
Sans le champ magnétique, plusieurs raies se superposent car elles ont la même énergie. C’est normal : les ellipses de Sommerfeld ont la même forme. Mais dans un champ magnétique, l’orientation de l’ellipse a également une influence sur la couleur ! Le champ magnétique lève la superposition : on passe donc d’une raie à une multitude de raies contigües[3] :
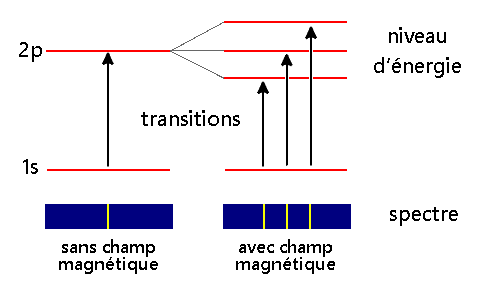
Ici, on parle d’une orbitale, chacun avec son orientation propre (X, Y, Z…). Les orbitales avec la même forme se regroupent en sous-couche (les ellipses). Et les différentes sous-couches en couche (les ellipses étant centrées autour d’un cercle).
Si le champ magnétique lève cette superposition (on parle de levée de dégénérescence), l’orientation du champ magnétique a une influence sur les transitions électroniques : les électrons dans les orbitales alignés sont moins énergique que les électrons qui sont dans l’autre sens. Cela se traduit par un petit décalage de la raie spectrale correspondante et elles ne se superposent plus exactement.
Ce troisième nombre quantique, introduit par Sommerfeld et destiné à donner l’orientation de l’orbitale est nommé le nombre quantique magnétique, en référence au phénomène qui le met en évidence. Le nombre quantique magnétique est noté m ou mℓ.
Description et représentation moderne
Chaque sous-couche électronique ℓ peut contenir 2ℓ+1 orbitales, numérotées de −ℓ à +ℓ. Donc la sous-couche f (ℓ=3) aura sept orbitales mℓ : −3, −2, −1, 0, +1, +2 et +3.
Les orbitales sont des versions « orientées » des sous-couches. Ce que l’on représente un peu plus haut comme une paire de lobes est une orbitale, et plusieurs orbitales de même forme mais orientés différemment forme une seule sous-couche.
Typiquement, dans le cas des sous-couches p avec deux lobes, ces derniers peuvent être alignés selon l’axe X, Y et Z :

Ces orbitales coexistent de façon superposée, si l’atome a suffisamment d’électrons, bien entendu. Elles ont la même énergie, et seul le champ magnétique (ou électrique) peut les mettre en évidence et levant la superposition des raies spectrales.
Dans les sous-couches d, f et suivantes, qui sont plus complexes, on peut avoir d’autres orientations : XY, XZ, YZ, X²… Un peu comme on peut avoir des directions « sud », « sud-ouest », ou « sud-sud-ouest » entre les points cardinaux principaux. On obtient alors des orbitales aux figures très diverses en résolvant la fonction d’onde :

Notons que parfois, on a des représentations multicolores (comme dans l’introduction de l’article). La raison est purement mathématique : il faut savoir que la fonction d’onde se résout dans le cadre des nombres complexes. Les images en bleu/rouge ici sont des projections dans les nombres réels. Celles avec les couleurs montrent la même chose mais sans privilégier une projection particulière dans l’espace des réels. Les couleurs représentent alors les valeurs de mℓ (ou eigenstate), et cela reste bien entendu une simple représentation (les électrons n’ont pas de couleur).
Entre ceux deux types de représentations on trouve la correspondance assez facilement :

Voilà pour la description physique de mℓ.
On a vu les couches (K, L, M… pour n=1, 2,3), les sous-couches (s, p, d, f pour m=0, 1, 2, 3), les orbitales (avec mℓ=−2, −1, 0, +1…). Il manque un dernier nombre quantique. Pour ça, il faut constater que chacune des orbitales peut porter deux électrons au maximum : chacun de ces deux orbitales est alors différentié par ce quatrième nombre quantique : le spin.
ms : le quatrième nombre quantique, ou nombre quantique magnétique de spin
Le nombre quantique magnétique de spin, ou tout simplement spin est le dernier des quatre nombre quantique qui définit un électron.
Il est souvent dépeint comme le sens de rotation d’un électron, mais ce dernier étant ponctuel, cette analogie n’a pas de sens physique. On peut néanmoins l’assimiler à un moment cinétique intrinsèque à l’électron : celui-ci étant chargé électriquement, le moment cinétique lui donne un moment magnétique, qui peut être positif ou négatif.
Toutes les particules peuvent se voir associer un nombre quantique de spin.. Au sein d’un atome, l’électron peut prendre deux valeurs possibles : +1/2 et −1/2, reflétant la direction selon laquelle est dirigée son moment magnétique.
La découverte du spin n’est pour une fois pas liée à la spectroscopie, mais au magnétisme, au cours de l’expérience de Stern et Gerlach de 1922.
Ces derniers ont utilisé des atomes d’argent en phase vapeur, qu’ils ont accéléré à travers une fente. Là, de l’autre côté de la fente, on a placé un écran. Naturellement, il s’est formé sur cet écran une ligne d’argent correspondant aux atomes qui traversent la fente. Jusque-là rien d’anormal.
Ensuite, ils ont placé un champ magnétique à la sortie de la fente sur la trajectoire des atomes d’argent. Ils voulaient voir si le moment magnétique était quantifié et s’attendaient donc à voir autant de lignes d’argent que d’orbitales mℓ, donc forcément un nombre impair.
Ce qu’ils observaient était que le faisceau s’est scindé en deux : un en haut et un en bas. Comment expliquer ça ?
Le moment magnétique n’explique pas seul ce résultat. Les physiciens ont dû admettre qu’il fallait introduire un nouveau nombre quantique lié au magnétisme. Ils ont donc proposé ms, le nombre magnétique de spin.
Qu’en conclure ?
Un électron est chargé électriquement. Si on le met en déplacement, on obtient un champ magnétique. Ce champ va réagir à tout autre champ magnétique présent. À présent, si l’on place ces électrons au sein d’un atome, ils s’organisent et leur énergie prennent des valeurs quantifiées, y compris le spin. Normalement, la somme des spins de tous les électrons est nulle (car les +1/2 et −1/2 s’annulent deux par deux).
Pas dans l’atome d’argent, et les autres atomes dont la couche de valence contient un électron seul (or, cuivre, sodium…) : ici, le dernier électron se trouve seul sur sa couche de valence et son spin n’est pas annulé. L’atome dans son ensemble, bien qu’ayant une charge électrique nulle, maintient un moment magnétique à cause de cet électron. L’atome agit alors comme un tout petit aimant.
Lorsqu’on accélère cet atome à travers un champ magnétique, il va être dévié, soit en haut, soit en bas, en fonction de son spin et on obtient deux lignes d’argent plutôt qu’une sur l’écran :

On distingue donc, au sein de chaque orbitale, deux électrons avec des spins opposés. Deux est le nombre d’électrons que chaque orbitale peut contenir.
Configuration électronique globale d’un atome
Dans tous ce qui précède, on a discuté des orbitales atomiques, c’est-à-dire des zones de probabilité de présence des électrons en fonction de leur nombre quantique.
Ces orbitales sont généralement montrées individuellement, mais il faut comprendre qu’elles sont toutes là autour du noyau. L’atome d’or, par exemple, possède 79 électrons. La représentation de cet atome dans son état le plus stable est donc la superposition de 40 d’orbitales (39 avec deux électrons, plus une avec un électron célibataire).
Maintenant, comment savoir quelles orbitales sont occupées ? Dans quel ordre sont remplies les orbitales atomiques ? Comment est assemblé cet atome ? Il a été découvert que le remplissage des orbitales électroniques n’était pas aléatoire : les électrons vont toujours se placer dans certaines orbitales avant de se placer dans d’autres.
Tout ce manège obéit à des règles que des scientifiques on pu découvrir en observant le comportement des atomes :
- la règle de Klechkowski
- la première règle de Hund
- le principe d’exclusion de Pauli
D’un point de vue pratique, ces règles gouvernent les positions et expliquent les propriétés des éléments dans le tableau périodique, par exemple :

Tout ceci sera l’objet d’un éventuel prochain article, mais on peut déjà dire que de façon générale, les atomes cherchent à se mettre dans une configuration la plus stable et la moins énergétique possible. En termes d’orbitales, cela se traduit par un remplissage préférentiel des couches électroniques proches du noyau avant de remplir les couches plus éloignées, donc un remplissage par n croissant : la couche K (n=1) est remplie avant la couche L (n=1), elle-même avant la couche M (n=2), etc.
Je dis bien « de façon générale », car ceci n’est vrai que pour le début du tableau périodique. De plus, comme toute règle, il y a des exceptions. Effectivement, certains atomes peuvent être plus stables si on entame certaines couches externes avant de compléter les couches internes.
Enfin, toutes ces orbitales ne sont valable que pour des atomes isolés. Quand on a à faire à des molécules, il y a la formation d’une toute autre structure des nuages électroniques, appelées orbitales moléculaires.
Conclusion
Cet article est long, et complexe. C’est normal : il tente d’expliquer en une seule fois un sujet très compliqué de physique quantique. J’espère néanmoins qu’il a pu aider à comprendre un peu comment sont formés les atomes.
Il faut bien comprendre que tout ceci correspond au modèle actuel de l’atome : celui résultant de la fonction d’onde, obtenue pour un atome donné par la résolution de l’équation de Schrödinger.
La découverte de la structure d’un atome, ainsi que la mise au point de l’équation de Schrödinger ainsi que la fonction d’onde ne s’est pas faite en un jour. Il a fallu des décennies de travaux à un grand nombre de scientifiques aujourd’hui très connus : Rutherford, Bohr, Einstein, Sommerfeld, Schrödinger… pour ce ne citer qu’eux.
Leur travaux ont permis de révéler, petit à petit, la structure d’un atome et l’organisation des électrons partout autour. Du modèle de Rutherford, puis celui de Bohr, à celui de Sommerfeld et ainsi de suite jusqu’au modèle actuel avec les orbitales colorées présentées ici.
Dans mon article, j’ai essayé de conserver la chronologie et les idées que ces grands noms ont utilisés pour expliquer leurs découvertes (orbites circulaires pour Bohr, ellipses pour Sommerfeld, etc.), bien que ces idées et représentations ne soient plus d’usage de nos jours. J’ai également lié ces idées obsolètes à leur contreparties modernes, afin de bien comprendre ce qui se passe. J’espère que c’est le cas : c’est un article compliqué mais que j’avais envie d’écrire depuis longtemps.
Notes
- [1] Comme les plaques de Chladni ou les figures de Lissajous avec un double-pendule.
- [2] Fluorescence X et dénomination K, L, M… des couches électroniques
- [3] Cette « désuperposition » est appelée la levée de dégénérescence des états quantiques. Lorsque cette levée de dégénérescence de l’électron est faite au moyen d’un champ magnétique, on appelle ça l’effet Zeeman, et son analogue avec un champ électrique est l’effet Stark.
Références
Quantum number - Wikipedia
Quantum Numbers and Electron Configurations
The Shape of Orbitals - Quantum Numbers
Who discovered quantum numbers? - Quora
ChemTeam: Quantum Numbers
Ces Tweets de Brusicor02
S P D F orbitals Explained - 4 Quantum Numbers, Electron Configuration, & Orbital Diagrams
Ah, la science… (15)
Couleur science par Anonyme le 20/10/2022 à 04:52:00 - Favoriser (lu/non lu)

Cela faisait longtemps que le dernier article « Ah, la science » était sortie. Alors en voici un avec, comme toujours, quelques chiffres scientifiques intéressants ou impressionnants sortis de leur contexte.
650 grammes
Il s’agit de la masse corporelle que l’on perd quotidiennement rien qu’en respirant.
En inspirant, on capte de l’oxygène (O2), et en expirant, on perd du dioxyde de carbone (CO2). La différence entre les deux, le carbone (C), est issue de notre nourriture et est ainsi perdu.
En sus, nous expirons également de la vapeur d’eau (H2O), dont les constituants viennent également de notre nourriture : les glucides et lipides étant essentiellement composés de carbone, d’hydrogène et d’oxygène.
La masse que l’on perd quand on « perd du poids » part essentiellement en CO2 par expiration. Le fait étant que l’on expire davantage de carbone que notre alimentation en apporte et notre corps perd de la masse. Ce sont les produits de la décomposition de ces glucides et lipides par l’activité des cellules de notre corps que l’on rejette.
Ceci est aidé par l’activité sportive : quand on pratique du sport, les muscles sont davantage sollicités et ont besoin de plus d’énergie libérées par l’oxydation des sucres et des graisses. Les produits de cette oxydation (dioxydes de carbone et eau) sont produits en plus grande quantités et l’on doit respirer beaucoup plus pour tout rejeter (d’où le fait qu’on respire bien plus quand on fait du sport).
À raison de 30 mg par expiration et 15 respirations par minute, cela représente environ un demi-kilo de matière, dont environ 290 grammes de carbone piégé dans 1 kg de CO2 (le O2 provient, lui, de l’air). Bien sûr, ce CO2 fait partie du cycle du carbone et n’est pas celui responsable du réchauffement climatique.
Cette masse perdue vient s’ajouter à la masse que l’on élimine quand on va aux toilettes, ainsi qu’à la masse perdue par la transpiration et la perte de peau morte ou de cheveux, qui se renouvellent également de façon constante.
(source)
40 000 000 000 000 000 000
Il s’agit d’une estimation du nombre de trous noirs dans l’univers visible.
On estime à plusieurs centaines de milliards le nombre de galaxies dans l’univers visible, et à plusieurs centaines de milliards également le nombre d’étoiles dans chaque galaxie. Certaines de ces étoiles finissent en trous noirs à la fin de leur vie (quand elles s’effondrent, et si elles sont assez massives). Le nombre total de trous noirs serait ainsi estimé à 40 milliards de milliards, et cela représente environ 1 % de toute la masse (baryonique, donc la masse normale) de l’univers visible.
(source)
7 800 bars
Une pression ici : il s’agit de la pression exercée par l’eau qui gèle.
La glace flotte sur l’eau : ceci provient du fait que la glace est moins dense que l’eau. Si une certaine quantité d’eau gèle, la glace obtenue occupe un volume plus grand. Si l’eau se trouve dans un tuyau de canalisation et gèle, l’expansion de la glace exerce une pression pouvant faire éclater les tuyaux, généralement de cuivre. La pression exercée lors de ce phénomène est incroyablement élevée et peut atteindre ainsi 7 800 bars.
C’est 7 fois la pression qui règne tout au fond des fosses Marianne, l’endroit le plus profond de l’océan Pacifique, ou encore 7,8 tonnes par centimètre carré.
L’eau liquide est composée de molécules désordonnées. Quand elle gèle, les molécules s’organisent en structure cristalline et pour l’eau, cette structure ordonnée occupe plus de volume que la structure liquide désordonnée. C’est quelque chose qui n’est pas très commun parmi les matériaux, et on l’appelle l’anomalie dilatométrique. Cette « anomalie » est partagée avec le gallium (un métal liquide à 29 °C) et le plutonium. Seule une poignée de matériaux la présentent.
Ainsi, lorsque l’on stocke ces matériaux, il faut faire attention au récipient et à la température. Pour l’eau, on ne stocke jamais une bouteille pleine au congélateur, surtout si elle est en verre. On fait aussi attention aux canalisations quand il gèle.
Plus surprenant, certains arbres peuvent également exploser quand il gèle très fort : l’eau qui gèle écarte les fibres du bois et fait violemment éclater l’arbre.
Pourquoi y a-t-il une norme ISO pour préparer du thé ?
Couleur science par Anonyme le 06/10/2022 à 06:16:00 - Favoriser (lu/non lu)

Certaines personnes se perdent parfois sur Wikipédia (et constatent qu’on finit toujours sur la page de la philosophie), d’autres parfois dans la liste des normes ISO étranges.
C’est ainsi qu’on peut découvrir la norme ISO 3103, intitulée Thé — Préparation d’une infusion en vue d’examens organoleptiques.
Cette norme décrit, à l’aide de schémas et de plans côtés, une méthode standardisée pour préparer du thé. Préparer. Du. Thé.
Oui, il s’agit d’une norme bien réelle et n’est pas une farce. Pourquoi une telle norme ?
Faut-il une norme pour du thé ?
La norme ISO 3103 peut prêter à sourire, mais il s’agit d’un travail sérieux. Elle est une transposition de la norme BS 6008:1980 de l’Institut Britannique des Standards (BSI), qui reçut d’ailleurs un prix IgNobel — une version parodique des prix Nobel — pour ce travail. L’idée des IgNobel est de récompenser les travaux scientifiques à première vue ridicules, mais à seconde vue intéressants. Et c’est un peu le cas ici, pour l’ISO 3103, mais aussi toutes les normes en général.
La norme ISO 3103 n’est peut-être pas la plus utilisée au monde, mais elle permet de mettre tout le monde d’accord pour ce qui est d’un thé, qui est un produit parfois utilisé lors de la réalisation de tests sensoriels et gustatifs, ou « examens organoleptiques » comme ils l’appellent.
Le but est d’éviter que ce genre tests sensoriels soient entachés d’erreurs si la coutume locale d’un institut de recherche fait du thé à sa façon. Un thé préparé au Japon n’est pas le même qu’un thé préparé au Maroc, par exemple, et tout ça peut poser problème au cours d’études scientifiques.
Pour mettre tout le monde d’accord, notamment sur le temps d’infusion ou la quantité de plante, cette norme fut créée.
On peut faire le parallèle avec les tests de vision des couleurs. Certains domaines d’activité exigent que les personnes perçoivent les couleurs de façon normale. On peut imaginer certains domaines (en cuisine, ou en œnologie, par exemple) où il faille des tests standardisés liés au goût et à l’odorat. Dans ces là, il faut des protocoles également standardisés pour tester les gens sur leur aptitude à distinguer les goûts. D’où ce genre de normes, qui met tout le monde d’accord sur la façon de préparer un thé « type ».
La norme n’est pas destinée à préparer une tasse de thé parfaite, mais plutôt un thé « contrôle », ou neutre. Pour une tasse de thé parfaite, on pourra prendre l’essai littéraire de George Orwell : « A Nice Cup Of Tea ».
Pourquoi tout normer ?
Ce qui est expliqué ci-dessus par « mettre tout le monde d’accord » est précisément le but de tous les organismes de standardisation. L’ISO, le CEI, l’Afnor, le Tüv et d’autres organismes servent à cela. Mettre tout le monde d’accord.
Vous en connaissez sûrement un petit nombre car il suffit de regarder sur un chargeur de PC pour voir leur logos :

L’ISO, dont l’acronyme signifie en français « organisation internationale de standardisation », sont ceux qui définissent les standards industriels à l’échelle internationale.
Un standard — ISO ou non — est juste une règle, une loi, destinée à l’industrie et que l’on peut même ne pas être obligé de suivre. On la suit seulement si on a besoin : satisfaire un client, par exemple.
Une norme permet de simplifier le travail de tout le monde : si plusieurs industriels respectent la même norme, cela permet et même garantir une forme d’interopérabilité entre les différents acteurs de l’industrie concernée.
Un exemple très simple : les prises de courant. On visualise très bien ce que c’est : les deux broches, phase et neutre, la fiche de terre… Pourtant rien n’empêche un industriel de positionner ces broches d’une autre façon.
Ainsi, la prise type « E/F » utilisée en France (norme CEI 60320) n’est pas la seule qui existe. Certains ont peut-être vu des prises de type G anglaise (standard BS 1363) ou encore des types J suisse (SEV 1011). Il en existe un paquet d’autres dans le monde, et tous ne sont pas compatibles entre-elles ! Ces différences subsistent de façon historique aujourd’hui à travers le monde.
Maintenant, à l’intérieur d’un même pays, les normes permettent une uniformité : si ces normes n’avaient pas été établies (par le CEI, l’ISO, le BSI, l’Afnor…) alors chaque fabriquant aurait pu faire une prise dédiée. Pire, chaque appareil aurait pu fonctionner avec un type de courant différent : alternatif, continu, 220 V, 150 V… Ça aurait été très difficile à gérer.
On se souviendra de l’époque où chaque téléphone avait son propre format de chargeur, n’est-ce pas ? Aujourd’hui, c’est la norme USB (IEC 62680) qui a été retenue par l’industrie, ou imposée par la législation (en Europe notamment) pour les téléphones portables et d’autres petits appareils. Depuis, les prises USB se retrouvent partout et on peut brancher n’importe quel câble et charger n’importe quel appareil dessus.
Le fait que les fabricants d’appareils en tout genre se mettent d’accord permet à tous de s’y retrouver. Les utilisateurs, mais aussi les fabricants d’accessoires : il suffit de respecter la norme USB et on sera certain que tous les téléphones accepteront vos câbles.
Certains standards ne sont pas légalement obligatoires et les constructeurs peuvent choisir de se mettre d’accord entre eux. Parfois en revanche, le respect de certains standards est imposé pour qu’un industriel puisse commercialiser son produit. C’est généralement pour tout ce qui concerne la sécurité, des ceintures de sécurité de voitures, aux extincteurs en passant par la disposition des issues de secours dans un bâtiment.
Maintenant il y a des standards pour à peu près tout : du format et des vitesses des disques durs (norme SATA), au format des photos pour les permis de conduire français (Afnor NFZ 12-010), en passant par la définition de la note de musique du La 440 Hz comme la note de référence dans le domaine musical (ISO 16) ou la taille d’un conteneur de transport de marchandises (ISO 6346), d’une balle de fusil de guerre (7.62×51mm NATO), ou d’une feuille de papier A4 (ISO 216).
Oui, c’est grâce à l’ISO que tous les musiciens utilisent le La 440 de référence : avant, chaque pays, chaque conservatoire avait sa note de référence. Rien qu’à Paris, la note référence a changé trois fois au XIXe siècle : 420 Hz en 1807, 430 Hz en 1829 puis 435 Hz en 1859. Ce dernier a été accepté par l’Autriche, mais pas l’Allemagne, qui préférait alors la note à 440 Hz depuis 1835, tout comme les américains depuis 1936, qui ont ensuite standardisé ça chez eux puis à l’ISO en 1975.
Le but n’est pas de rendre la vie compliquée à coup de restrictions, mais de rendre la vie plus simple en fournissant des spécifications techniques qui seront vouées à fonctionner à tous les coups. Si différents fournisseurs respectent la même norme, leurs produits fonctionneront ensemble sans tracas.
Conclusion
L’ISO permet de poser un cadre pour permet à l’industrie de fonctionner facilement, un peu comme les textes de loi d’un pays posent un cadre permettant à la société de fonctionner correctement.
L’industrie aujourd’hui n’aurait jamais pu être ce qu’elle est sans l’ISO ni le reste. Vous imaginez si chaque voiture avait son propre carburant unique ? Chaque marque de frigo sa propre prise ? Chaque télécommande son propre format de pile ?
Certaines normes pourraient encore naître (par exemple pour les formats de cartouches d’imprimante), et d’autres améliorées (il reste encore beaucoup de formats de piles électriques différentes), mais globalement on est pas mal.
Notons que pour les cartouches d’imprimante, par exemple, les industriels n’ont aucun intérêt économique à se voir imposer une norme… Comme j’ai dit : si le législateur ne l’impose pas, les normes sont utilisées seulement si les différents acteurs le veulent bien. Et tant qu’il n’y a pas d’accord entre les acteurs, rien ne se passera.
D’où vient l’efficience d’une chaudière à condensation ?
Couleur science par Anonyme le 15/09/2022 à 05:15:00 - Favoriser (lu/non lu)

On vend les chaudières à condensation comme une façon économe de se chauffer, c’est-à-dire plus économe qu'une chaudière traditionnelle. Cet article a pour but d'expliquer le mécanisme astucieux derrière les chaudières à condensation.
Principe d’un système de chauffage
Le principe de base d'un chauffage à combustible (donc non électrique) quel qu'il soit est simple : on brûle un combustible pour en récupérer la chaleur dégagée. Cela se fait soit directement (feu de camp), soit indirectement (poêle à bois : le bois brûle et chauffe le poêle, et le poêle chauffe l'air), soit encore plus indirectement par l'intermédiaire d'un fluide transporteur de chaleur, comme l'air ou l'eau.
Ce dernier cas est celui d'une chaudière au fioul ou au gaz : on brûle du gaz, qui permet de chauffer de l'eau, et l'eau ensuite circule dans les radiateurs, qui enfin chauffent l'air. L'eau est donc là pour transporter l'énergie thermique, les calories, de la chaudière vers les pièces à vivre. L'eau est donc appelé un fluide caloporteur, et elle acquière ses calories via des échangeurs thermiques.
Quand l'eau transmet ses calories au radiateur, elle va elle-même les perdre et refroidir. Entre l'eau qui sort de la chaudière (~65 °C) et l'eau qui y retourne (~40 °C), il y a donc une différence de température, d'une vingtaine de degrés idéalement.
L'eau retournant dans la chaudière ne doit pas être trop froide car sinon elle doit être chauffée davantage pour la réchauffer complètement. Si la baisse de température reste modérée, alors on peut réduire la puissance de chauffe de la chaudière et faire des économies.
Ce réglage fait, l'efficience énergétique d'un tel système dépend ensuite de l'efficacité des échanges de chaleur : du brûleur à gaz vers l'eau, puis de l'eau au radiateur, puis du radiateur vers l'air.
Le premier échange thermique est particulièrement important : en effet, chaque calorie qui n'est pas transféré au fluide caloporteur est est alors perdue et évacuée avec les gaz de combustion, dehors. On chauffe littéralement pour rien si de la chaleur se trouve être renvoyée dehors.
Cas d'une chaudière à condensation
Les chaudières à condensation sont la norme aujourd’hui car ils présentent un rendement meilleur que les chaudières d’une génération précédente. Elles réalisent cela avec plusieurs « astuces ».
Première astuce
Une des astuces que l'on peut mettre en en œuvre, c'est donc tenter de capter les calories qui sont encore présenter dans les gaz d'échappement.
L'idée est de faire passer l'eau qui revient vers la chaudière par un échangeur thermique qui traverse les gaz d'échappements encore chauds. Les calories des gaz d’échappement sont alors récupérées : l'eau est alors préchauffée et la chaudière à proprement parler peut réduire sa puissance pour atteindre la température de chauffe de l’eau : on réduit ainsi la consommation de gaz.
Une des conséquences de cette méthode c'est que si l'eau se réchauffe dans les gaz d'échappements, alors les gaz d'échappement, eux, se refroidissent. Or, ces derniers contiennent essentiellement de la vapeur d'eau et du dioxyde de carbone. L'eau, en se refroidissant un peu, va se condenser et goutter à la sortie du condenseur. L'appellation vient de là.

Seconde astuce
Avec la première astuce, on récupère une partie des calories des gaz de combustion directement dans l'eau du circuit de circulation des radiateurs. Malheureusement, toutes les calories ne peuvent pas être captés. L’eau qui revient des radiateurs pour repasser dans la chaudière n’est pas exactement froide : elle est encore à environ 40 °C. Si l’eau est trop proche de la température des gaz, alors elle n’en capturera pas les calories. Pire, les gaz ne ne peuvent pas chauffer de l'eau qui dépasse leur propre température, et qui plus est, plus la différence de température est réduite, plus l'efficacité de l'échangeur thermique est réduite aussi. On peut faire mieux.
Pour avoir un bon échange thermique avec des gaz de combustions devenus tièdes, il faut y passer quelque chose de froid. En l'occurrence, on va y faire passer de l'air froid. Pas n'importe lequel : l'air que l'on chercher à réchauffer dans le brûler, celui qui servira de comburant dans la chaudière.
Si les gaz comburants sont déjà tièdes, c'est toujours ça qu'on n'aura pas à réchauffer avec du gaz, pour atteindre la température de fonctionnement. On a donc à nouveau fait des économies.
De plus, en réchauffant de l'air froid, on abaisse drastiquement son hygrométrie (qui dépend de la température), ce qui contribue à améliorer le rendement de la combustion.
Il y a toutefois un petit bémol : à force de refroidir des gaz de combustion, ils montent moins facilement dans la cheminée : le tirage de la cheminée est moins bon et on risque un encrassage des voies d'échappement des gaz de combustion. Un compromis et un bon réglage doivent être faits ici.
Cette seconde astuce complète la première dans l’idée de récupérer un maximum de calories de la combustion de la chaudière.
Troisième astuce
Une troisième astuce qui permet de gagner encore quelques pourcents de rendement global, c’est de chauffer moins l’eau. Ainsi, quand elle arrive en retour vers la chaudière, l’eau étant un peu plus froide, elle captera davantage de calories des gaz de combustion.
Pour des radiateurs, on ne peut pas baisser la température de l’eau : le radiateur doit pouvoir chauffer un minimum tout de même. Mais quand on a un plancher chauffant, ce dernier n’a pas besoin d’être à 60 °C : on peut se contenter de 45 °C. Le plancher chauffe globalement toute la pièce et par le bas, ce qui est une méthode très efficace pour changer une pièce.
L’eau est moins chauffée et ça utilise moins de combustible. De plus, l’eau de retour est également plus froide et l’échange thermique est meilleure là aussi.
C’est une astuce supplémentaire, mais pour l’appliquer, il faut bien-sûr réaliser quelques travaux dans la maison. Ce n’est donc pas forcément à portée de tout le monde. Mais cela reste une méthode efficace pour gagner en efficience.
Conclusion
L’appellation d’une chaudière à condensation vient de l’installation du second échangeur thermique pour réchauffer l’eau avec les gaz d’échappement. Ces gaz contiennent de la vapeur d’eau qui finissent par se liquéfier, se condenser, quand ils transmettent leur calories à l’eau du circuit de chauffage.
Cette astuce, ainsi que toutes les autres présentées ici sont destinées à récupérer le maximum de calories du gaz brûlé, par rapport à une chaudière « normale » (sans condensation), le gain peut aller jusqu’à 15 à 20 %, voire plus si vous avez une très vieille chaudière !
Il faut bien se dire que c’est une quantité d’énergie qui serait autrement perdue dans la nature et qu’ici on récupère pour chauffer notre maison. Il s’agit également d’un gain direct sur la facture, sans compter autant de gaz à effets de serre en moins. Bien sûr, le dispositif n’est rien sans un réglage convenable réalisé par un professionnel.
Heureusement, ce genre de chaudières semblent être devenues la norme aujourd’hui, ce qui limite donc les surconsommations d’énergie.